Mais il ne s'agit encore là que de procédés, sans lien entre eux, constituant un art et non une science. Pour arriver à l'étude des propriétés des figures considérées en elles-mêmes, indépendamment de toute relation avec le monde extérieur, il restait un pas difficile à franchir. Cet immense progrès, qui a eu d'incalculables conséquences dans toutes les branches de l'activité humaine, a été réalisé par le génie philosophique des Grecs; la constitution de la géométrie théorique est un des principaux mérites de ce peuple, si remarquable à bien des points de vue.

Il appartenait enfin aux Modernes de réaliser l'union intime de la géométrie et du calcul, union qui devait conduire aux importantes découvertes qui se sont succédé du XVI^e siècle au XIX^e siècle dans le domaine mathématique.

L'Orient antique

Nous savons peu de chose sur les connaissances géométriques des anciens Babyloniens en dehors des questions pratiques de dessin et d'arpentage; nous signalerons toutefois qu'ils avaient une certaine notion de la similitude et que c'est à eux qu'il convient de faire remonter la division sexagésimale de la circonférence. Les figures géométriques paraissent avoir été des symboles divinatoires.

Egypte.
S'il fallait en croire les historiens grecs, la géométrie aurait pris naissance en Egypte. En particulier, Hérodote (V^e s. av. JC) rapporte (Livre II, 409) que Sésostris 

« fit le partage des terres, assignant à chaque Egyptien une portion de  terre, et carrée, qu'on tirait au sort, à la charge néanmoins de lui payer tous les ans une certaine redevance qui composait son revenu. Si le fleuve [le Nil] enlevait à quelqu'un une partie de sa portion, il allait trouver le roi et lui exposait cequi lui était arrivé. Ce prince envoyait sur les lieux des arpenteurs pour voir de combien l'héritage était diminué, afin de ne faire payer'la redevance qu'à la proportion du fonds qui restait. Voilà, je crois, l'origine de la géométrie qui a passé de ce pays en Grèce ». 

Si l'on entend le mot géométrie dans son sens étymologique arpentage, il est hors de doute, en effet, d'après les documents qui nous sont parvenus, que les Egyptiens ont été relativement habiles dans cette voie. D'autre part, leurs harpedonaptes (tendeurs de cordeau), qui étaient chargés, d'après. un mode rituel fixé à l'avance, de procéder à l'orientation des temples suivant le méridien, employaient certains tracés pratiques que nous ignorons, mais qui étaient sans doute analogues à ceux que nous ont transmis les Çulvasûtras indiens. 

Parmi les documents: certains permettant de se faire une opinion sur le degré de culture mathématique des Egyptiens, on peut citer au premier rang le célèbre papyrus de Rhind, qui fait partie des collections du British Museum à Londres et qui a été déchiffré en 1879 par Eisenlohr. C'est un Manuel du Calculateur à l'usage des marchands et des arpenteurs, composé par un scribe nommé Ahmès, environ 1700 à 2000 ans avant notre ère, d'après des écrits plus anciens encore. La partie géométrique comprend la résolution généralement approximative de problèmes pratiques concernant le calcul de quelques aires planes et de quelques volumes simples; on y rencontre également des notions sur la similitude.

Le second document que nous ayons à citer est constitué par l'inscription hiéroglyphique du temple de Horus à Edfou (haute Egypte), qui a été signalée en 1855 par Lepsius. Cette inscription, qui date d'environ 100 ans av. JC, énumère les mesures des différentes terres qui formaient la propriété foncière du temple. Un y trouve des règles approximatives pour le calcul du triangle et du quadrilatère.

Nous signalerons enfin, en dehors des figures géométriques qu'on rencontre fréquemment sur les monuments, la connaissance que possédaient les Egyptiens du procédé dit des carrés pour agrandir ou diminuer une figure dans un rapport donné.

Grèce ancienne

Pour le surplus, on en est réduit à des conjectures basées sur des citations isolées de divers auteurs grecs ou latins.

Thalès, le précurseur. 
Le premier géomètre et philosophe grec connu est Thalès de Milet (entre 627 et 547 av. JC).  D'après Proclus, Thalès aurait énoncé les propositions suivantes :

1° Si deux droites se coupent, les angles opposés par le sommet sont égaux;

2° Dans tout triangle isocèle, les angles à la base sont égaux;

3° Un triangle est déterminé par un côté et ses deux angles , adjacents.
Eudème fait remonter ce dernier théorème à Thalès, car « il devait nécessairement s'en servir, d'après la manière dont on rapporte qu'il déterminait la distance des vaisseaux en mer »;

4° Le diamètre d'un cercle le divise en deux parties.

D'après Pamphila, compilatrice de la fin du I^er s., Thalès aurait « inscrit le triangle rectangle dans le demi-cercle ». On conclut fréquemment de ce témoignage que le Milésien devait connaître la propriété pour les angles d'un triangle d'avoir une somme égale à deux droits. Mais cette conclusion est peu vraisemblable, car Proclus attribue formellement ce théorème aux Pythagoriciens; il est plus probable que Thalès avait déduit pratiquement la propriété rappelée du triangle rectangle du fait qu'un rectangle peut être inscrit dans un cercle.

Enfin Plutarque (I^er s.) nous rapporte que Thalès ravit le roi d'Égypte par la manière dont il mesura la hauteur d'une pyramide sans aucun instrument; il aurait effectué cette mesure par la comparaison de l'ombre de la pyramide et de celle d'un bâton de longueur connue dressé verticalement, au moyen de deux triangles semblables. Or, on a tout lieu de croire que la théorie de la similitude est postérieure à Thalès; Hiéronyme de Rhodes (IV^e s. av. J.-C.) nous apprend d'ailleurs que l'opération dont il s'agit fut effectuée an moment de la journée « où l'ombre nous est égale » : il n'y a plus là qu'une notion intuitive de la proportionnalité, analogue à celle qu'on rencontre chez les Égyptiens.

En résumé - c'est l'opinion de Paul Tannery - Thalès apparait plutôt comme un chercheur de problèmes pratiques, qui a pu posséder quelques notions théoriques, mais sans les développer.

L'École pythagoricienne.
Après Thalès, le premier nom remarquable que nous ayons à signaler est celui de Pythagore (né à Samos vers 580 et est mort vers 500).  Vers 536, il aborda en Italie, à Crotone, où il fonda la célèbre école qui porte son nom. C'est incontestablement à Pythagore et, à son école que l'on doit la première impulsion véritable donnée à la géométrie, ainsi que la découverte des propositions fondamentales de cette science. Mais il est difficile de discerner ce qui revient en propre au maître et à ses disciples immédiats, car les Pythagoriciens avaient coutume de faire remonter, leurs découvertes à leur chef d'école.

En premier lieu, c'est à Pythagore qu'on devrait le fameux théorème du carré de l'hypoténuse. D'après Proclus, il aurait démontré les propositions suivantes :

1° La somme des angles d'un triangle est égale à deux droits;

2° L'assemblage de 6 triangles équilatéraux, ou de 4 carrés, ou de 3 hexagones, remplit exactement l'espace autour d'un point.

Dans le même ordre d'idées, Proclus rapporte qu'on doit à Pythagore la construction des figures du cosmos. On appelait ainsi les cinq polyèdres réguliers que les Pythagoriciens et les écoles qui en sont issues supposaient devoir être en rapport nécessaire avec le monde qui nous environne. Chez le Pythagoricien Timée de Locres (IV^e s.), par exemple, le tétraèdre représentait le feu; le cube, la terre; l'octaèdre, le vent; l'icosaèdre, l'eau ; et le dodécaèdre, l'enveloppe du monde.

La théorie de la similitude fut également étudiée avec succès dans l'école pythagoricienne, car Plutarque signale que Pythagore donna la solution du problème suivant : 

« Construire une figure équivalente à une figure donnée et semblable à  une seconde ».

Nous savons encore par Proclus que l'on doit à Pythagore l'importante découverte des nombres irrationnels : il démontra que le rapport entre l'hypoténuse et le côté d'un triangle rectangle isocèle, ou, ce qui revient au même, entre la diagonale et le côté du carré, ne pouvait être exprimé par aucun nombre connu (entier ou fractionnaire  on sait que ce rapport est représenté avec les notations actuelles par l'expression ).

En résumé, on voit qu'au moment de la dispersion des Pythagoriciens, la plupart des théories qui font l'objet de la géométrie élémentaire se trouvaient ébauchées.

Parmi les géomètres indépendants qui ne se rattachent pas à l'école pythagoricienne, nous avons à citer Oenopide de Chios (V^e s. av. JC), Hippocrate de Chios (milieu du V^e s. av. JC.) et Démocrite (460-357).

Selon Proclus, Oenopide aurait résolu les deux problèmes suivants : 

1° Abaisser d'un point donné une perpendiculaire sur une droite donnée; 

2° Construire un angle égal à un angle donné, le sommet et un côté de l'angle étant donnés. 

Hippocrate de Chios est un des plus illustres géomètres grecs. Proclus nous apprend qu'il fut le premier qui composa des Éléments (de mathématiques). Mais il s'est surtout rendu célèbre par ses études sur  les lunules qui portent son nom; l'analyse de son travail sur ce sujet par l'historien Eudème nous a été conservée par un auteur du V^e s., Simplicius. C'est vraisemblablement à notre géomètre que l'on doit le théorème relatif à la proportionnalité des aires des cercles et des carrés de leurs diamètres.

Trois problèmes fameux, dont l'étude allait être extrêmement féconde, furent posés vers le temps d'Hippocrate : la quadrature du cercle, la duplication du cube et la trisection de l'angle.

L'Académie. 
Nous arrivons à la période la plus brillante de la philosophie grecque, dont Platon (427-348 av. JC) fut un des plus illustres représentants. Après un voyage en Italie et en Sicile où il recueillit les doctrines pythagoriciennes, il fonda à Athènes la célèbre Académie, école qui devint bientôt et qui resta jusqu'à la fin de la vie de son fondateur, extrêmement florissante.

Platon était loin de partager pour les mathématiques le dédain de son maître Socrate, qui estimait suffisant de « savoir assez de géométrie pour mesurer son champ ». Proclus nous rapporte en effet que Platon « fit prendre aux mathématiques en général, à la géométrie en particulier, un essor immense, grâce au zèle qu'il déploya pour elles et dont témoignent assez ses écrits remplis de discours mathématiques et qui, à chaque instant, éveillent l'ardeur pour ces sciences chez ceux qui s'adonnent à la philosophie ». 

La tradition recueillie par un auteur byzantin du XI^e siècle de notre ère, Psellos, nous fait connaître encore que Platon aurait écrit au fronton de l'Académie :

« Que nul n'entre ici s'il n'est géomètre ».

D'après ce qu'il est possible de conjecturer, les géomètres de l'Académie ont précisé les définitions, réduit le nombre des axiomes, amélioré les démonstrations des propositions connues et mis au jour de nombreux théorèmes nouveaux. Certains d'entre eux composèrent des Éléments qui ne devaient pas différer sensiblement de ceux écrits postérieurement par Euclide.

Après Platon.
 Aristote (384-322 av. JC), disciple de Platon, avait composé un Traité de Mathématiques qui ne nous est pas parvenu. Ses élèves Théophraste (374-287) et Eudème (350-290) ont écrit chacun une Histoire de la Géométrie qui n'a pas été conservée.

Nous avons encore à signaler Archytas de Tarente (vers 430-vers 348 av. JC), philosophe et homme d'État, ami de Platon; surtout célèbre pour diverses inventions mécaniques qu'on lui attribue, il s'occupa également avec succès de la géométrie.

Eudoxe de Cnide (407-354 av. JC), qui se posa en rival de Platon, fut le fondateur de l'École de Cyzique. Il est surtout connu comme astronome, mais il a également produit de remarquables travaux géométriques. On lui doit notamment une théorie rigoureuse des proportions et nous savons par Archimède qu'il est l'auteur de démonstrations exactes de l'expression du volume de la pyramide et du cône.

D'après Proclus, Ménechme (IV^e s. av. JC), à la fois disciple de Platon et d'Eudoxe, passe pour avoir découvert les sections coniques (ellipse, parabole, hyperbole).

L'École d'Alexandrie. 
Fondée en 334 par le grand conquérant dont elle porte le nom, Alexandrie devint rapidement, sous la protection éclairée des Ptolémées, le centre intellectuel du monde antique. Les mathématiques y furent en particulier cultivées avec ardeur. C'est l'âge d'or de la géométrie grecque; dans l'espace d'un siècle environ, nous voyons se succéder ses trois plus brillants représentants: Euclide, Archimède et Apollonius.

Euclide.
Euclide enseignait à Alexandrie vers le commencement, du III^e s. av. J.-C., sous le règne de Ptolémée I^er ; il y fonda la plus célèbre école mathématique grecque. Il est surtout resté fameux pour avoir composé des Éléments où « il mit en ordre les travaux de ses devanciers et où il donna des démonstrations irréfutables pour ce que ses prédécesseurs n'avaient pas suffisamment prouvé » (Proclus). On ne sait rien de précis sur sa vie. Un géomètre du IV^e  siècle de notre ère, Pappus, nous le peint comme étant d'un naturel doux et modeste. Proclus nous rapporte d'autre part que Ptolémée, demandant un jour à Euclide s'il n'y avait pas en géométrie de route plus courte que celle des Eléments, s'attira cette réponse : 

«  Il n'y a pas en géométrie de chemin fait pour les rois. »

Indépendamment des Eléments, Euclide avait écrit diverses oeuvres de géométrie élémentaire et supérieure qui, pour la plupart, ne nous sont pas parvenues. Parmi les ouvrages qui nous ont été conservés, nous citerons le livre des Données, recueil destiné à faciliter la résolution des problèmes. Quant au livre sur le Partage des figures, on en connaît seulement un abrégé. Un écrit arabe de même titre, portant comme nom d'auteur Mahomet de Bagdad, a été découvert en 1563 par John Dee et considéré par lui comme euclidien; il en fit une traduction latine qui fut insérée dans l'édition d'Euclide de Gregory en 1703. Mais ce travail ne semble pas avoir été directement composé sur le grec et n'est sans doute qu'une imitation de l'oeuvre du géomètre alexandrin.

Enfin nous savons qu'Euclide avait encore composé les Pseudaria; il y avait « énoncé séparément et en ordre les divers genres de faux raisonnements, exerçant pour chacun notre intelligence par des théorèmes de toute sorte, où il oppose le vrai au faux, et où avec la preuve il fait concorder la réfutation de l'erreur » (Proclus).

Tels qu'ils nous ont été transmis, les Éléments comprennent 15 Livres. Les treize premiers seulement sont d'Euclide; quant aux deux autres, qui traitent des polyèdres réguliers, le XIV^e est d'Hypsiclès qui appartient au siècle suivant, et le XV^e serait dû, d'après Paul Tannery, à un géomètre byzantin du VI^e s.

• Le Livre I traite des constructions élémentaires, des cas d'égalité et des propriétés des triangles, des parallèles, de l'équivalence sous certaines conditions des triangles et des parallélogrammes, du théorème du carré de l'hypoténuse.

• Dans le Livre Il sont exposées les démonstrations géométriques de certaines relations algébriques analogues à celle qui donne le carré de la somme de deux nombres, ainsi que la résolution du problème de la division d'une droite en moyenne et extrême raison.

• Le Livre III renferme la théorie du cercle et des diverses lignes qu'on peut y considérer; c'est à peu près l'équivalent du Livre II des géométries actuelles.

• Dans le Livre IV, on étudie les figures inscrites et circonscrites à la circonférence.

• Le Livre V est entièrement consacré à la théorie des proportions.

• La similitude est présentée dans le Livre Vl à l'aide des théorèmes du Livre précédent. Un certain nombre de questions résolues aujourd'hui par la considération de triangles semblables sont traitées dans les quatre premiers Livres, sans avoir recours à cette considération, par le moyen d'artifices qui reposent souvent sur le théorème du carré de l'hypoténuse et sur les propositions du Livre ll.

• Les Livres VII, VIII et IX traitent de la théorie des nombres et le Livre X des incommensurables.

• Avec le Livre Xl, nous revenons à la géométrie; on y expose les propriétés des droites et des plans dans l'espace, des parallélépipèdes.

• Enfin, le Livre Xll s'occupe de la pyramide, du cône et du cylindre, et le Livre XIII des polygones et des polyèdres réguliers.

1° l'énoncé; 

2° l'exposé, qui est une répétition de l'énoncé où sont utilisées les lettres de la figure; 

3° la construction des lignes nécessaires à la démonstration; 

4° la démonstration;

5° la conclusion, qui est encore une répétition de l'énoncé. 

Mais il résulte pour le lecteur de cette solennelle façon de procéder une fatigue qui rend l'étude d'Euclide peu attrayante et qui est encore aggravée par ce fait que les Anciens, comme nous l'avons vu, raisonnaient sur les grandeurs elles-mêmes représentées géométriquement et non sur les nombres qui les mesurent. Ils conservaient ainsi aux raisonnements toute leur généralité, mais la lecture en était pénible par suite de la nécessité de suivre à la fois le texte et la figure; ils se privaient en outre du bénéfice de la concision que procure le calcul.

Pour la même raison, on ne rencontre pas dans les Eléments, comme dans les ouvrages actuels de géométrie, des propositions donnant d'une manière explicite l'aire des surfaces ou le volume des corps, comme par exemple celle-ci : 

« L'aire d'un parallélogramme a pour mesure le produit du nombre qui mesure sa base par le nombre qui mesure sa hauteur, lorsqu'on prend pour unité d'aire le carré construit sur l'unité de longueur ». 

« Deux parallélogrammes de même hauteur sont entre eux comme leurs bases ».

Quoi qu'il en soit, les Eléments d'Euclide constituent un modèle de rigueur scientifique atteint par bien peu d'ouvrages modernes. Ils ont été pendant vingt siècles l'ouvrage classique par excellence pour l'enseignement de la géométrie; on constate d'ailleurs actuellement une tendance générale à revenir aux méthodes d'Euclide.

Les Éléments ont été transmis aux Latins médiévaux par les Arabes. Adélard de Bath, puis Gérard de Crémone et enfin Campanus, ont donné aux XII^e et XIII^e siècles les premières traductions latines d'après l'arabe. La version de Campanus - la première qui ait été imprimée - fut publiée à Venise en 1482 par Erhard Ratdolt et souvent réimprimée depuis. La première traduction sur le grec parut à Venise en 1505 par les soins de Zamberti. 

Archimède.
Le plus grand mathématicien de l'Antiquité, Archimède (vers 287-212 av. JC), est né à Syracuse. Il est probable qu'il fit ses études à Alexandrie. Esprit profondément original, Archimède dédaigne les sentiers battus; les sujets qu'il traite n'ont jamais été étudiés avant lui et il emploie pour arriver à son but des méthodes qui lui sont propres. Ses travaux sur la géométrie élémentaire qui nous sont parvenus sont les suivants.

Dans le livre De la mesure du cercle, il établit que le rapport de la circonférence au diamètre est compris entre 3 10/71 et 3 1/7 . Le traité Sur la sphère et le cylindre comprend deux livres. Archimède y démontre en particulier : 1° que la surface d'une sphère est quadruple de celle d'un de ses grands cercles; 2° que les surfaces et les volumes de la sphère et du cylindre circonscrit sont entre eux comme 2 et 3. Un recueil de Lemmes, dont nous possédons seulement la version arabe, contient plusieurs propositions intéressantes. Enfin le grand géomètre grec est encore l'auteur d'un jeu géométrique connu sous le nom de loculus Archimedius.

Avec Archimède, la géométrie élémentaire, telle que nous la concevons aujourd'hui, est définitivement constituée. Elle comprend, en effet, la matière des Éléments d'Euclide, les mesures du cercle et de la sphère, ainsi que les propriétés des figures sphériques qui, chez les Anciens, étaient considérées comme faisant partie de l'astronomie et étaient assurément connues au temps du géomètre syracusain.

Apollonius de Perge.
Né à Perge, en Pamphilie, Apollonius, auquel les Grecs ont décerné le titre de « grand géomètre », vécut à Alexandrie vers la fin du III^e et au commencement du II^e siècle av. JC. Pappus nous dépeint son caractère sous des traits peu favorables. 

L'ouvrage capital d'Apollonius est un grand traité des Coniques en 8 livres dont 7 seulement nous ont été conservés. Il y rassemble les travaux de ses devanciers pour en faire un tout homogène, puis il expose ses propres recherches avec une profondeur de vues qui excita l'admiration des géomètres de la Renaissance, époque à laquelle on publia les premières traductions de ses oeuvres. Indépendamment des Coniques, Apollonius avait composé sur la géométrie divers autres ouvrages dont la plupart ne nous sont pas parvenus. Il avait notamment écrit deux livres perdus sur les Contacts; il y exposait la série des problèmes où il s'agit de mener des circonférences tangentes à des droites ou à des circonférences données. Ce dernier ouvrage a été reconstitué par Viète en 1600.

Nous savons-enfin, par divers passages de Proclus sur lesquels Paul Tannery a appelé l'attention, qu'il avait entrepris une revision des Éléments d'Euclide, notamment en ce qui concerne les définitions et les axiomes.

Mathématiques appliquées. 
Après cette phase si brillante de la géométrie grecque, les savants vont se tourner de préférence vers les mathématiques appliquées, vers l'astronomie surtout. Nous n'aurons plus à signaler que quelques noms remarquables

Théodose de Bithynie (I^er s. av. JC?) et Ménélas (fin du I^er s.) écrivent des ouvrages intitulés Sphériques où ils exposent les propriétés des figures tracées sur la sphère, propriétés dont les plus élémentaires étaient certainement connues avant eux.

On ne sait pas exactement à quelle époque a vécu Héron  d'Alexandrie. Il semble que le savant alexandrin est postérieur à notre ère. Héron a écrit sur les Eléments d'Euclide un commentaire dont il ne nous reste que des fragments, mais il s'est surtout créé une place à part dans le domaine, de la géométrie pratique. Dans le Traité de la Dioptre, il décrit un instrument perfectionné analogue à notre théodolite, qui servait à la fois au nivellement et au levé de plans; il y indique en outre la solution des problèmes techniques qu'on peut avoir à résoudre sur le terrain.

On savait d'autre part par Eutocius, mathématicien du VI^e siècle, que Héron avait composé un ouvrage intitulé Métriques. Les Métriques comprennent trois livres : le premier est consacré à la mesure des surfaces planes ou rondes, le second à la mesure des volumes et le troisième à des problèmes de divisions de surfaces et de volumes; les démonstrations de Héron sont bien conduites, et elles sont concises, contrairement à l'habitude des grands savants des générations antérieures.

On a enfin conservé sous la dénomination de Collection héronienne divers recueils composés probablement au X^e siècle de notre ère à Constantinople, contenant surtout des règles pratiques relatives à la mesure des surfaces et des volume. Jusque vers le milieu du XIX^e siècle, ces écrits, où les erreurs sont nombreuses, avaient bien été considérés comme byzantins, mais à la suite de la publication, en 1854, d'un remarquable mémoire de Th.-H. Martin, dont les conclusions ont été reprises et développées par Cantor dans ses Leçons sur l'Histoire des Mathématiques, on pensait qu'il ne fallait voir là que des compilations maladroites faites sur les Métriques mêmes et qu'elles constituaient le fond de ce dernier ouvrage : comme on y retrouvait la trace de l'influence égyptienne, on admettait dès lors que Héron n'avait fait que recueillir et améliorer les procédés pratiques en usage sur les bords du Nil. La publication du manuscrit de Constantinople a permis de constater que ces conclusions étaient inexactes : les Métriques constituent bien une oeuvre originale et de source entièrement grecque.

Assurément, les géodètes byzantins ont utilisé l'ouvrage de Héron, mais il se trouve aussi dans la collection pseudo-héronienne bon nombre de règles qui n'ont pas été indiquées par le géomètre alexandrin. On est donc amené à penser, contrairement à ce que l'on croyait, que les Byzantins ne se sont pas contentés de copier servilement les oeuvres des mathématiciens de l'Antiquité.

Un des plus grands astronomes grecs, Ptolémée (II^e s.), est l'auteur de la Composition mathématique, plus connue sous le nom d'Almageste; ce remarquable ouvrage, où sont exposées méthodiquement toutes, les connaissances astronomiques de l'Antiquité, contient quelques résultats géométriques intéressants, et en particulier le théorème qui exprime la relation existant entre les diagonales et les côtés du quadrilatère inscrit. Nous savons en outre que Ptolémée avait composé un livre, qui n'a pas été conservé, sur les fondements de la géométrie.

Il nous reste de Pappus, qui vécut vraisemblablement vers le commencement du IV^e s., une oeuvre importante, les Collections mathématiques en 8 livres, dont le premier et une partie du deuxième sont perdus. Indépendamment de quelques questions originales, il expose certains travaux des géomètres qui l'ont précédé; à cet égard, les Collections de Pappus sont précieuses pour se faire une idée de ceux de ces travaux qui ne nous sont pas parvenus.

Théon d'Alexandrie (fin du IV^e siècle), père de la célèbre Hypatie, donne une édition d'Euclide qui est la plus courante dans les manuscrits . il a également commenté l'Almageste.

Le célèbre philosophe néo-platonicien Proclus (412-485) est l'auteur d'un prolixe commentaire sur les Éléments d'Euclide dont il ne nous reste guère que ce qui a trait au Livre II. Ce travail ne présente d'intérêt qu'en ce qu'il a fourni la plus grande partie des renseignements que nous possédons sur l'histoire de la géométrie grecque.

Enfin Eutocius (VI^e s.) a composé sur les livres d'Archimède relatifs à la mesure du cercle, à la sphère et au cylindre et sur les Coniques d'Apollonius des commentaires sans grande valeur propre, mais précieux au point de vue historique.

La géométrie des agrimenseurs romains

« La géométrie fut chez les Grecs dans le plus grand honneur; aussi rien n'était plus brillant que leurs mathématiques. Mais chez les Romains, l'importance de cet art a été limitée à l'utilité du calcul et de la mesure. » (Cicéron. - Tusculanes, Liv. l, Chap. II).

Avant les récentes recherches sur l'âge de Héron et la publication de ses Métriques, on pensait avec Cantor que les arpenteurs romains avaient surtout puisé leurs connaissances dans les ouvrages du savant alexandrin. Actuellement, on doit rejeter cette conclusion, « non seulement parce que la tradition des agrimenseurs est antérieure à héron, mais encore parce qu'elle est nettement différente des Métriques » (P. Tannery). Leurs procédés proviendraient dès lors d'une part de source étrusque et, d'autre part, des mêmes sources grecques que celles d'où a été extraite la collection pseudo-héronienne.

Les principaux écrits des agrimenseurs Frontinus, Nipsus, Balbus, etc., composés entre le I^er et le VI^e siècle de notre ère, furent réunis pour l'enseignement dans les écoles et se conservèrent en partie intacts, mais en grande partie aussi altérés.

Ces divers écrits renferment surtout des règles se rapportant à deux questions principales : calcul de l'aire ou du volume des figures les plus simples et tracés sur le terrain. Leur étude donne une piètre idée de la science de leurs auteurs et ne présente guère d'intérêt qu'au point de vue de l'histoire de la géométrie pratique.

Cependant, vers la fin de l'Empire romain, quelques personnalités s'adonnèrent aux mathématiques théoriques. Parmi elles, nous avons un seul nom remarquable à citer, celui de Boèce (470-524). Illustre homme d'Etat, conseiller de Théodoric qui le laissa condamner et périr au milieu d'horribles supplices, il possédait un savoir encyclopédique et ses écrits lui ont assuré une grande influence pendant le Moyen âge. On lui attribue en particulier un Ars Geometria qui contient la traduction des énoncés des quatre premiers livres. des Éléments d'Euclide, ainsi que des extraits des agrimenseurs. L'authenticité de cet ouvrage, qui contient un célèbre passage relatif à l'origine de nos chiffres, a été et est encore vivement discutée.

La Chine

Les traités plus récents, écrits à une époque où l'influence hindoue et arabe avait pu se faire sentir, mais non celle des missionnaires européens, sont le Jiuzhâng Suànshù  ou les Neuf sections de l'art numérique (vers 1240) et le Suàn shù sh ou Traité complet de l'art de compter (1593); mais s'ils ne contiennent en apparence que des questions simples de géométrie pratique, leur importance dans le développement ultérieur des mathématiques, jusqu'à l'Occident même, via l'Inde et les Arabes, ne saurait être sous-estimée..

L'Inde

Leur géométrie est loin de présenter la même valeur scientitique que leur algèbre; elle porte en divers points la trace de l'influence grecque, mais aussi de l'influence chinoise. Les énoncés sont rédigés en vers d'une façon très concise, pour pouvoir être sans doute retenus plus facilement par les élèves dans les écoles; on n'y rencontre ni définitions, ni axiomes, ni démonstrations régulières. Si une preuve est jugée indispensable, l'auteur trace les lignes auxiliaires nécessaires, dispose sa figure de telle sorte que la proposition apparaisse comme évidente et il se contente de dire : « Voyez ! »; si certains problèmes relativement compliqués sont résolus, c'est en réalité par l'emploi de l'algèbre. Signalons cependant qu'il est parfois fait usage du principe de similitude.

Les plus anciens ouvrages traitant de la géométrie, qui nous aient été conservés, ont un caractère théologique. Les autels hindous devaient avoir une orientation, devaient posséder une forme prescrites à l'avance. Les règles géométriques qui permettaient de remplir ces prescriptions étaient contenues dans les Çulvasûtras ( = Règles du cordeau); plusieurs de ces recueils sont parvenus jusqu'à nous. L'auteur de l'un d'eux, Baudhâyana, semble avoir vécu aux environs de notre ère (II^e siècle d'après Cantor); il enseigne d'intéressantes constructions géométriques exécutées au moyen du cordeau.

La période classique des mathématiciens indiens commence avec Aryabhatta, né en 476 à Pâtaliputra. Son oeuvre, l'Aryabhâttiyam, est divisée en quatre sections, dont la seconde est intitulée « Eléments de Calcul »; les trois autres sections ont trait à l'astronomie. Cet ouvrage est rédigé d'une façon très laconique; on y trouve quelques règles de planimétrie et de stéréométrie dont plusieurs sont inexactes.

Brahmagupta, né en 598, écrit vers 628 un traité d'astronomie intitulé Brâhma-Sphûta-Siddhânta ( = Système de Brahma corrigé) dont les 12^e et 13^e chapitres sont relatifs aux mathématiques pures : le premier est consacré à l'arithmétique (Gânitàd'hyaya) et le second à l'algèbre (Cuttacad'hyaya). La géométrie y est considérée comme formant une division de l'arithmétique; elle consiste surtout en questions numériques concernant la mesure des surfaces et des volumes, sans démonstrations. On y trouve entre autres choses la formule donnant la surface du quadrilatère inscrit en fonction des côtés ; Brahmagupta n'a d'ailleurs envisagé que le cas particulier où les diagonales de ce quadrilatère sont perpendiculaires entre elles.

Nous n'avons ensuite à citer aucun mathématicien indien avant Bhâskara, dit Acârya ou le Savant, né en 1114; il est l'auteur du Siddhântaçiromaji ( = Couronnement, du système), grand traité d'astronomie qui renferme deux sections portant comme titres particuliers Lîlâvati (la charmante - nom de la fille de Bhâskara - traite de l'arithmétique et le Vîja-ganita est consacré plus particulièrement à l'algèbre. La géométrie est surtout exposée dans la première section, avec plus de prolixité que chez Brahmagupta; indépendamment des problèmes sur la mesure des surfaces et des volumes, on y rencontre d'assez nombreuses questions sur les triangles rectangles, avec quelques démonstrations.

Après Bhâskara, on ne trouve plus que des commentateurs qui, jusqu'au XVII^e siècle, annotent ses oeuvres sans toujours les bien comprendre; la science indienne s'éteint rapidement.

La géométrie des Arabes

Cette période est la plus remarquable de la mathématique arabe. Mohammed ben Moussa al-Khwârizmi publie vers l'an 820 le premier ouvrage connu sur l'algèbre et dont le titre, corrompu, a donné son nom à cette science (Abrégé pour le calcul par Djebr el-Mokâbalah). Cet ouvrage, d'une importance capitale au point de vue historique, fut composé à la demande d'al-Mamoun pour les besoins de la vie courante; il contient un chapitre sur la géométrie de mesure. Khwarizmi avait aussi composé, vraisemblablement avec ses deux frères, Ahmed et al-Hasan, un écrit géométrique qui fut traduit en latin sous le titre Liber trium fratrum de geometria.

Un des plus célèbres astronomes arabes, Aboûl Wafâ (940-998), est l'auteur d'un excellent Recueil de constructions géométriques. Mahomet de Bagdad (X^e siècle) compose un Traité sur la division des surfaces, calqué sur l'oeuvre d'Euclide traitant du même sujet, et Hassan ben Haitham écrit (vers l'an 1009) un Traité des connues géométriques analogue aux Données du géomètre grec. Enfin Nassir ed-Din (1201-1274) nous a laissé un intéressant commentaire des Éléments d'Euclide.

A partir du XIII^e siècle, les mathématiques sont en pleine décadence en Orient. Dans l'école espagnole, dont l'importance est loin d'atteindre celle de l'école de Bagdad, nous n'avons à signaler aucun nom remarquable.

L'Occident latin au Moyen âge

Les notions scientifiques tout à fait rudimentaires qu'on possède sont conservées dans les monastères. Les trois esprits les plus remarquables de cette période de ténèbres, les Anglo-Saxons Bède et Alcuin, et le Français Gerbert, sont des ecclésiastiques.

Bède.
Bède (672-735) a composé un grand nombre d'écrits, dont quelques-uns relatifs à l'arithmétique, à la géométrie et à l'astronomie. On lui a attribué des Propositiones ad acuendos juvenes (Propositions pour aiguiser la perspicacité des jeunes gens), recueil de problèmes qui a probablement été le germe des ouvrages postérieurs sur les récréations mathématiques et qui contient quelques questions de géométrie pratique ; mais certains indices font supposer que l'auteur de cet ouvrage est plus vraisemblablement Alcuin.

Alcuin.
Le précepteur et l'ami de Charlemagne, Alcuin (735-504), qui fut aussi disciple de Bède, eut une influence considérable sur ses contemporains. Il s'efforça de développer le goût de l'étude chez les moines et créa de nombreuses écoles auprès des cloîtres et des cathédrales.

Gerbert.
Mais celui qui peut véritablement prétendre au titre de restaurateur des sciences en Occident est Gerbert (vers 930-1003). Originaire d'Auvergne, il entra dans les ordres, alla s'instruire en Espagne, devint par la suite archevêque de Reims, puis de Ravenne et enfin pape sous le nom de Sylvestre Il. Il composa divers écrits mathématiques, notamment un Libellus Geometriae qui ne nous est pas parvenu. On possède sous son nom, bien qu'il rie paraisse pas en être l'auteur, une Geometria qui comprend trois parties distinctes dues vraisemblablement à des auteurs différents. La première partie, la plus originale, est un essai inachevé d'une exposition méthodique de la géométrie; dans la deuxième sont résolus divers problèmes d'arithmétique ; la troisième enfin a pour objet le calcul des longueurs, des surfaces et des volumes. Le noyau de cette dernière partie a peut-être été formé par le Libellus mentionné ci-dessus.

Influence arabe  (XIII^e - milieu du XV^e s.).
Pendant le XI^e siècle, l'impulsion imprimée par Gerbert subit un temps d'arrêt, et il faut arriver au commencement du XII^e siècle pourvoir un véritable courant scientifique se dessiner sous l'influence des Arabes d'Espagne. Adélard de Bath (vers 1115) et Gérard de Crémone (1144-1187) traduisent les Eléments d'Euclide d'après les versions arabes.

Fibonacci.
Vers le début du XIII^e siècle apparaissent les oeuvres du grand mathématicien du Moyen âge, Léonard de Pise dit Fibonacci. Après avoir vécu à Bejaïa (Algérie) où son père était l'acteur au comptoir pisan, il voyage en Orient et revient à Pise. Il y écrit en 1202 son fameux Liber Abaci, qui contient une exposition originale des connaissances arabes en arithmétique et en algèbre, et qui constituera le fond des écrits des mathématiciens de la Renaissance.

Indépendamment du Liber Abaci et de travaux algébriques importants, Fibonacci compose encore une Practica Geometria publiée en 1220. Cet ouvrage renferme tout ce qui est contenu dans Euclide et Archimède sur la mesure des surfaces et des volumes; on y trouve en outre la division des figures planes dans un rapport donné, divers procédés d'arpentage et la partie élémentaire de la trigonométrie. Les données des problèmes sont numériques; les démonstrations, où il est fait usage de l'algèbre, sont rigoureuses et présentées d'une façon très claire. En résumé, Léonard de Pise est un véritable mathématicien, supérieur à tous ceux qui l'ont précédé et suivi au Moyen âge. Ses travaux ne se propagèrent néanmoins qu'avec une extrême lenteur.

Après lui, nous n'aurons plus à signaler que quelques esprits éminents qui, dans un milieu plus propice, eussent assurément pu fournir des productions présentant plus d'intérêt.

Jordanus Nemoranius.
Un des hommes qui eurent le plus d'influence sur le développement intellectuel à la fin du Moyen âge fut Jordanus Nemoranius ou Jordanus de Saxe, qui fut élu en 1222 général des Dominicains, ordre se consacrant à l'enseignement. Les divers écrits mathématiques, non sans valeur, qu'il composa se répandirent rapidement dans les écoles et furent longtemps réédités et commentés; l'autorité qu'il exerça sur ses contemporains fut d'ailleurs une des causes qui rendirent difficile la diffusion des ouvrages de Fibonacci dans les Universités. On doit notamment à Jordanus un ouvrage estimable, De Triangulis, divisé en quatre livres. Dans les deux premiers, il traite des figures rectilignes dans les deux derniers, du cercle et des lignes qui sont avec lui en rapport étroit; le second livre est en particulier consacré à la division des figures.

De Campanus de Novare à Nicolas de Cues.
Peu après, nous devons placer Campanus de Novare (fin du XIII^e siècle), surtout connu pour être l'auteur de la première traduction latine des Éléments d'Euclide qui ait été imprimée. Signalons aussi en passant un Traité de Géométrie anonyme, composé sous le règne de Philippe le Hardi (1270-1285). Le mérite essentiel de cet opuscule est d'être le premier travail de ce genre écrit en français; on y donne quelques règles de planimétrie et de stéréométrie. Citons enfin dans le même ordre d'idées que ce dernier traité, l'intéressante Practica Geometria de Dominicus de Clavasio (ou Dominicus parisiensis), mathématicien éminent pour son temps, qui fut astrologue à la cour de France dans la seconde moitié du XIV^e siècle.

Nous revenons maintenant au monde ecclésiastique. Bradwardine (1290-1348), qui fut archevêque de Canterbury, a laissé une Geometria speculativa qui contient d'intéressantes propositions sur les polygones étoilés et les figures isopérimétriques. Le plus remarquable des successeurs de Fibonacci, Nicole Oresme, mourut évêque de Lisieux en 1382; il a notamment exposé, dans son Tractatus de latiludinibus formarum, le principe du procédé retrouvé plus tard par Descartes pour représenter graphiquement la relation existant entre deux quantités variables au moyen d'une ordonnée (latitude) et d'une abscisse (longitude). Enfin, le cardinal Nicolas de Cues (1401-1464), qui encouragea les mathématiques, est resté célèbre pour ses nombreux essais de quadrature du cercle.

Les Modernes

Parmi les traducteurs les plus célèbres, nous citerons l'astronome allemand Müller dit Regiomontanus (1436-1476), qui dirigeait lui-même à Nuremberg l'imprimerie où furent exécutées de très belles éditions des mathématiciens grecs. Le Sicilien Maurolycus (1494-1575) a laissé, indépendamment de ses propres recherches, une traduction des Coniques d'Apollonius et une intéressante paraphrase d'Archimède. Mais c'est surtout à l'Italien Commandino (1509-1575) que l'Europe est redevable de précieuses traductions des géomètres alexandrins, éclairées par de remarquables commentaires.

Toutefois, la véritable caractéristique de cette période réside en ce fait que l'union entre la géométrie et l'algèbre, ébauchée par les Indiens, les Arabes et les savants du Moyen âge, va devenir de plus en plus intime et aboutir au XVII^e siècle à la création de la géométrie analytique et du calcul infinitésimal.

Paciuolo.
En 1494, paraît la Summa de Arithmetica, Geometria, Proportioni et Proportionalita du franciscain italien Luca Paciuolo, connu encore sous le nom de Lucas de Burgo (1445-mort après 1514). Cet ouvrage se divise en deux sections, l'une relative à l'arithmétique et à l'algèbre, l'autre à la géométrie. La dernière comprend huit parties, traitant de la mesure des surfaces et des volumes, de la division des figures et de diverses questions d'arpentage; les problèmes géométriques sont souvent résolus avec le secours de l'algèbre, sur des données numériques. On constate dans la Summa de nombreux emprunts aux écrits de Fibonacci, dont les travaux se trouvèrent ainsi portés à la connaissance des géomètres; mais la copie est inférieure au modèle tant par la forme que par le fond. Tel quel, cet ouvrage a néanmoins contribué puissamment au progrès des mathématiques au XVI^e siècle. Paciuolo est encore l'auteur d'un curieux ouvrage intitulé De divina proportione (1509), où il expose de nombreuses applications aux arts de la division d'une droite en moyenne et extrême raison.

Cardan et Tartaglia.
De même que Paciuolo, les mathématiciens de la Renaissance font constamment usage de l'algèbre en géométrie, et inversement. On le constate en particulier chez les savants italiens Cardan (1501-1576) et Tartaglia (1505-1557), auxquels l'algèbre doit de notables progrès et dont les démêlés sont restés célèbres. L'oeuvre principale de Tartaglia, General Trattato di numeri et misure (1556-1560), est divisée en six parties dont les quatre dernières, consacrées à la géométrie, renferment d'intéressants problèmes; on lui reproche toutefois de contenir beaucoup d'incorrections.

Viète.
Nous arrivons ainsi à François Viète (1540-1603), qui crée l'algèbre littérale et va permettre ainsi de réaliser l'union complète de la géométrie et de l'algèbre. Jusque-là, en effet, comme nous avons eu occasion de le signaler; les démonstrations géométriques présentées sous forme algébrique étaient basées sur les données numériques, et il ne pouvait en être autrement puisque l'algèbre était une science exclusivement numérique. Le raisonnement gagnait en commodité et en rapidité, mais il perdait en même temps la généralité que nous avons rencontrée chez les Grecs. L'emploi de symboles permettait de conserver à la géométrie ce dernier caractère, tout en lui gardant les avantages du calcul.

Viète ne se contente pas de créer l'algèbre moderne; il l'applique à la géométrie. Il entreprend d'une manière systématique, notamment dans ses Effectiones geometricae (1593) et dans son Supplementum Geometriae (1593), la résolution algébrique des problèmes géométriques en même temps que la construction géométrique des formules algébriques. On doit encore à Viète, dans un ordre d'idées différent, la reconstitution de l'ouvrage perdu d'Apollonius, Des Contacts, qu'il publie en 1600 sous le pseudonyme d'Apollonius Gallus; il y résout le problème, difficile pour son temps, de mener une circonférence tangente à trois circonférences données.

Kepler.
Signalons encore comme travaux d'application de l'algèbre à la géométrie les remarquables aperçus de Kepler (1571-1631) sur les polygones étoilés dans son immortel ouvrage Harmonices Mundi (1619). On doit aussi à Kepler la grande innovation qu'a été sa formulation du principe de continuité géométrique. La notion d'infini qu'elle impliquait permettait des généralisations et des systématisations jusque-là inimaginables; et la méthode de division indéfinie appliquée à la rectification, et les problèmes de quadrature et de cubature évitaient la méthode encombrante d'épuisement et fournissaient des résultats plus précis.

De Vinci à Stévin.
Durant la Renaissance, les mathématiciens italiens se passionnent littéralement au sujet des constructions géométriques exécutées avec une ouverture de compas constante.

On s'occupe également des tracés géométriques approchés. Nous citerons sur ce point : Léonard de Vinci (1452-1519), qui a indiqué dans ses manuscrits nombre de constructions approximatives niais paraissant avoir été tenues par lui pour exactes; un opuscule anonyme de la fin du XV^e siècle, la Geometria deutsch; et un intéressant ouvrage d'Albrecht Dürer intitulé Underweysung der messung mit dem zirkel und richscheyt ( = Instruction sur le mesurage avec le compas et la règle) (1525). Mais à la différence de Vinci, Dürer sait que ses tracés ne sont pas rigoureux.

Enfin, on publie à la même époque de nombreux écrits sur la géométrie pratique, parmi lesquels nous signalerons l'excellent ouvrage du jésuite Clavius (1537-1612), connu aussi pour une bonne édition des Eléments d'Euclide, et celui de Simon Stévin (1548-1620).

Le XVII^e.
Avec le XVII^e siècle, commence une ère nouvelle dans l'histoire des mathématiques.
De nouveaux progrès ont été réalisés par Cavalieri, qui, dans son Continuorum indivisibilibus géométrique (1620), a conçu une méthode intermédiaire entre celle de l'épuisement et le calcul infinitésimal de Leibniz et Newton. La base logique de son système a été corrigée par Roberval et Pascal ; et leurs découvertes, prises en conjonction avec celles de Leibniz, Newton et bien d'autres, ont abouti à la branche de notre sujet connue sous le nom de géométrie différentielle.

Une deuxième avancée importante a suivi la reconnaissance que les coniques pouvaient être considérées comme des projections d'un cercle, une conception qui a conduit, entre les mains de Desargues et Pascal, à la géométrie et à la perspective projectives modernes. 

Une troisième avancée, et peut-être la plus importante, fut l'application de l'algèbre à la géométrie par Descartes, qui fonda ainsi la géométrie analytique (1637). 

En ce qui concerne plus particulièrement la géométrie élémentaire, nous n'avons rien d'important à signaler jusqu'à la fin du XVIII^e siècle. Les seuls travaux originaux composés durant cette période et dont il mérite d'être parlé sont le Cours mathématique de Pierre Hérigone (première moitié du XVII^e siècle), publié en 1644, et la Characteristica Geometria de Leibniz (1616-1716), composée en 1679, mais non publiée à l'époque. Ces deux ouvrages, où sont exposées des notations destinées à simplifier le langage et à faciliter le raisonnement en géométrie, sont les premiers essais connus de ce qu'on nomme aujourd'hui la « Logique mathématique ».

Les traités de géométrie en France au XVII^e siècle.  - Jusqu'au milieu du XVII^e siècle, la géométrie théorique est exclusivement enseignée au moyen des Éléments d'Euclide sous leur forme primitive, c'est-à-dire par l'emploi de démonstrations exclusivement géométriques. Parallèlement aux éditions de l'oeu vre du savant grec, on publie de nombreux ouvrages dits de géométrie pratique, où, à côté de certaines questions qui ne se trouvent pas dans les Éléments, comme par exemple la mesure du cercle, sont exposés des problèmes numériques sur la planimétrie et la stéréométrie.

Ce fut le célèbre Antoine Arnauld (1612-1692), l'un des auteurs de la Logique de Port-Royal, qui, en France, porta le premier coup à l'autorité jusque-là incontestée d'Euclide, en publiant en 1667 ses Nouveaux Elemens de Geometrie. 

« Il n'estoit pas fort difficile à l'auteur de la nouvelle Logique ou Art de penser, dit Nicole qui a écrit la préface dé l'ouvrage, de remarquer... les défauts de la méthode d'Euclide et d'avancer qu'on pourroit digérer la géométrie dans un meilleur ordre. »

Arnauld expose donc les matières de la géométrie plane des Éléments dans un ordre différent de celui du géomètre grec, mais à peu près pareil à celui qui sera suivi ensuite; il faut bien dire qu'il n'est pas toujours heureux en essayant de réformer Euclide. Son ouvrage est surtout caractérisé par l'introduction des démonstrations algébriques partout où cela est possible; en outre, on n'y trouve plus ces fatigantes répétitions de l'énoncé que nous avons signalées chez les Anciens; il est ainsi beaucoup plus facile à lire que les Eléments et restera longtemps le modèle suivi par les auteurs postérieurs.

En 1685, le R.-P. Bernard Lamy (1610-1715), prêtre de l'Oratoire, publie des Elemens de Géometrie conçus d'après le même plan que ceux d'Arnauld; ils contiennent en outre ce que nous appelons aujourd'hui la géométrie de l'espace, ainsi que la mesure du cercle, sauf toutefois la détermination de pi. Ce petit ouvrage, clair et concis, a été très estimé en son temps.

Vers la fin du XVII^e siècle, nous avons à mentionner la Géométrie élémentaire et pratique de Sauveur (1653-1716), rééditée en 1753 par Le Blond. La disposition est encore calquée sur celle d'Arnauld, mais nous voyons apparaître pour la première fois des énoncés pratiques pour la mesure des surfaces et des volumes, comme celui-ci: 

« L'aire d'un cercle est égale à la moitié du produit de sa circonférence par son rayon»

Toutefois, les démonstrations qu'il donne des propositions correspondant à ces énoncés, et qu'il base sur la doctrine des indivisibles, sont loin d'être rigoureuses.

Les traités de géométrie en France au XVIII^e siècle. - Nous signalerons ici la partie géométrique des Elémens de Mathématiques de Varignon (1651-1722), publiés en 1731, qui contient quelques intéressantes constructions approchées, et les Élémens de Géométrie de Clairaut (1743-1765), parus en 1741, où l'auteur, sous une forme excellente, cherche à rendre l'étude de cette science plus attrayante en faisant découler les vérités géométriques des faits sensibles. Enfin, en 1794, paraissent les remarquables Éléments de Géométrie de Legendre (1752-1833) qui, dès leur apparition, eurent un succès considérable; ils sont restés classiques pendant plus d'un siècle et forment encore aujourd'hui en France la base des ouvrages de géométrie élémentaire. Legendre y expose dans le même ordre qu'aujourd'hui la matière des Éléments d'Euclide, la planimétrie et la stéréométrie avec des énoncés pratiques, la mesure du cercle avec la détermination de pi; il y introduit enfin les propriétés des triangles sphériques. Il se montre beaucoup plus rigoureux que ses devanciers, bien qu'il ne réussisse pas toujours dans ses essais de réduction du nombre des principes admis par les géomètres grecs. On lui a reproché d'avoir eu trop souvent recours aux démonstrations par l'absurde, mais c'était une conséquence même de la condition qu'il s'était imposée de ne pas employer, la méthode des limites, jugée par lui comme n'étant pas assez simple pour être introduite dans un ouvrage de cette nature. Avec Legendre, la géométrie élémentaire est définitivement constituée sous sa forme actuelle; ses successeurs ne feront que modifier certains points de détail.

Le XIX^e siècle

Monge n'a pas limité ses travaux à la géométrie descriptive; il a exposé le théorème fondamental des polaires réciproques, mais pas en langage moderne, a donné un traitement des surfaces réglées et a étendu la théorie des polaires aux quadriques. Monge et son école s'occupaient surtout de la théorie de la forme, mais Desargues, Pascal et Carnot traitaient surtout des relations métriques des figures. Carnot a étudié ces relations en particulier liées à la théorie des transversales, dans ses ouvrages, Géométrie de position (1803), Théorie des transversales (1806). Sa géométrie de position actuelle a peu de choses en commun avec la géométrie de position de Carnot.

La géométrie du triangle.
A partir de 1873, la « géométrie du triangle » a été l'objet d'importants travaux de la part de nombreux géomètres, au premier rang desquels il convient de citer : en France E. Lemoine et H. Brocard, en Belgique J. Neuberg.

Géométrie projective.
Bien que Newton ait découvert que toutes les courbes du troisième ordre peuvent être dérivées par projection centrale à partir de cinq types fondamentaux, l'origine de la géométrie projective se rencontre chez Gérard Desargues, Blaise Pascal, Gaspard Monge et Lazare Carnot, mais c'est surtout au nom de Jean Victor Poncelet (1822), le créateur des méthodes modernes, que sa fondation doit être attachée. Dans son Traité des propriétés des figures (1822) la ligne et les points circulaires à l'infini, les imaginaires, la réciprocité polaire, l'homologie, le birapport et la projection sont systématiquement employés. On doit ainsi à Poncelet d'avoir mis en évidence la puissance des relations projectives, et le principe de continuité dans la recherche. 

August Möbius a suivi Poncelet, faisant beaucoup usage des rapports anharmoniques dans son Barycentrischer Calcul (1827), où il a introduit les coordonnées homogènes, ainsi que la puissante notion de transformation géométrique, y compris les cas particuliers de colinéation et de dualité.

Les propriétés de point et de ligne anharmoniques des coniques ont été élaborées plus en détail par Michel Chasles, Karl von Staudt,  Steiner et Brianchon (1806), qui prolonge l'application de la théorie des polaires de Desargues. 

L'introduction de la droite comme élément d'espace, initiée par H. Grassmann (1844) et Cayley (1859), ont donné aux mains de Plücker une nouvelle géométrie, appelée géométrie linéaire / algèbre linéaire. Julius Plücker, dans son Analytischgeometrische Entwickelungen (1828-1831) et son System der analytischen Geometric (1835), a ainsi introduit la notation abrégée, les coordonnées de ligne et de plan, et la conception d'éléments spatiaux généralisés; il a en outre appliqué la théorie des transversales aux courbes. Ces questions ont été développée plus particulièrement par Felix Klein, Rudolf Clebsch, C. T. Reye et F. O. R. Sturm.

La géométrie analytique a été stimulée par l'algèbre des invariants, sujet très développé par A. Cayley, G. Salmon qui a découvert les points dits circulaires à l'infini, S. H. Aronhold, L. O. Hesse, et plus particulièrement par Clebsch.

C'est à Joseph Gergonne (1825-1826) que l'on doit le principe de dualité, le plus important après celui de continuité dans la géométrie moderne. Gergonne a été la première à utiliser le mot « classe », et à définir explicitement classe et degré (ordre), montrant leur double relation. Lui et Chasles ont été les premiers à étudier scientifiquement les surfaces d'ordre supérieur. 

Jakob Steiner (1832), en plus d'enrichir la géométrie dans de nombreuses directions, a donné la première discussion complète des relations  concernant les faisceaux projectifs, et a jeté les bases de la géométrie pure moderne. 

En 1848, Steiner a montré que la théorie des polaires peut servir de base à l'étude des courbes planes, indépendamment de l'utilisation des coordonnées. Il a introduit les courbes remarquables qui portent maintenant les noms de lui-même Hesse et Cayley. Chasles, dans son Aperçu historique (1837), popularisa la nouvelle géométrie et introduisit le nom homographique, et étendit la théorie homographique. 

La géométrie synthétique.
La géométrie synthétique (géométrie axiomatique), caractérisée par sa fécondité et sa beauté, a attiré le plus l'attention, et il se trouve que ses fondements logiques initialement faibles ont été remplacés par un ensemble plus substantiel d'axiomes. Celles-ci ont été trouvées dans le rapport anharmonique, un dispositif conduisant à la libération de la géométrie synthétique des relations métriques, et dans l'involution, qui a donné des définitions rigoureuses des imaginaires. Ces innovations ont été faites par K. J. C. von Staudt (1847, 1856-1860), qui a proposé un système géométrique pur et complet dans lequel la géométrie métrique n'a pas sa place. Cremona (1862, 1875), Townsend (1863) et Clifford ont beaucoup fait pour étendre la connaissance de la géométrie moderne.
-
Les géométries non-euclidiennes.
Au XIX^e siècle, les mathématiciens ont également porté leurs efforts sur l'étude fondements de la géométrie et plus spécialement sur l'examen des axiomes qui servent de base à la géométrie, ce qui a débouché sur le développement des géométries non-euclidiennes. 

Ces géométries ont principalement leur origine dans la discussion des parallèles euclidiens, et traitées par Wallis, Saccheri et Lambert, se sont surtout développées au cours du XIX^e siècle. Quatre axes de recherche peuvent être distingués : 1°) celui associé à Lobatschevski, Bolyai, Gauss; 2°) celui étudié par Riemann, Helmholtz, Beltrami; 3°) celui développé par Cayley, Klein, Clifford; et 4°) celui promu principalement par Peano, Veronese, Burali-Forte, Levi Civita, Pasch et Hilbert. (E. Fourrey; C.E. / EB).

La géométrie consiste en un ensemble de démonstrations absolument rigoureuses, si l'on admet, en dehors de définitions purement verbales, un certain nombre de propositions primordiales que l'on qualifie d'axiomes ou de postulats. Les énoncés de ces propositions ont d'ailleurs un caractère complètement abstrait, en sorte qu'elles paraissent, à première vue, appartenir à un autre domaine que celui de l'expérience; il est clair cependant qu'à ce point de vue la géométrie n'a pas eu jusqu'à une époque relativement récente le même degré d'indépendance que l'arithmétique (entendue au sens universel); les objets de cette dernière, expliquait-on, peuvent être conçus avec l'aide du sens intérieur seul, ceux de la première sont nécessairement succeptibles d'être perçus sous le mode concret, par le sens extérieur. Mais si celui-ci, comme le dit Kant, a l'espace pour forme a priori, l'intellect n'est-il pas par là même obligé à reconnaître, comme également a priori, les conditions propres de cette forme? La constitution de la géométrie imaginaire a prouvé aux mathématiciens et aux philosophes que cette obligation n'existe pas pour tous les axiomes. Ce qui fait dire à Paul Tannery : 

[Ces axiomes] « reposent donc sur l'expérience; seulement il ne s'agit pas ici de l'expérience telle qu'on l'entend en physique, entreprise sur des phénomènes particuliers pour en déterminer les lois inconnues, mais de l'expérience générale qui donne successivement à tous les hommes un même enseignement et, probablement après une longue série de générations, est ainsi parvenu à leur inculquer la ferme croyance à des relations abstraites qu'ils qualifient de vérités d'intuition. D'un autre côté, si le point de départ de la géométrie est expérimental (par conséquent contingent et pouvant dès lors n'être pas soit rigoureusement, soit absolument vrai), la science n'en est pas moins indépendante de l'expérience, du moment où elle ne prend les postulats que comme hypothèses, et n'a pas dès lors à s'occuper de la vérification de ses conclusions. Il va sans dire que, pour les applications de la science aux objets concrets, la situation n'est pas la même; mais il est suffisamment connu par la pratique que les imperfections des instruments et des moyens de mesure sont telles que les discordances entre les calculs et les observations doivent toujours être mises à leur compte.

Pour préciser davantage le rôle de l'expérience dans la constitution des axiomes, prenons d'abord celui dont l'intuition parait la moins nécessitée, celui qui est connu sous le nom de postulatum d'Euclide, que par un point on ne peut mener, dans un plan, qu'une seule, droite qui soit parallèle à une autre (qui ne la rencontre pas). Nous remarquerons que ce n'est pas évidemment sous cette forme que ce postulat est enseigné par l'expérience générale ni qu'il pourrait être vérifié par l'expérience particulière. S'il était réellement en question, on s'attacherait à l'une des conséquences que l'on en tire : on mesurerait les trois angles d'un triangle très grand et on s'assurerait si leur somme fait ou non deux droits, procédé qu'au reste Gauss et Legendre n'ont pas jugé hors de propos de discuter sérieusement. Quant à l'expérience générale, ce qu'elle enseigne effectivement, c'est d'autres conséquences, par exemple la constance des rapports entre les côtés de triangles dont les angles sont les mêmes. Il est clair que, dès que l'on a commencé, pour les besoins de l'architecture, à faire du dessin géométrique, cette constance a été postulée et que si on prend un ouvrier intelligent, mais non instruit, il sera plus facile de lui faire comprendre le principe de l'échelle dans un dessin que la formule abstraite du postulatum. Enfin il est établi  qu'il est possible de construire, sans aboutir à aucune contradiction, un système complet de géométrie où l'on suppose que, par un point, on peut dans un plan mener une infinité de droites qui ne rencontrent pas une droite donnée du plan.

Prenons au contraire la notion qui est au fond de toute intuition et qu'on exprime sous une formule plus commode que vraiment scientifique, en disant que l'espace a trois dimensions. Il est certain que l'enfant acquiert de lui-même cette notion par le fonctionnement naturel de ses sens, et l'on peut d'autant moins dire qu'elle est donnée a  priori, qu'on ne peut en donner aucune raison suffisante. Rien n'est d'ailleurs plus facile que de constituer, sans contradiction, une géométrie à plus de trois dimensions; mais, comme elle ne se prête pas à l'intuition, cette prétendue géométrie ne sera, à vrai dire, qu'une combinaison logique de symboles analytiques. Ainsi tous les axiomes de la géométrie sont empruntés à l'expérience, mais ils se présentent à nous comme plus ou moins indispensables à l'intuition, sans qu'il y ait d'ailleurs intérêt réel à les classer rigoureusement à cet égard. » 

L'espace, dans ces théories, n'a plus rien de commun avec l'espace physique; c'est un pur objet de la pensée, une multiplicité à plusieurs entrées; les premiers travaux sur ce sujet ont été exclusivement conçus dans l'hypothèse de la continuité (divisibilité indéfinie); mais on a très vite envisagé d'examiner celle de la discontinuité. La géométrie à plusieurs dimensions a le plus souvent été développée comme généralisation analytique et on y a été naturellement conduit par l'analogie des formules de la géométrie plane et de celle de l'espace; mais on doit remarquer que les espaces à trois dimensions de la géométrie euclidienne, de celle de Riemann et de celle de Lobatchevski jouent, par rapport à l'espace euclidien à quatre dimensions, le rôle de surfaces différentes de notre géométrie ordinaire. La géométrie à plusieurs dimensions forme donc en réalité le cadre général de la géométrie imaginaire. On a essayé de l'étendre en concevant des nombres fractionnaires de dimension.

Géométries euclidienne et non-euclidienne.
La géométrie prend comme point de départ de ses déductions un certain nombre de postulats (axiomes) fournis éventuellement par  l'expérience la plus générale  et qui, comme tels, sont souvent regardés comme évidents par eux-mêmes. On peut énumérer et formuler ces postulats de diverses façons ; en tous cas, ce sont ceux qui se trouvent implicitement ou explicitement admis dans l'ouvrage classique le plus ancien, les Éléments d'Euclide. Dès cette époque, en effet, l'ensemble des postulats nécessaires à la constitution de la science est définitivement arrêté et, d'un autre côté, tous ceux qui avaient pu être admis antérieurement, mais étaient susceptibles d'être démontrés (c.-à-d. déduits de l'ensemble des autres) se trouvent ramenés au rang de théorèmes. Nous pouvons considérer au reste tous les postulats des Éléments comme absolument rigoureux, car lest bien certain que pratiquement les conséquences d'aucun d'entre eux ne seront jamais contredites par notre expérience; mais, par cela même qu'ils sont fondés a posteriori et non pas a priori, nous pouvons aussi concevoir l'hypothèse où tel d'entre eux ne serait pas exact et où on lui substituerait un postulat différent, mais plus général, et comprenant le postulat usuel comme cas particulier. Si on développe les conséquences de cette hypothèse, on constituera une théorie, d'importance purement abstraite, que l'on appellera géométrie non-euclidienne par opposition à la géométrie usuelle ou euclidienne. Ces dénominations sont dues à Gauss qui, dès 1792, avait en particulier envisagé ce qui résulterait de la supposition de la fausseté de la proposition que par un point on ne peut mener qu'une seule parallèle, à une droite, proposition qui, comme on sait, est généralement connue sous le terme de postulatum d'Euclide.

Gauss ne publia rien de ses travaux à ce sujet; les premiers mémoires de géométrie non-euclidienne sont dus à Johann Bolyai qui employa d'ailleurs le terme de Science de l'espace absolument vraie (1832) et à Nicolas Ivanovitch Lobatchevski qui adopta d'abord celui, assez malheureux, de géométrie imaginaire (1835 à 1838), puis un autre, Pangéométrie (1855). Dans ces mémoires, l'hypothèse fondamentale est la suivante : Dans le plan défini par une droite AB et un point extérieur C, on peut mener par C une infinité de droites ne rencontrant pas AB; ces droites seront toutes comprises dans les angles aigus et opposés par le sommet que forment deux droites symétriques par rapport à la parallèle d'Euclide et qui sont appelées parallèles à la droite AB. Ces droites sont regardées, l'une pour le côté A, l'autre pour le côté B, comme les limites des droites menées de C à la droite AB et dont le point d'intersection s'éloigne à l'infini. L'angle de parallélisme u, c.-à-d. l'angle aigu formé par une parallèle à AB avec la perpendiculaire abaissée de C sur AB, varie avec la longueur a de cette perpendiculaire ; on démontre la relation :

dans laquelle k est un paramètre à déterminer arbitrairement ou par l'expérience. Pour la géométrie euclidienne, ce paramètre est plus grand que toute quantité donnée.

Pour énoncer les principaux résultats de l'hypothèse de Gauss, je désignerai, avec Bolyai, par système S celui de la géométrie non-euclidienne, par système  celui de la géométrie euclidienne. La géométrie de la sphère est identique dans les deux systèmes tant que le rayon n'est pas considéré. Dans le système , une circonférence de cercle dont le centre s'éloigne à l'infini sur la perpendiculaire à une droite tangente, a pour limite cette tangente; dans le système S, cette limite est une courbe distincte, horicycle; de même la limite d'une surface sphérique, dont le centre s'éloigne à l'infini sur la perpendiculaire à un plan tangent, n'est pas ce plan, mais une surface de révolution, l'horisphère, ayant pour méridienne un horicycle. Il n'y a dans un plan du système  que deux lignes uniformes, c.-à-d.  telles qu'une partie quelconque puisse parcourir la ligne tout entière sans déformation; ce sont la ligne droite et le cercle; dans le système S, il y a, en outre, comme lignes uniformes, l'horicycle et les courbes parallèles à une droite (lieux des extrémités de perpendiculaires de même longueur élevées en différents points et du même côté d'une droite). De même dans l'espace, il y a quatre surfaces uniformes: le plan, la sphère, l'horisphère et les surfaces courbes parallèles à des plans. Toute propriété établie dans le système  entre droites sur un plan est vraie dans le système S entre horicycles sur une horisphère. Les relations métriques les plus ordinaires sur le plan dans le système  ne sont pas conservées dans le système S. Les formules de planimétrie du système S peuvent s'obtenir en prenant les formules de la géométrie de la sphère du système  où figure le rayon, et en attribuant à ce rayon la valeur imaginaire k. ; de là l'expression de géométrie imaginaire. Comme on peut au reste éviter l'emploi des imaginaires en substituant aux fonctions trigononométriques ordinaires les fonctions hyperboliques correspondantes, Klein a proposé le terme de géométrie hyperbolique.

Le développement des théories de la géométrie non-euclidienne, continué sans achoppement à aucune contradictien logique, a prouvé d'une façon irréfutable l'impossibilité de démontrer le postulatum d'Euclide et permis de constater que son véritable fondement est l'expérience, celle-ci ne nous permettant aucunement d'attribuer une valeur finie quelconque au paramètre k du système S. Mais il est possible de procéder de même par rapport aux autres postulats de la géométrie euclidienne, en particulier celui qui entre implicitement dans la notion de la ligne droite, en tant qu'elle est conçue comme toujours déterminée par deux de ses points. On suppose en effet que la distance de ces deux points peut croître au delà de toutes limites; si nous admettons au contraire qu'il y a dans l'espace une distance limite maxima, il s'ensuivrait qu'entre deux points séparés par cette distance limite on pourrait mener une infinité de droites, comme sur la sphère on peut mener par deux pôles une infinité de grands cercles. On conçoit dès lors la possibilité de construire une nouvelle théorie différente de celle que nous venons d'exposer et qui lui sera opposée en ce sens que la géométrie euclidienne sera entre les deux la limite commune intermédiaire, correspondant à la valeur infinie du paramètre. Cette seconde géométrie non-euclidienne a été qualifiée de sphérique par Beltrami, d'elliptique par Klein; on la connaît également sous le nom de riemannienne, parce qu'on peut la déduire des principes développés dans un mémoire de Riemann, Sur les Hypothèses qui servent de fondement à la géométrie, mémoire lu en 1854 à la faculté philosophique de Goettingen, mais publié seulement en 1867, comme oeuvre posthume.

Dans ce mémoire, Riemann a envisagé la question au point de vue le plus général possible, en essayant de construire logiquement la notion d'espace. Il conçoit le point mathématique comme un mode de détermination d'une multiplicité continue à trois dimensions mesurables avec une même unité effective, et il remarque que la mesure supposant la superposition des grandeurs à mesurer, nous postulons que la grandeur étalon ne s'altère pas en se déplaçant dans la multiplicité. Dans une variété à une dimension mesurable (où l'on ne passe d'un point à un autre que d'une seule façon déterminée), chaque point P₁ se trouve défini par la valeur numérique de la grandeur qu'il détermine en même temps qu'un autre point O choisi pour origine; cette valeur est sa distance à l'origine ou sa coordonnée x₁. Si cette variété en parcourt une autre à une dimension également mesurable, de sorte que lorsque O sera en un point P₂ de cette seconde variété, le point P₁ soit transporté en un point M, le point M appartient à une multiplicité à deux dimensions, où il sera déterminé par ses coordonnées OP₁, OP₂, soit x₁, x₂. En continuant de la sorte, on engendrera successivement des multiplicités ayant toujours une dimension de plus que la précédente, et dans une multiplicité à n dimensions ainsi construite, un point M est déterminé par les valeurs x₁, x₂..., x_n de ses coordonnées OP₁, OP₂... OP_n, valeurs qui seront les distances à l'origine des points P₁, P₂..., P_n. Mais si les dimensions sont homogènes, on peut, à partir de l'origine, passer au point M en parcourant une variété à une dimension homogène à celles des coordonnées. Le point M a donc, par rapporte l'origine, une distance qui sera d'ailleurs une fonction déterminée des coordonnées. Or, cette fonction est logiquement arbitraire, sous la seule condition d'être toujours positive (sinon nulle) et de devenir égale à une quelconque des coordonnées quand les autres s'annulent. Les espèces du genre de multiplicité défini en dernier lieu sont classées par Riemann d'après la forme des fonctions qui lient aux coordonnées d'un point la distance s de ce point à l'origine. Choisissant l'espèce dans laquelle on a ou on peut avoir, pour un choix convenable des coordonnées, ds² =dx², lorsque l'élément infiniment petit de la distance commence à l'origine, il énonce pour le cas où cet élément commence en un point quelconque, la relation :

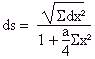En 1868, Beltrami a publié un Essai d'interprétation de la géométrie non-euclidienne, ou ont été démontrées les propositions analytiques énoncées par Riemann. Pour résumer brièvement les résultats de cet essai, je ferai appel à la fiction d'un être intelligent à deux dimensions seulement; sons certaines conditions dans le détail desquelles il est inutile d'entrer ici, on admettra que cet être, s'il vivait sur une surface développable (dont la courbure est nulle) constituerait une géométrie plane identique à la nôtre; la géométrie dans l'espace ne serait d'ailleurs pour lui qu'une conception purement algébrique, comme l'est pour nous celle d'une géométrie à plus de trois dimensions. Si cet être vivait sur une surface à courbure positive constante (sphère ou autre), sa géométrie serait identique à la nôtre pour les figures sphériques; s'il vivait au contraire sur une surface à courbure négative constante (pseudosphérique), sa géométrie serait identique à la planimétrie de Bolyai, s'il dénommait comme droites les lignes géodésiques de la surface. La géométrie non-euclidienne dans le plan reçoit donc une interprétation qu'il faut cependant soumettre à cette restriction, qu'il n'y a pas sur une surface pseudosphérique égalité de courbure dans toutes les directions comme sur la sphère ou le plan, puisque la définition de la courbure négative des surfaces s'oppose nécessairement à cette é alité. Il faut donc, dans l'interprétation de Beltrami, faire abstraction des conséquences de cette variation de la courbure dans différentes directions. On ne peut obtenir, pour la géométrie non-euclidienne dans l'espace, d'interprétation analogue à celle dont est susceptible la planimétrie; mais, de même qu'il a été possible de constituer une théorie en supposant que pat un point on puisse mener plus d'une parallèle à une droite (géométrie de Bolyai), on constituera une théorie dans l'hypothèse que par un point on ne peut mener aucune parallèle à une droite (géométrie de Riemann).

Les travaux postérieurs à ceux de Beltrami, notamment ceux de Klein, ont introduit dans la théorie de nouveaux développements et mis en lumière de nouvelles correspondances analogiques, mais aucun principe important n'est venu s'ajouter à ceux que Riemann a énoncés; les conclusions philosophiques sont dégagées, et s'il peut y avoir intérêt, au point de vue dogmatique, à faire ressortir dans l'enseignement la possibilité logique d'admettre d'autres postulats que ceux de la géométrie euclidienne, nul ne paraît plus songer sérieusement à mettre réellement ces postulats en question au point de vue objectif. A cet égard, la puissance d'abstraction. de la pensée de Riemann a exercé une influence notable; il faut observer, en effet, que Gauss parait avoir réellement douté si l'application des formules euclidiennes au calcul des distances stellaires pourrait donner des résultats rigoureusement exacts; Legendre, tout en essayant de démontrer a priori le postulatum, ne reculait pas devant la discussion a posteriori du problème; Schweikart a inventé le terme de géométrie astrale pour l'appliquer aux théories de Bolyai et de Lobatchevski. 

Après Riemann, la question a changé d'aspect; on se trouve moins en présence d'une question de fait que de celle de la possibilité de se représenter un espace ayant une courbure de grandeur finie, ce qui, malgré tout artifice d'exposition, parait devoir entraîner la considération d'une quatrième dimension géométrique, de mène que la notion de la courbure de surface.suppose une troisième dimension. Or, il est certain que la constitution de nos sens ne nous permet que la représentation objective de trois dimensions, et quo nous ne pouvons dès lors prétendre développer une science applicable à l'espace physique et dépassant notre faculté représentative. Pour nous, la géométrie à n dimensions ne peut être que l'algèbre écrite dans une nouvelle langue conventionnelle. Si nous disons : « trois plans se coupent en général en un point » ou « un système de trois équations du premier degré à trois inconnues admet en général une solution et une seule », nous énonçons, sous deux formes diverses, une mètre proposition logique; comme la première forme est beaucoup plus comte que la deuxième, on a pu espérer simplifier le langage algébrique en le traduisant en un langage géométrique; le nombre des variables en algèbre étant indéterminé, il a fallu aussitôt parler de fi dimensions. Mais, pour cela, on n'a nullement fait de la géométrie, on a continué à faire de l'algèbre. Que dire si on parle d'un espace à m/ n dimensions (Géométrie panimaginiaire, L. Hugo, 1870). (Paul Tannery, ca. 1900).

La géométrie depuis 1900

Après eux, Solomon Lefschetz (1884-1972) contribue à la topologie algébrique, notamment par la théorie des nombres de Lefschetz et l'introduction de nouveaux outils comme les classes caractéristiques. Hassler Whitney (1907-1989), de son côté, travaille sur la théorie des singularités et la topologie des variétés. Marston Morse (1892-1977) développe la théorie qui porte son nom et qui utilise des fonctions différentiables pour étudier la topologie des variétés.

Seconde moitié du XX^e siècle.
Géométrie algébrique moderne.
Alexander Grothendieck (1928-2014) révolutionne la géométrie algébrique avec la théorie des schémas et le concept de topos, qui unifie des aspects de la géométrie et de l'algèbre. Les travaux sur la cohomologie et les faisceaux de Jean-Pierre Serre (né en1926) contribuent à l'unification de la géométrie algébrique et de la topologie.

Théorie des catégories.
Samuel Eilenberg (1913-1998) et Saunders Mac Lane (1909-2005) développent la théorie des catégories, qui devient un outil fondamental en mathématiques, particulièrement en géométrie et en topologie.

Géométrie symplectique et topologie des variétés.
A partir des années 1980, se développent la géométrie symplectique et la topologie des variétés :

Mikhael Gromov (né en1943) iIntroduit des concepts fondamentaux en géométrie symplectique et en géométrie riemannienne, comme la notion de remplissage symplectique et le théorème de non-squeezing.

William Thurston (1946-2012) développe la géométrie des 3-variétés, formulant la conjecture de géométrisation, qui étend les idées de la conjecture de Poincaré. Les travaux sur la topologie des 4-variétés de Simon Donaldson (né en 1957) et les instantons de Yang-Mills ont des implications profondes pour la théorie des variétés.

Premier quart du XXI^e siècle.
Edward Witten (né en 1951) utilise des techniques géométriques pour faire avancer la théorie des cordes. il influence profondément la physique théorique et la géométrie.La symétrie miroir, une coonjecture qui relie la géométrie complexe et la géométrie symplectique, est étudiée par des mathématiciens et des physiciens. Andrew Wiles (né en 1953): résout le dernier théorème de Fermat en utilisant des techniques de géométrie arithmétique et de théorie des nombres.