Les mathématiciens s'étaient à peine assimilé les connaissances qu'ils devaient aux Arabes et aux traductions arabes des auteurs grecs, que les réfugiés, qui s'échappèrent de Constantinople après la chute de l'empire d'Orient, apportèrent en Italie les oeuvres originales et les traditions de la science grecque. Ainsi vers le milieu du XV^e siècle les étudiants d'Europe pouvaient prendre connaissance des principales découvertes des Ecoles grecque et arabe.

L'invention de l'imprimerie à peu près à la même époque rendit relativement facile la diffusion de la science. Il semble inutile de faire remarquer qu'avant l'imprimerie, un écrivain ne pouvait avoir qu'un nombre très limité de lecteurs; mais nous oublions peut-être trop aisément que lorsqu'au Moyen-âge un auteur « publiait » un ouvrage, celui-ci n'arrivait à la connaissance que de bien peu des contemporains de l'auteur. Il n'en avait pas été ainsi dans les temps classiques, car, à cette époque et jusqu'au IV^e siècle de notre ère Alexandrie était regardée comme le centre où convergeaient et d'où partaient tous les nouveaux ouvrages et toutes les découvertes. D'un autre côté, il n'existait au Moyen-âge aucun centre commun où les hommes de science pouvaient se réunir et c'est peut-être à cela qu'il faut attribuer en partie le développement lent et irrégulier des mathématiques médiévales.

L'introduction de l'imprimerie marque le commencement de la vie moderne dans le monde scientifique aussi bien que politique; car elle arrive au moment où l'École européenne (née de la scolastique) s'assimilait les résultats des Ecoles indienne et arabe et des Ecoles grecques).

Pendant la première partie de cette période, l'attention des mathématiciens se concentra principalement sur l'algèbre syncopée et la trigonométrie, mais l'importance relative des mathématiciens de cette période n'est pas très facile à déterminer. Les années qui forment le milieu de la Renaissance se distinguèrent par le développement de l'algèbre syncopée. La fin du XVI^e siècle vit la création,de la dynamique. Vers la même époque et dans les premières années du XVII^e siècle, la géométrie pure attira particulièrement l'attention.

Nous allons rapidement passer en revue la vie et les travaux des hommes qui forment en quelque sorte le foyer du mouvement scientifique moderne. 

Développement de l'algèbre syncopée et de la trigonométrie

Regiomontanus fut un des premiers à tirer parti de la découverte des textes originaux des mathématiciens grecs, pour se familiariser avec leurs méthodes de raisonnement et s'assimiler leurs découvertes; il rapporte avoir vu au Vatican une copie de l'Algèbre de Diophante et c'est la la plus ancienne mention de cet ouvrage, qui ait été faite dans l'Europe moderne. Il connaissait également très bien les oeuvres des mathématiciens arabes.

On peut se rendre compte du bénéfice qu'il a retiré de son étude des mathématiciens anciens d'après son traité De Triangulis omnimodis libri V écrit en 1464 et publié à Nuremberg en 1533. Parfois, il n'y fait que reprendre certains résultats déjà connus des Grecs. On y remarque, entre autres, la proposition suivante : « L'arc du grand cercle qui divise en deux également l'angle au sommet d'un triangle sphérique, fait sur la base deux segments dont les sinus sont entre eux comme les sinus des côtés qui comprennent l'angle ». Mais le grand mérite de l'ouvrage est d'être la plus ancienne exposition moderne systématique de la trigonométrie plane et sphérique ( bien que les seules fonctions trigonométriques qu'on y trouve, ici encore, ne soient que le sinus et le cosinus). L'ouvrage est divisé en cinq livres, les quatre premiers étant consacrés à la trigonométrie plane, et en particulier à la détermination de triangles dépendant de trois conditions données, le cinquième de la trigonométrie sphérique. 

Dans les deux premiers livres, qui renferment beaucoup de problèmes nouveaux, il s'agit toujours de déterminer, au moyen de trois données quelconques, les autres parties d'un triangle. Par exemple, dans la 12^e question du Il^e livre, on donne la base, la perpendiculaire et le rapport des deux côtés. Quand l'auteur dit que cette question n'avait pas encore été résolue par la géométrie, il oubliait qu'elle était déjà connue d'Apollonius (second livre des Lieux plans), de Pappus et d'Eutocius. (La même question avait été traitée par Hassan-ben-Haïthem (dans ses Connues géométriques); elle le fut depuis par Cardan, dans son traité de Proportionibus numerorum; par Galilée, dans les Lieux plans d'Apollonius, restitués par Fermat, etc.; enfin G. Legendre l'a comprise dans son traité de Géométrie élémentaire). Il y applique l'algèbre, ars rei et census, comme il l'appelle d'après Léonard de Pise et qui était alors très fréquemment employée par les astronomes mathématiciens, et arrive ainsi à une équation du second degré.

Comme exemple des problèmes de l'époque, nous reproduisons en entier une de ses propositions. Il s'agit de déterminer un triangle dans lequel on connaît la différence de deux côtés, la perpendiculaire abaissée du sommet commun à ces deux côtés sur la base, et la différence des deux segments déterminés sur la base par le pied de cette perpendiculaire (prop. 23. Livre II).

Voici la solution donnée par Regiomontanus :

Sit talis triangulus ABG, cujus duo latera AB et AG différentia habeant nota HG, ductaque perpendiculari AD duorum casuum BD et DG, différentia sit EG : hae duae differentiae sint datae, et ipsa perpendicularis AD data. Dico quod omnia latera trianguli nota concludentur. Per artem rei et census hoc problema absolvemus. Detur ergo differentia laterum ut 3, differentia casuum 12, et perpendicularis 10. Pono pro basi unam rem, et pro aggregato laterum 4 res, nec proportio basis ad congeriem laterum est ut HG ad GE, scilicet unius ad 4. Erit ergo BD 1/2 rei minus 6, sed AB erit 2 res demptis 3/2. Duco AB in se, producuntur 4 census et 2 1/4 demptis 6 rebus. Item BD in se facit 1/4 census et 36 minus 6 rebus : huic addo quadratum de to qui est 100. Colliguntur 1/4 census et 136 minus 6 rebus aequales videlicet 4 censibus et 2 2/4 demptis 6 rebus. Restaurando itaque defectus et auferendo utrobique aequalia, quemadmodum ars ipsa paececipit, habemus census aliquot aequales numero, unde cognitio rei patebit, et inde tria latera trianguli more suo innotescet :-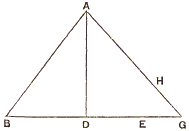

Pour expliquer ce texte nous devons dire que Regiomontanus appelle toujours la quantité inconnue res, et son carré census ou zensus; mais en employant ces termes techniques il écrit les mots en entier. Il commence par dire qu'il va résoudre le problème au moyen d'une équation du second degré (per artem rei et census) ; et qu'il supposera que la différence des côtés du triangle est égale à 3, que la différence des segments de la base est égale à 12, et enfin que la hauteur du triangle est égale à 10. Il prend alors pour inconnue (unam rem ou x) la base du triangle, et par conséquent la somme des côtés sera 4x.

La longueur BD sera alors égale à 1/2 x - 6 (1/2 rei minus 6), et la longueur AB sera égale à 2x - 3/2 (2 res demptis 3/2); par suite  (AB in se) aura pour expression 4x² + 2 1/4 - 6x (4 census et 2 1/4 demptis 6 rebus), et BD² vaudra 1/x² + 36 - 6x. 

A  il ajoute  (quadratum de 10) qui est 100, et fait remarquer que la somme est égale à AB². Cette égalité lui donnera, dit-il, la valeur de x² (census), d'où on peut déduire x (cognitio rei) et le triangle est ainsi déterminé.

Ce raisonnement se traduit comme il suit en langage algébrique moderne :

Nous avons :

Mais d'après les conditions numériques données :

AG - AB = 3 =1/ 4 (DG - DB),

par suite :

AG + AB = 4 (DG + DB) = 4x ;

donc :

AB =2x - 3/2 et BD= 1/2x - 6.

(2x - 3/2)² = (1/2x - 6)² + 100, équation nous donnant x. Tous les éléments du triangle peuvent ensuite être calculés.

Il est bon de faire remarquer que Regiomontanus visait simplement à donner un raisonnement général et les nombres ne sont pas choisis avec l'intention de traiter un problème particulier. Ainsi dans sa figure il ne cherche nullement à prendre la longueur GE égale à quatre fois GH, et comme il trouve en définitive x égal à , le point D tombe en réalité sur le prolongement de la base. Les lettres A, B, G employées pour dénoter le triangle, sont, bien entendu, dérivées de celles de l'alphabet grec qu'il employait.

Quelques unes de ses solutions sont compliquées sans nécessité, mais il ne faut pas oublier qu'à cette époque l'algèbre et la trigonométrie n'étaient pas symboliques, et qu'il est très difficile d'exprimer à chaque instant, en langage ordinaire, ce qu'une formule contient.

On remarquera aussi, d'après l'exemple qui précède, que Regiomontanus n'hésitait pas à appliquer l'algèbre à la solution des problèmes de géométrie. Le recueil, publié par de Murr, sous le titre : Memorabilia Bibliothecarum Norimbergensium et universitatis Altorfinae (Nuremberg, 1786, 2 vol.), contient de Regiomontanus une solution trigonométrique de la fameuse question qui se trouve dans le Siddhanta de Brahmagupta et dont les mathématiciens des XV^e et XVI^e siècles se sont occupés, question qui consiste à à construire un quadrilatère inscrit dans un cercle connaissant les longueurs de ses côtés. Dans sa solution Regiomontanus fait intervenir l'algèbre et la trigonométrie. 

Contemporains de Regiomontanus.
Regiomontanus était un des plus éminents mathématiciens de son époque et nous avons insisté avec quelques détails sur ses ouvrages qui doivent être considérés comme types des productions mathématiques les plus avancées du temps. Quant à ses contemporains, nous nous bornerons presque à citer des noms parmi les plus connus;  ils ne tiennent qu'un rang secondaire et si nous donnons ici une place plus grande à Paciulo, c'est moins pour ses contributions (insignifiantes) aux progrès des mathématiques que pour ce que son oeuvre a de représentatif des mathématiques de son temps. Pour les autres. Il faudra attendre Tartaglia, pour observer de nouveaux progrès.

Le cardinal de Cues.
Nous pouvons mentionner ensuite Nicolas de Cues (1401-1464), dont les écrits mathématiques sont relatifs à la réforme du calendrier et à la quadrature du cercle : dans cette dernière question sa construction revient à prendre  pour la valeur de . Ce même problème suggéra à Nicolas de Cusa l'idée de faire rouler un cercle sur une ligne droite. On a voulu y voir les premières traces de la cycloïde, courbe devenue si célèbre au temps de Pascal. Mais l'arc de cercle ainsi décrit ne servait, dans l'esprit de l'auteur, qu'à déterminer le point de la droite où venait se placer, après une révolution du cercle, le point de sa circonférence qui touchait d'abord cette droite, et qu'il ne s'agissait nullement de considérer la courbe engendrée dans l'espace pour un point de la circonférence qu'on faisait mouvoir sur une ligne droite.

Purbach.
Georg von Purbach (1423-1461), qui avait été l'élève de Nicolas de Cues et fut, comme on l'a dit, le maître de Régiomontanus, est l'auteur d'ouvrages d'astronomie (Theoricae novae planetarum), d'une arithmétique (Elementa Arithmetices Algorithmus de numeris integris) publiée en 1511 et d'une table des sinus naturels (Tractatus Georgii Purbachii super Propositiones Ptolemaei de sinubus et chordis) publiée en 1541.

Chuquet.
Citons également ici un traité sur l'arithmétique, intitulé LeTriparty écrit en 1484 par Nicolas Chuquet (ca. 1445-1488), qui était un bachelier en médecine de l'Université de Paris. Cet ouvrage, écrit en français, montre que le programme des mathématiques enseignées à cette époque était un peu plus développé qu'on l'a cru longtemps. On y trouve l'usage le plus ancien du signe radical avec, indices pour indiquer l'extraction de racines, l'indice 2 pour la racine carrée, l'indice 3 pour la racine cubique, et ainsi de suite, il contient également une exposition nette de la règle des signes. Les mots plus et moins sont indiqués par les contractions . (L'introduction des principaux symboles de l'algèbre).

Léonard de Vinci.
La réputation de Léonard de Vinci (1452-1519) comme artiste a éclipsé ses titres à la renommée comme mathématicien, mais on peut dire qu'il a préparé la voie à une conception plus juste de la mécanique et de la physique, et par sa réputation et son influence, il attira un peu l'attention sur ce sujet; il fut un ami intime de Paciuolo. L'oeuvre mathématique de Vinci est incomplète, et consiste surtout en idées émises sans discussion détaillée et qu'il ne pouvait pas vérifier, ou, dans tous les cas, qu'il n'a pas vérifiées. Ses écrits mathématiques se rapportent principalement à la mécanique, à l'hydraulique et à l'optique; ses conclusions sont généralement basées sur des expériences. L'exposition qu'il donne de l'hydraulique et de l'optique contient fort peu de mathématiques. La mécanique renferme de nombreuses et de sérieuses erreurs; les parties les mieux traitées sont celles relatives à l'équilibre d'un levier soumis à l'action de forces quelconques, aux lois du frottement, à la stabilité d'un corps suivant la position de son centre de gravité, à la résistance des poutres, et à l'orbite décrite par un point sous l'action d'une force centrale; il traita également quelques problèmes faciles au moyen des moments virtuels. On lui attribue parfois la connaissance du triangle des forces, mais il est probable que ses idées sur cette question n'étaient pas très nettes. 

Si l'on croit  Lomazzo (Tratatto della Pittura), Vinci fut l'inventeur du tour à ovale. Le tour à ovale reposait sur une idée tout à fait nouvelle pour tracer les courbes. On ne les avait jusqu'alors décrites que par la trace d'un style mobile, imprimée sur un plan fixe. L. de Vinci y procéda inversement, au moyen d'un stylet fixe, imprimant sa trace sur un plan mobile. Tel est le tour à ovale, qui sert à tracer l'ellipse. Quel mouvement fallait-il donner au plan mobile, pour obtenir ainsi une ellipse? Le peintre a su découvrir, parmi une infinité de solutions dont cette question était susceptible, sans doute la plus simple, celle qui consiste à donner au plan mobile le mouvement d'un angle de grandeur constante, dont les deux côtés glissent sur deux points fixes. Cette question, si intéressante, de la génération de l'ellipse, n'a été traitée depuis que par Clairaut (en 1740).

Dürer.
Albert Dürer (1471-1528) appartient, comme Léonard de Vinci, à cette génération de grands artistes, peintres, sculpteurs et architectes, pour lesquels la géométrie est non seulement un instrument d'analyse, mais un puissant moyen de perfectionnement. 'étude de la perspective le conduisit à la transformation des figures en d'autres figures du même genre. Et de là naquirent plusieurs méthodes géométriques, comme celle qui consiste à faire croître proportionnellement les ordonnées des points d'une figure, dans le dessin d'un profil dont on veut rendre les dimensions en hauteur plus facilement appréciables. Dürer maniait très habilement le compas pour tracer des ellipses et d'autres figures géométriques. Le pentagone de Dürer est un pentagone régulier, construit avec une seule ouverture de compas; mais d'autres géomètres (Clavius, J. B. Benedetti) ont démontré depuis que ce pentagone n'a pas tous les angles égaux et que sa figure n'est qu'approximative. Les Instructions de Dürer concernant l'usage du compas parurent en allemand, à Nuremberg, 1525, avec 19 figures sur bois, probablement gravées par Dürer lui-même. On en publia des traductions latines en 1532, 1555 et 1605. 

Paciulo.
Luca Paciuolo (ca. 1445 - ca. 1514) enseigna les mathématiques à Rome, Pise, Venise et Milan; dans cette dernière cité il occupa le premier une chaire de mathématiques fondée par Sforza.

Son principal ouvrage fut imprimé à Venise en 1494 et est intitulé Summa de arithmetica, geometria, proporzioni e proporzionalita. C'est le plus ancien livre d'arithmétique et d'algèbre qui ait été imprimé. Il est basé principalement sur les écrits de Léonard de Pise (Fibonacci), et son importance dans l'histoire des mathématiques est en grande partie due à ce fait, qu'il fut beaucoup répandu. Il comprend deux parties-: la première traite de l'arithmétique et de l'algèbre, la seconde de la géométrie. 

En arithmétique Paciuolo donne des règles pour les quatre opérations élémentaires et une méthode pour l'extraction des racines carrées. Il traite fort bien toutes les questions relatives à l'arithmétique commerciale en donnant de nombreux exemples, et en particulier s'occupe avec beaucoup de détails des lettres de change et de la théorie de la tenue des livres en partie double. Cette partie constitue la première exposition systématique d'une arithmétique algorithmique. Cet ouvrage et l'ouvrage semblable de Tartaglia constituent les deux autorités classiques sur le sujet. La plupart des problèmes sont résolus par la méthode de fausse supposition, mais on y rencontre. plusieurs erreurs numériques.

L'exemple suivant nous donnera une idée du genre de problèmes d'arithmétique discutés.

J'achète pour 1440 ducats à Venise 2400 pains de sucre, dont le poids net est 7200 livres; je paye pour le salaire de l'agent 2% ; aux peseurs et aux chargeurs en tout 2 ducats; après cela je dépense en achat de caisses, cordes, toile et pour le salaire des emballeurs une somme de 8 ducats; pour la taxe ou droit d'octroi sur le premier montant de mon achat, 1 ducat pour cent; après cela pour droit et taxe au bureau des exportations, 3 ducats pour cent; pour inscription des adresses sur les caisses et enregistrements de leur passage 1 ducat; pour le trois-mâts barque jusqu'à Rimini, 13 ducats; en cadeaux au capitaine et en pourboire pour l'équipage en différentes occasions, 2 ducats;. en achat de provisions pour moi et un domestique durant un mois. 6 ducats; en dépenses occasionnées par plusieurs petits voyages par voie  de terre faits çà et là, pour les barbiers, le lavage du linge, et en bottes pour moi et mon domestique, 1 ducat; à mon arrivée à Rimini je paye au capitaine du port pour droit de port en monnaie de la cité, 3 lires; aux porteurs, pour le débarquement sur terre, et le transport en magasin, 5 lires; comme taxe d'entrée 4 soldi la charge, qui est représentée en nombre par 32 (suivant la coutume); pour un baraquement à la foire 4 soldi par charge; plus tard je trouve que les mesures employées à la foire diffèrent de celles usitées à Venise, et qu'un poids de 140 lires là est équivalent au poids de 100 lires à Venise; de plus 4 lires de leur monnaie d'argent équivalent à 1 ducat or. Je demande par suite combien il me faut vendre cent lires Rimini afin de réaliser un gain de 10% sur mon marché, et qu'elle est la somme que je recevrai en monnaie vénitienne?

« Si res et census numero coaequantur, a rebus 
dimidio sumpto censum producere debes, 
addereque numero, cujus a radice totiens
tolle semis rerum, census latusque redibit. »

Bien que beaucoup des matières dont nous venons de parler soient empruntées au Liber Abaci de Fibonacci, cependant la notation dont il se sert est supérieure à celle de ce dernier. Paciuolo imite Fibonacci et les Arabes en appelant la quantité inconnue la chose, en italien cosa - ce qui fait que l'algèbre a été quelquefois appelée l'art de la chose - ou en latin res, et il la dénote quelquefois par co ou R ou Rj. Il appelle le carré de la quantité inconnue census ou zensus et le désigne parfois par ce ou Z; de même le cube de la quantité inconnue ou cuba, est représenté par cu ou C; la quatrième puissance, ou censo di censo s'écrit tout au long comme nous venons de le faire ou ce di ce ou encore ce ce. Il est à noter que toutes ses équations sont numériques, c'est-à-dire qu'il n'eut pas l'idée de représenter les quantités connues par des lettres comme l'avait fait Jordanus Nemorarius et comme cela se pratique en algèbre moderne; mais Libri cite deux exemples, dans lesquelles il représente dans une proportion un nombre par une lettre. Il indique l'addition et l'égalité par les lettres initiales des mots plus et aequalis, mais il évite généralement l'introduction d'un symbole pour moins en écrivant ses quantités dans le membre de l'équation où elles seront prises positivement, bien que dans quelques endroits il emploie  pour moins ou de pour demptus. C'est là un commencement d'algèbre syncopée.

On ne trouve rien de frappant dans les résultats auxquels il arrive dans la seconde partie de son ouvrage, c'est-à-dire la partie géométrique, pas plus que dans deux autres traités de géométrie, qu'il écrivit et qui furent imprimés à Venise en 1508 et 1509. Il faut remarquer cependant que, de même que Regiomontanus, il fit intervenir l'algèbre pour s'aider dans la recherche des propriétés géométriques des figures.

Le problème suivant donnera un exemple du genre de questions géométriques qu'il traitait.

Sachant que le rayon du cercle inscrit dans un triangle vaut 4 unités de longeur et que les segments déterminés sur l'un des côtés par le point de contact correspondant ont respectivement pour longueurs 6 unités et 8 unités, calculer les autres côtés.

Pour résoudre la question il suffit de remarquer que , ce qui donne , d'où p = 21 ; par conséquent les côtés cherchés sont 21 - 6 et 21 - 8, c'est-à-dire 15 et 13.

Mais Paciuolo ne fait pas usage de cette formule (qu'il connaissait); il donne une laborieuse construction géométrique, puis fait intervenir l'algèbre pour trouver les longueurs des divers segments des lignes dont il a besoin. Son exposé nous semble trop long pour être reproduit ici, mais l'analyse suivante est suffisamment complète pour permettre de le reconstituer.

Soit ABC le triangle et D, E, F les points de contact des côtés avec le cercle inscrit de centre O. Soient H le point d'intersection de OB et DF, K le point d'intersection de OC et DE. Désignons par L et M les pieds des perpendiculaires abaissées de E et F sur BC. Traçons EP parallèle à AB et coupant BC en P. Alors Paciuolo détermine successivement les grandeurs des lignes suivantes : 1°, OB ; 2°, OC ; 3°, FD ; 4°, FH ; 5° ED ; 6°, EK. Puis il forme une équation du second degré dont les racines lui fournissent les valeurs de MB et MD. Il obtient d'une façon semblable les valeurs de LC et LD. Il calcule ensuite successivement les valeurs de EL, FM, EP et LP et par les triangles semblables obtient la valeur de AB qui est égale à 13.

Cette démonstration fut, même soixante ans plus tard, citée par Cardan comme «-incomparablement simple et parfaite, et la vraie couronne des mathématiques ».

Nous en avons fait mention pour donner un exemple des méthodes embarrassées et peu élégantes alors courantes. Les problèmes énoncés sont tout à fait semblables à ceux du De Triangulis de Regiomontanus.

Copernic.
L' hypothèse de Nicolas Copernic (1473-1543) sur le mouvement de la Terre et des planètes autour du Soleil appartient à l'astronomie plutôt qu'aux mathématiques. Cependant nous pouvons mentionner ici  son de Lateribus et angulis triangulorum, etc., libellus (Wittemberg, 1542), petit traité de trigonométrie, où l'auteur démontre, avec clarté mais sans y ajouter rien de neuf, divers théorèmes de Ptolémée et reprend en sous-oeuvre le travail de Regiomontanus. Copernic n'a fait aucun usage des tangentes, qu'il ne paraissait même pas avoir connues.

Il est évident d'après cette publication et d'après son astronomie qu'il était bien au courant de la littérature mathématique, et qu'il en avait la parfaite intelligence. Nous avons mentionné son hypothèse sur le mouvement de la terre comme une simple conjecture de sa part il l'a en effet émise pour expliquer, d'une façon simple, les phénomènes naturels. Galilée en  1632 fut le premier qui essaya de donner un commencement de preuve à l'appui de cette hypothèse.

Recorde.
Le signe employé actuellement pour indiquer l'égalité fut introduit par Robert Recorde (1510-1558). En 1540 il publia une arithmétique, intitulée le Grounde of Artes (le Jardin des Arts), dans laquelle il emploie le signe + pour indiquer l'excès et le signe - pour indiquer le déficit ;

« + whyche betokeneth too wuch, as this line - plaine without a crosse line, betokeneth too little. »  (+ qui indique trop, comme cette ligne - tracée sans un trait transversal indique trop peu).

Il écrivit aussi une astronomie. Ces ouvrages, comme ceux de Paciuolo, donnent une idée nette des connaissances du temps.

Riese. Rudolff
Vers la même époque en Allemagne, Riese et Rudolff reprirent la question de l'arithmétique et de l'algèbre. Leurs recherches servirent de base à l'ouvrage bien connu de Stifel. 

Adam Riese (né en 1489 près de Bamberg, mort en 1559) a composé, en vieux dialecte allemand, un Traité de calcul linéaire (Erfurt, 1522) , un un traité de géométrie pratique, mais son ouvrage le plus important est un Traité d'arithmétique (Leipzig, 1536, 1539) , qui est en même temps une algèbre. Dans cet ouvrage, basé sur le livre de Paciuolo. Riese employait les symboles + et -.

Christoff Rudolff(1499-1545) publia son algèbre en 1525; elle est intitulée Die Coss, ou, selon la traduction latine conservée dans les manuscrits de la Bibliothèque nationale (n° 7365, in-4), Arithmetica Christophori Rodolphi ab Jamer, e germanica lingua in latinam a Christ. Auvero.... Romae anno Christi 1540 conversa. On y trouve des progrès sensibles de l'algèbre et de ses applications à la géométrie. Rudolff s'y s'appuie, lui aussi, sur les écrits de Paciuolo et peut-être de Jordanus Nemorarius. Il introduisit le signe  pour indiquer la racine carrée, ce symbole étant une corruption de la lettre initiale du mot radix (racine), de même  indiquait la racine cubique, et  la racine quatrième.

Les méthodes usitées par Rudolff et Riese et leurs découvertes furent rassemblées et exposées d'une façon générale dans un ouvrage de Stifel qui se répandit au loin.

Stifel.
Michael Stifel (ca. 1486-1567), connu quelquefois sous le nom latin de Stiffelius était un ami personnel de Luther. Il écrivit un petit traité sur l'algèbre, mais son principal, ouvrage mathématique est son Arithmetica Integra publiée à Nuremberg en 1544, avec une préface de Melanchthon.

Dans les deux premiers livres de son Arithmetica Integra il traite des radicaux et des incommensurables en adoptant la forme euclidienne. Le troisième livre relatif à l'algèbre, est à remarquer car il a appelé l'attention générale sur la pratique alors adoptée en Allemagne où l'on se servait des signes + et - pour indiquer l'addition et la soustraction. On relève quelques faibles indices montrant que ces signes ont été employés occasionnellement par Stifel comme symboles d'opération et non uniquement comme abréviations; cette application était probablement nouvelle. Non seulement il employait. les abréviations usuelles pour les mots italiens représentant la quantité inconnue et ses puissances; mais dans un cas au moins, lorsqu'il se trouvait en présence de plusieurs quantités inconnues, il les représentait respectivement par les lettres A, B, C, ... etc. Il réintroduisait ainsi la notation algébrique générale tombée en désuétude depuis le temps de Jordanus Nemorarius.

On a parfois dit que Stifel fut le réel inventeur des logarithmes, mais il est aujourd'hui certain que cette assertion repose sur une fausse interprétation d'un passage dans lequel  il compare les progressions géométriques et arithmétiques. On a dit encore que Stifel avait indiqué une formule permettant d'écrire les coefficients des divers termes du développement de (I + x)ⁿ connaissant ceux du développement de (I + x)^n-1.
-

Deux pages avec figures de l'Arithmetica integra, de Stifel.

En 1553 Stifel fit paraître une édition de l'ouvrage de Rudolff, Die Coss, dans lequel il introduisait un perfectionnement dans la notation algébrique de l'époque. Les symboles ordinairement employés alors pour désigner la quantité inconnue et ses puissances étaient des lettres qui représentaient les mots abrégés. Parmi les plus usitées se trouvaient R ou Rj pour racine ou res (x), Z ou C pour zensus ou census (x²). C ou K pour cubus (x³) etc. Ainsi x² + 5x - 4 s'écrivait ainsi IZp. 5Rm. 4; p et m signifiant plus et moins. On employait également d'autres lettres et d'autres symboles : ainsi Xylander (1575) aurait écrit la même expression comme il suit : IQ + 5N-4.

Viète et même Fermat emploieront quelquefois une notation semblable à cette dernière. La modification faite par Stifel consistait à introduire les symboles IA, IAA, IAAA, pour la quantité inconnue, son carré et son cube; on voyait ainsi immédiatement et d'un coup d'oeil les liaisons qui existaient entre eux.

Tartaglia. 
Niccolo Fontana généralement connu sous le nom de Tartaglia (1500-1557). Il débuta dans la vie publique en professant à Vérone, mais un peu avant 1535, il fut désigné pour occuper une chaire de mathématiques,à Venise. Il y vivait quand il accepta un défi d'un certain Antoine del Fiore (ou Florido), ce qui contribua à le rendre fameux.

Fiore avait appris de son maître, Scipione del Ferro (1465-1526), professeur de mathématiques  à Bologne, une solution empirique des équations du troisième degré de la forme x³ + qx = r. Cette solution était antérieurement inconnue en Europe et il est possible qu'elle avait été trouvée par Ferro dans un ouvrage arabe. Tartaglia, en réponse à une requête de Colla en 1530, avait avancé qu'il pouvait effectuer la solution d'une équation numérique de la forme x³ + px² = r.

Fiore, pensant que Tartaglia était un imposteur, lui envoya un défi, dont les conditions étaient les suivantes : chacun des compétiteurs devait déposer un certain enjeu entre les mains d'un notaire et celui qui donnerait la solution du plus grand nombre de problèmes, dans une série de trente questions proposées par l'autre, entrerait en possession des enjeux; un délai de trente jours était d'ailleurs accordé à chacun d'eux pour résoudre les questions. Tartaglia savait que son adversaire connaissait la solution d'une équation cubique d'une certaine forme particulière, et, supposant que les questions qui lui seraient proposées dépendraient toutes de la solution d'équations de ce genre, se proposa le problème, d'en trouver une solution générale, et parvint certainement à la solution de quelques unes sinon de toutes. On pense que sa solution reposait sur une construction géométrique, et conduisait à la formule qui est souvent, bien qu'à tort, attribuée à Cardan.

Le moment du concours arrivé, toutes les questions proposées à Tartaglia dépendaient, comme il l'avait deviné, de la solution d'une équation cubique, et il parvint dans l'espace de deux heures à les ramener à des cas particuliers de l'équation x³ + qx = r, dont il connaissait la solution. Son compétiteur échoua dans la solution de tous les problèmes qui lui étaient proposés et qui, cela va sans dire, se ramenaient tous à des équations numériques de la forme x³ + px² = r. Tartaglia fut par conséquent proclamé le vainqueur et il composa quelques vers en l'honneur de sa victoire.

Les principaux ouvrages de Tartaglia sont les suivants :

1° Sa Nova Scienza publiée en 1537 : dans ce livre il étudie la chute des corps sous l'influence de la gravité; et il détermine la portée d'un projectile, en constatant qu'elle est maximum quand l'angle de projection est de 45°, mais ce résultat semble avoir été la conséquence d'une heureuse conjecture.
Frontispice du Nova Scienza de Tartaglia.

2° Ses Inventioni, ouvrage publié en 1546 et contenant entre autres sa solution des équations cubiques.

3° Son Trattato de numeri e misuri, consistant en une arithmétique, publiée en 1556, et en un traité sur les nombres, paru en 1560; il montre dans cet ouvrage comment les coefficients de x dans le développement de (I + x)ⁿ peuvent se déduire, en faisant usage d'un triangle arithmétique, de ceux du développement de (r + x)^n-1 pour les cas où l'on fait n successivement égal à 2, 3, 4, 5, ou 6.

Le traité sur l'arithmétique et les nombres est un de ceux qui font principalement autorité pour nous renseigner sur l'ancien algorithme italien. Il est prolixe, niais il nous fait une claire exposition des différentes méthodes arithmétiques alors en usage; il renferme de nombreuses notes historiques qui, autant que nous pouvons les vérifier, sont dignes de confiance. Il contient un nombre considérable de problèmes sur toutes espèces de questions pouvant se présenter en arithmétique commerciale, et on y trouve plusieurs tentatives pour établir des formules algébriques s'appliquant à des problèmes particuliers.

Ces problèmes donnent incidemment nombre de bonnes informations sur la vie ordinaire et les coutumes commerciales du temps. Nous trouvons ainsi que l'intérêt de l'argent pour les placements offrant toute sécurité variait de 5 è 12% l'an; tandis que l'intérêt pour les transactions commerciales était de 20% l'an et plus. Tartaglia montrait le côté défectueux de la loi défendant l'usure, en expliquant comment elle était tournée dans les questions de fermage. Les fermiers endettés étaient mis par leurs créanciers dans l'obligation de vendre toutes leurs récoltes immédiatement après la moisson; le marché se trouvant ainsi encombré, les prix de vente étaient très faibles, et les prêteurs d'argent achetaient à marché ouvert à des conditions extrêmement avantageuses. Les fermiers devaient alors emprunter le grain pour les semailles, à la condition de le remplacer par une quantité égale ou d'en payer le prix dans le courant du mois de mai, quand le cours du blé était le plus élevé. De même Tartaglia, à qui les magistats de Vérone avaient demandé d'établir une échelle mobile permettant de fixer le prix du pain d'après lè cours du blé, entre dans une discussion sur les principes qu'on appliquait à son époque pour régler cette question. Dans un autre endroit il donne les règles usitées pour la préparation des médicaments.

Paciuolo avait donné dans son arithmétique quelques problèmes plaisants, et Tartaglia l'imita en insérant une large collection de récréations mathématiques. Il s'en excuse à moitié en disant qu'il n'était pas rare à la fin du repas de proposer à la compagnie et comme sujet d'amusement des questions d'arithmétique, c'est pourquoi il ajoute quelques problèmes agréables. Il donne plusieurs questions relatives à la manière de deviner un nombre pensé par un membre de la compagnie, sur les liens de parenté créés par les mariages entre parents, ou sur les difficultés provenant de legs contradictoires.

D'autres récréations sont du genre de celles qui suivent :

« trois jolies dames ont pour maris des hommes jeunes, agréables et galants, mais jaloux. Voyageant de compagnie, ils trouvent sur les bords d'une rivière qu'il faut traverser un petit bateau ne pouvait contenir que deux personnes à la fois. On demande comment s'effectuera le passage étant entendu que, pour éviter tout scandale, aucune femme ne sera laissée dans la société d'un homme, à moins que son mari ne soit présent?  »

« Un vaisseau portant comme passagers 15 Turcs et 15 chrétiens, est saisi par la tempête, et le pilote déclare que le salut du bâtiment et de l'équipage exige que la moitié des passagers soit précipitée dans la mer. Pour faire le choix de ceux qui vont être sacrifiés, les passagers sont disposés en rond et il est convenu qu'en commençant à compter à partir d'un point déterminé, chaque neuvième homme sera jeté par-dessus bord. De quelle façon doit-on les disposer pour que les Turcs soient seuls désignés par le sort?-»

« Trois hommes dérobent un vase contenant z24 onces de baume. En fuyant ils rencontrent dans un bois un marchand auquel ils achètent hâtivement trois vases. Arrivés dans un endroit sûr, ils se proposent de partager leur butin, mais ils constatent alors que leurs vases ne contiennent respectivement que 5, 11 et 13 onces. On demande comment-ils vont s'y prendre pour faire trois part égales ? »

Cardan.
Girolamo Cardano (Jerôme Cardan) (1501-1576), après avoir pris ses grades à l'université de Padoue, commença par exercer la médecine à Sacco et Milan de 1524 à 1550; ce fut pendant ce temps qu'il étudia les mathématiques et publia ses principaux ouvrages, dont le plus important est l'Ars Magna, publié à Nuremberg en 1545. Cardan s'intéressait beaucoup à la lutte engagée entre Tartaglia et Fiore, et, comme il avait déjà commencé à écrire son livre, il demanda à Tartaglia de lui communiquer sa méthode de résolution de l'équation cubique. Tartaglia refusa, sur quoi Cardan l'injuria dans les termes les plus violents, mais peu après il lui écrivit en lui disant qu'un certain noble Italien, ayant entendu parler de sa réputation, était très désireux de faire sa connaissance, et il l'engageait à venir de suite à Milan. Tartaglia s'y rendit, et, bien que n'ayant trouvé aucun gentilhomme qui l'attendit, il céda néanmoins aux instances de Cardan et lui donna la règle tant désirée; Cardan de son côté prit l'engagement par serment de ne jamais la révéler et même de ne pas la confier au papier excepté en caractères chiffrés. La règle est énoncée en quelques vers irréguliers qui existent encore. Cardan affirme qu'on ne lui communiqua que le résultat, et que la démonstration est de lui, mais le fait est douteux. Il semble avoir aussitôt enseigné la méthode, et l'un de ses élèves, Ferrari, ramena l'équation du quatrième degré à une équation cubique et la résolut ainsi.

Quand l'Ars Magna fut publié en 1545, sa mauvaise foi devint manifeste. Tartaglia en éprouva naturellement une profonde irritation, et, après une controverse acrimonieuse, il envoya à Cardan un cartel le provoquant pour une lutte mathématique. Les préliminaires furent arrêtées et le lieu de la réunion devait être une certaine Eglise de Milan, mais le jour fixé arrivé, Cardan fit défaut et envoya Ferrari à sa place. Des deux côtés on se déclara vainqueur, bien que nous pensions que c'est Tartaglia qui réussit le mieux dans les épreuves imposées; dans tous les cas la dissolution de la réunion fut provoquée par son compétiteur et il dut s'estimer heureux de pouvoir s'enfuir avant d'être assommé. Non seulement la fraude profita à Cardan, mais les écrivains modernes lui ont souvent attribué la solution en question, de telle sorte que Tartaglia n'eut même pas la réparation posthume qui lui était au moins due.

L'Ars Magna est un ouvrage bien plus avancé qu'aucune des algèbres publiées antérieurement. Jusqu'à ce moment les algébristes s'étaient bornés à fixer leur attention sur les racines positives des équations. Cardan discuta les racines négatives et même imaginaires, et prouva que les dernières se présentaient toujours par couple, mais il se refusa à chercher une explication quant à la signification à attribuer à ces quantités « sophistiques » qui, disait-il, étaient ingénieuses bien qu'inutiles. Une grande partie de son analyse des équations cubiques semble être originale; il montra que si les trois racines sont réelles, la solution de Tartaglia les donne sous une forme qui, contenant des quantités imaginaires, ne permet pas de les calculer. A l'exception de recherches, à peu près semblables à celles que publia Bombelli quelques années plus tard, la théorie des quantités imaginaires attira peu l'attention des mathématiciens postérieurs, jusqu'à ce qu'Euler et Jean Bernoulli eussent repris cette question après un intervalle d'environ deux siècles. Gauss le premier posa les bases méthodiques et scientifiques du sujet, introduisit la notation des variables complexes, et employa le symbole i, qui avait été introduit par Euler, pour dénoter la racine carrée de -1; la théorie moderne est en grande partie basée sur ses recherches.

Cardan établit les relations entre les coefficients et les racines d'une équation. Il avait également connaissance du principe sur lequel repose « la règle des signes » de Descartes, mais, suivant la coutume alors en usage, il écrivait ses équations comme l'égalité de deux expressions, dans chacune desquelles tous les termes étaient positifs, de sorte qu'il ne lui était pas possible d'exprimer la règle d'une façon concise. Il donna une méthode pour déterminer une racine approchée d'une équation numérique, basée sur ce fait que, si une fonction change de signe quand on remplace la variable par deux nombres différents, l'équation obtenue en égalant la fonction à zéro aura une racine comprise entre ces deux nombres.

La solution de l'équation du second degré de Cardan est géométrique et en substance la même que celle donnée par al-Khwarismi. Sa solution d'une équation cubique est également géométrique, et se comprendra d'après l'exemple suivant qu'il donne dans le chapitre XI de l'Ars Magna.

Pour résoudre l'équation x³ + 6x = 20 (ou toute autre équation de la forme x³ + qx = r), on prend deux cubes tels que le produit de leurs arêtes soit 2 (ou 1/3q) et ayant pour différence de leurs volumes 20 (ou r). Alors x sera égal à la différence entre les arêtes des cubes. Pour vérifier cette règle, il pose d'abord ce lemme géométrique : 

Si on enlève d'une ligne AC une certaine portion CB, la différence entre les cubes construits sur AC et BC surpassera le cube construit sur AB de trois fois le parallélépipède droit ayant respectivement pour arêtes AC, BC et AB.

De même que les mathématiciens précédents, il donne des démonstrations séparées de sa règle pour les différentes formes que l'équation est susceptible de prendre. Ainsi il établit une formule de résolution différente pour les équations de chacune des formes-:

x³ + px = q
x³ = px + q
x³ + px +q = 0
x³ + q = px

 « On lui doit aussi une méthode pour les résolutions approchées des équations, fondée sur le changement du signe qui s'opère lorsqu'on substitue successivement, à la place de l'inconnue, deux membres entre lesquels est comprise une racine. Il a trouvé plusieurs des relations qui lient les racines aux coefficients des équations. Il a connu et traité les racines inégales; il s'est même approché du théorème de Descartes, sur les variations et les successions du signe; et l'on voit que s'il n'avait pas été arrêté par la méthode des Arabes, suivie encore au XVI^e siècle, de ne pas égaler l'équation à zéro, mais de la partager en deux membres composés de termes tous positifs, il aurait certainement découvert la plupart des théorèmes qui constituent la théorie générale des équations. Bien qu'il n'ait pas démontré d'une façon générale la réalité des trois racines de l'équation du troisième degré, dans le cas où elles se présentent toutes sous la forme imaginaire, cependant Cardan a prouvé leur réalité dans un grand nombre de cas, surtout en les déterminant géométriquement par les sections coniques. Les Arabes avaient déjà fait des recherches analogues; mais Cardan ignorait leurs travaux, et sa construction de l'équation du troisième degré mérite d'être remarquée, car elle renferme la première idée de la représentation générale du rapport qui existe entre deux quantités par les rapports qui lient les abscisses et les ordonnées dans une courbe quelconque. » (Guglielmo Libri, Histoire des sciences mathématiques en Italie, 1838).

Ferrari. 
Lodovico Ferraro, généralement appelé Ferrari  (1522-1562), et dont nous avons déjà cité le nom ci-dessus au sujet de la solution de l'équation biquadratique, avait été pris par Cardan à son service. Tous les travaux de Ferrari se trouvent dans l'Ars Magna de Cardan ou dans l'Algèbre de Bombelli, mais on ne peut rien lui attribuer d'une façon certaine à l'exception de la solution de l'équation biquadratique. Colla avait proposé comme un défi aux mathématiciens la solution de l'équation : x⁴ +6x² + 36 = 60x, équation particulière, probablement trouvée dans quelque livre arabe. On ne connaît rien au sujet de l'histoire de ce problème, si ce n'est que Ferrari réussit là où Tartaglia et Cardan avaient échoué.

Rhéticus.
George Joachim Von Lauchen, dit Rheticus (1514-1576) était professeur à Wiittenberg. Il étudia par la suite sous la direction de Copernic, qui lui laissa le soin de publier ses ouvrages. Rhéticus construisit diverses tables trigonométriques qui  furent par la suite complétées et étendues par Viète et Pitiscus et servirent ainsi de fondements à celles encore en usage. Rhéticus trouva également les valeurs de sin 2 et sin 3 en fonction de sin et cos et il n'ignorait pas que les rapports trigonométriques peuvent se définir au moyen des rapports des côtés d'un triangle rectangle sans faire intervenir le cercle. Il fit, le premier, usage des sécantes. 

Son principal ouvrage, publié sur ce sujet, a pour titre Canon doctrinae triangulorum (Nuremberg, 1551, et Bâle, 1580) ; c'était l'ébauche d'un grand travail dans lequel l'auteur calcula les sinus, cosinus, tangentes, cotangentes, de dix en dix secondes, pour un rayon de 10 000 000 000. Le manuscrit en avait été légué à un disciple de Rhétieus, à Valentin Otto, qui le fit paraître, en 1596, à Heidelberg, sous le titre de Opus Palatinum de triangulis. Cet ouvrage contient : Libri tres de fabrica canonis doctrinae triangulorum; - de Triquetris rectarum linearum in planitie; - de Triangulis globi cum angulo recto; Magnus canon triangulorum.

Dans une lettre écrite à Ramus en 1568, Rhéticus annonçait l'intention de publier divers ouvrages, entre autres sur l'astronomie et la chimie, où l'observation devait remplacer toutes les vaines théories. Malheureusement aucun de ces ouvrages n'a vu le jour.

Nous ajoutons ici les noms de quelques autres mathématiciens célèbres qui vivaient à peu près à la même époque, bien que leurs ouvrages aient actuellement moins d'intérêt.

Patrizzi.
Francesco Patrizzi  (1529,-1597) essaya le premier d'introduire la métaphysique dans la géométrie, et voulut démontrer les axiomes dans son traité Della nuova geometria; 1587.

Nuñez.
Pedro Nuñez (1492-1577), plus connu sous le nom latinisé de Nonius, donna, dans son remarquable opuscule de Crepusculis (Lisbonne, 1542), la solution d'un problème (trouver le jour de l'année où le crépuscule est le plus court) que Jacques Bernoulli avouera avoir cherché longtemps vainement à résoudre. Dans son traité de Arte atque ratione navigandi libri duo, Coïmbra, 1546, on trouve les premiers indices de la théorie des loxodromies. Frappé par les défauts des cartes plates, dont les navigateurs faisaient alors usage, il chercha à les rectifier; et, dans ce but, il examina les lignes, nommées loxodromiques, qui figurent les rumbs du vent partant de l'équateur, la longueur du chemin parcouru et le changement de longitude, en supposant un changement de latitude de dix minutes en dix minutes.

Maurolico.
Francesco Maurolico, plus connu sous le nom latinisé de Maurolycus, est  né à Messine le 16 septembre 1494, mort le 21 juillet 1575, était d'une famille grecque, originaire de Constantinople.  Précepteur du fils aîné du vice-roi Jean de Vega, il séjourna quelque temps à Palerme, où il se lia d'amitié avec Jean Ventimiglio, marquis de Gerace, qui l'emmena à Naples et à Rome. De retour à Messine, il y enseigna les mathématiques, jusqu'à l'époque de sa mort. Outre un grand nombre de traductions latines de mathématiciens grecs (Archimède, Euclide, Apollonius, Théodose, Ménélaüs), on lui doit plusieurs travaux originaux sur la cosmographie, l'optique, la mécanique et la gnomonique, consignés dans ses Opuscula mathematica (Venise, 1575). Il remarqua, entre autres, que l'ombre de l'extrémité d'une stèle décrit chaque jour un arc de section conique, ce qui devint entre ses mains la base de nouveaux principes de gnomonique. Il fait aussi dériver les propriétés des coniques de celles du cercle et de la considération du solide dans lequel ces courbes prennent naissance. Werner, de Nuremberg, avait déjà démontré par la même méthode quelques propriétés élémentaires des coniques, mais d'une façon moins étendue que Maurolycus. 

Borrel.
Né en 1492, et mort à Grenoble, en 1572, Jean Borrel (Johannes Buteo), inventa plusieurs instruments de mathématiques, qui furent brisés pendant les Guerres de religion, et lui-même fut obligé de fuir pour sa sûreté personnelle. Nous avons à mentionner de lui : 

1°Logistica (Lyon, 1559), petit traité d'arithmétique et d'algèbre où l'auteur suit l'exemple de Stifel, en représentant, dans les équations, par des lettres les inconnues de la question. Mais l'empire de l'habitude faisait encore rejeter par beaucoup d'autres, même par Cardan et Tartaglia, une idée si heureuse pour la facilité du calcul. 

2° De Quadratura circuli (Lyon, 1559). En faisant l'histoire de la quadrature du cercle, l'auteur réfute les paralogismes auxquels ce problème a donné lieu. Comme Regiomontanus, il attribue le rapport  aux Arabes; il remarque aussi qu'on s'écarte des données d'Archimède, extra limites Archimedis, en représentant la circonférence par la racine carrée de 10 (le diamètre étant pris pour l'unité). 

Pour la multiplication, l'auteur emploie une méthode qui parait avoir été très usitée au Moyen âge et au XVI^e siècle; elle consistait à écrire le produit de chaque chiffre du multiplicande par chaque chiffre du multiplicateur, en plaçant séparément, dans les deux cases triangulaires d'un carré, les chiffres des unités et des dizaines. Cette méthode s'appelait, dit-il, indienne, parce qu'elle avait été indiquée par Ganesa dans ses commentaires sur le Lilavati de Bhaskara (Les mathématiques en Inde) Dans ce même traité, l'auteur fait usage d'un théorème de Ptolémée, relatif au triangle coupé par une transversale, pour démontrer géométriquement la règle arithmétique des six quantités. 

Dans cette règle, que Cardan attribue à Al-Kindi, il s'agit de résoudre cette question : Le rapport d'une première quantité à une seconde, étant composé du rapport d'une troisième à une quatrième, et du rapport d'une cinquième à une sixième, trouver le rapport d'une quelconque des seconde, troisième et cinquième quantités à une quelconque des trois autres. Ainsi avec a, b, c, d, e, f, on a a/b = c/d-e/f et on demande d'en conclure le rapport d'une des trois quantités b, c, e, à l'une des trois autres, a, d, f.

Xylander.
Né à Augsbourg, le 26 décembre 1532, et mort le 10 février 1576 à Heidelberg où il était professeur depuis 1558, Guillaume Xylander fit paraître en 1556 une édition des oeuvres de Psellus, en 1562 une édition des Eléments d'Euclide, en 1575 une édition de l'arithmélique de Diophante; il composa aussi quelques ouvrages de moindre importance qui furent réunis et publiés, en 1577.

Commandin.
Né en 1509 à Urbino et mort dans la même ville le 3 septembre 1575, Federigo Commandin publia en 1558 une traduction des oeuvres d'Archimède; en 1566 des extraits d'Apollonius et de Pappus; en 1572 une édition des Elements d'Euclide ; et en 1574 des extraits choisis d'Aristarque, de Ptolémée, d'Héron et de Pappus, qu'il fit suivre de commentaires.

Peletier.
Né au Mans le 25 juillet 1517 et mort à Paris en juillet 1582, Jacques Peletier avait des connaissances très variées. Il écrivit, outre un commentaire sur les six premiers livres d'Euclide (In Euclidis elementa geometrica demonstrationurn libri VI; Lyon, 1557), sur l'Arithmétique (Poitiers, 1551), et sur l'Algèbre (Lyon, 1554). Dans ce dernier traité, il dit fort judicieusement, à propos de l'origine de l'algèbre, « que c'est là une de ces choses qui, loin de devoir leur invention à un seul auteur, n'ont pris règle, forme et ordre, qu'après un longtemps de circuitions, d'intermissions et de continuelles exercitations d'esprit. » Ses ouvrages géométriques sont : Disquisitiones geometricae (Lyon, 1567), et de l'Usage de la géométrie (Paris, 1573). La plupart des résultats de Stifel et de Cardan se trouvent. dans le premier de ses ouvrages.

Peletier eut avec Clavius une vive polémique, renouvelée par la suite par d'autres mathématiciens, au sujet de l'angle de contingence, angle formé par une ligne droite (tangente) qui touche un cercle ou une courbe quelconque. Peletier soutenait que ce n'est pas là un véritable angle; tandis que Clavius considérait cet angle comme réel, mais d'une nature différente de l'angle rectiligne, sur ce qu'on démontre que le plus grand angle de contingence est moindre que le plus petit angle rectiligne. La querelle venait de ce que, de part et d'autre, on ne s'entendait pas sur l'idée des infiniment petits, qui commençait à s'introduire dans la géométrie. En effet, si l'on admet que la tangente se confond avec le côté évanescent ou infiniment petit de la courbe, il n'y aura pas d'angle en ce point de contact, car deux droites parallèles ne font point d'angle.

Pitiscus.
Barthelemäus Pitiscus (1561-1613) était professeur de mathématiques à Heidelberg. Il publia en 1599 sa Trigonométrie : elle contient les expressions pour sin (A ± B) et cos (A ± B), en fonction des rapports trigonométriques des angles A et B.

Vers cette époque également plusieurs livres classiques parurent, qui contribuèrent à la classification méthodique des sujets, s'ils n'en étendirent pas les limites. Tous pouvons mentionner en particulier ceux de Ramus et de Bombelli.

Ramus.
Pierre de la Ramée, dit Ramus (1515-1572) fit ses études à l'Université de Paris. C'est dans cette ville qu'il obtint une chaire au Collège de France, où il fonda, avec ses propres deniers, une chaire de mathématiques, qui fut plus tard illustrée par Roberval. Il eut pour successeur dans son enseignement Maurice Brassius, auteur d'une trigonométrie fort estimée de son temps. Outre quelques ouvrages sur la philosophie, il écrivit des traités sur l'arithmétique, l'algèbre, la géométrie (inspirée d'Euclide), l'astronomie (basée sur les travaux de Copernic) et la physique qui furent longtemps regardés comme les meilleurs classiques sur ces sujets. Ils ont été réunis dans une édition de ses oeuvres publiées à Bâle en 1569.

Admirateur des anciens, Ramus traduisit les Éléments d'Euclide, adopta l'un des premiers le système de Copernic, et se déclara, en physique et en médecine, pour la méthode expérimentale. Ses traités de géométrie, d'arithmétique et d'algèbre eurent de nombreuses éditions. Ses Scholae mathematicae, en trente et un livres (Bâle, 1569), servirent longtemps de guide pour l'enseignement des mathématiques.

Un fait digne de remarque, c'est qu'à l'époque de Ramus les mathématiques étaient en grande faveur, non seulement auprès des philosophes et des humanistes, mais surtout auprès des médecins, témoin Fernel, qui se fit connaître par sa mesure d'un degré terrestre du méridien, ainsi que par son traité de Proportionibus, etc.; Paris, 1528.

Bombelli. 
Presque immédiatement après l'apparition du grand ouvrage de Cardan, Raffaelo Bombelli publia en 1572 une algèbre qui est une exposition méthodique de ce qu'on connaissait alors de cette discipline. Dans la préface, il trace l'historique de la question et fait allusion à Diophante qui, malgré la notice de Regiomontanus, était encore inconnu en Europe. Il discute les radicaux, réels et imaginaires. Il traite également la théorie des équations et montre que, dans le cas irréductible d'une équation cubique, les racines sont toutes réelles; il fait remarquer que le problème de la trisection d'un angle se ramène à la solution d'une équation cubique. Enfin il donne une collection abondante de problèmes.

L'ouvrage de Bombelli est à noter à cause de l'emploi de symboles qui préfigurent la notation par indices. Marchant sur les traces de Stifel, il introduisit pour désigner la quantité inconnue, son carré, son cube, et ainsi de suite, les symboles ... Par conséquent il écrivait x² + 5x - 4 comme il suit : .

En 1586, Stevin employait d'une façon semblable ..., et avait suggéré, bien qu'il n'en ait pas fait usage, une notation correspondante pour les indices fractionnaires. Il aurait écrit comme il suit l'expression précédente : .

Mais, que ces symboles fussent plus ou moins avantageux, ils n'étaient encore uniquement que des abréviations pour des mots, et étaient soumis à toutes les règles de la syntaxe. Ils constituaient simplement une sorte de sténographie permettant d'exprimer d'une façon concise les diverses périodes d'une solution et les résultats. Le premier perfectionnement fut la création de l'algèbre symbolique, dont le mérite revient principalement à Viète.

Scheubel.
Johannes Scheubel,  (1494-1570), plus connu sous le nom latinisé de Scheubelius, traduisit en allemand et commenta les VII^e, VIII^e et IX^e livres d'Euclide, traitant de l'arithmétique (1558). Mais il se fit surtout connaître par son traité de Numeris et diversis rationibus seu regulis computationis (Leipzig, 1545). Il y considère l'arithmétique moins comme un art que comme une science digne des méditations de tous les savants. Scheubel a contribué à répandre l'usage des symboles + et -.

Schöner.
Johann Schöner  (1477 - 1547), géographe et cosmographe, comme Scheubel, fut nommé en 1526 professeur de mathématiques à  Nuremberg. Nous mentionnons ici son nom parce qu'à son époque, les arithméticiens admettaient quatre espèces de nombres (les digiti, les articuli, les limites et les compositi), et que dans son Algorithmus demonstratus, il définit clairement ces mots. 

« Le digitus est, dit-il, tout nombre moindre que dix. L'articulus s'appelle tout nombre qui décuple le digitus, ou qui est le décuple du digitus, ou le décuple du décuple, et ainsi de suite jusqu'à l'infini. Les digiti et les articuli se distinguent des limites. La limite, limes, est un groupe de neuf nombres, qui peuvent être des digiti ou des multiples de digiti. Le nombre composé est une réunion de nombres de diverses limités, ou un nombre représenté par des figures. »

Adrien Romain. 
Adriaan van Roomen, plus connu sous le nom d'Adrien Romain (né à Louvain le 29 septembre 1561, mort à Mayence le 11 mai 1625), vint enseigner la médecine et les mathématiques à Louvain, après avoir étudié à Cologne et à Paris.

Son Uranographie (Uranographia sine Caeli descriptio), qu'il fit paraître en 1590, est un cours d'astronomie élementaire, rédigé au point de vue de la science d'alors. Dans la même année il avait publié sa méthode des Polygones (Idem mathematicae pars prima, sive Methodus polygonum, Louvain, 1590), qui contient le rapport de la circonférence d'un cercle à son diamètre, avec quinze décimales. Cette détermination, la plus exacte qu'on ait encore calculée, donne, le diamètre étant pris pour unité, à la circonférence du cercle la valeur de 3,141,592,653,589,793. Cette valeur, désignée depuis par  (initiale du mot grec periphereia = circonférence), a été reproduite dans beaucoup de livres de géométrie. Adrien Romain, Viète et Clavius eurent une vive controverse avec Joseph Scaliger qui prétendait avoir trouvé la quadrature du cercle, dans ses Cyclometrica elementa duo (Leyde, 1594).

Dans son Canon triangulorum sphaericorum (Mayence, 1609), A. Romain entreprit de simplifier la trigonométrie sphérique, en la réduisant à six problèmes, dont tous les autres ne sont que des cas particuliers. Selon la mode du temps, l'auteur du Canon avait proposé une question embarrassante à ses contemporains géomètres. Viète lui en envoya la solution; mais à son tour il proposait au géomètre belge « de mener un cercle tangent à trois cercles donnés ». A. Romain résolut le problème par l'intersection de deux hyperboles. Mais Viète lui lit observer, que cette solution n'avait pas la rigueur de la géométrie ancienne, et il en donna en même temps une autre, qui avait toute la précision désirée.

Adrien Romain fut le premier qui établit la formule usuelle donnant le développement de sin (A + B).

Van Ceulen.
Ludolph van Ceulen ou van Colen (1539 - 1610) enseigna les mathématiques à Leyde. Il fut un de ceux qui aimaient ardemment les joutes mathématiques. Ses deux principaux ouvrages, primitivement écrits en hollandais, furent traduits par Snellius; le premier a pour titre : Fundamenta arithmetica et geometrica, etc. (Leyde, 1615) ; le second : de Circulo et adscriptis liber, etc. (ibid., 1619). Les Fondements sont divisés en six livres; le premier expose la théorie de l'arithmétique et des quantités sourdes; le deuxième traite des constructions linéaires, dans le sens d'Euclide; le troisième, de la transformation et de la division des polygones; les quatrième, cinquième et sixième forment une collection de problèmes proposés, soit à l'auteur, soit à d'autres géomètres, et il en donne la solution. Dans le traité du Cercle, van Ceulen, aidé de son élève Cornelisz, a poussé la valeur de  jusqu'à la trentième décimale.

Metius.
Adriaan Metius (1571 - 1635), qui enseignait depuis 1598 les mathématiques à Franeker, s'occupa également, avec beaucoup d'ardeur, de la détermination, la plus approchée possible, du rapport de la circonférence au cercle. Outre divers ouvrages d'astronomie, il a laissé, en latin, un traité d'Arithmétique et un traité de Géométrie (Franeker, 1611).

Le développement de l'algèbre symbolique

Viète.
François Viète, dit Franciscus Vieta (1540-1603) eut une carrière de juriste, maisprès 1580, il consacra la plus grande partie de ses loisirs aux mathématiques, bien que son grand ouvrage In Artem Analyticam Isagoge dans  lequel il expliquait comment l'algèbre pouvait être appliquée à la résolution des problèmes de géométrie, ne fut pas publié avant. 1591.

Sa réputation comme mathématicien était déjà considérable, lorsque l'ambassadeur des Provinces-Unies fit remarquer un jour à Henri IV que la France ne possédait aucun géomètre capable de, résoudre un problème qui avait été proposé en 1593 par son compatriote Adrien Romain à tous les mathématiciens du monde et qui exigeait la solution d'une équation du 45^me degré. Le roi fit venir Viète et lui fit part du défi. Viète vit que l'inconnue de l'équation représentait la longueur de la corde d'un cercle (ayant l'unité pour rayon) sous-tendant un angle au centre égal à 2/45 et, au bout de quelques minutes, il fit remettre au roi deux solutions du problème écrites au crayon. Comme complément d'explication, nous devons ajouter que Viète avait antérieurement découvert comment on pouvait former sin au moyen de sin et cos. Viète à son tour proposa à Romain de construire un cercle tangent à trois cercles donnés. C'était le problème traité par Apollonius dans son De Tactionibus, livre perdu que Viète restitua par conjectures un peu plus tard. Romain résolut la question au moyen des sections coniques, mais ne put trouver une solution par la géométrie euclidienne. Viète donna une solution euclidienne, qui fit une telle impression. sur Romain vint à la Cour du roi de France, pour faire la connaissance de Viète, connaissance qui se transforma rapidement en une constante amitié.

François Viète.

Henri IV avait été vivement frappé de la haute sagacité de Viète. Une autre circonstance donna à celui-ci l'occasion de la manifester d'une manière brillante.
Les Espagnols se servaient à cette époque d'un chiffre, contenant environ 600 caractères, qui étaient périodiquement changés et qu'il était impossible, croyaient-ils, de déchiffrer. Une dépêche ayant été interceptée, le roi la donna à Viète en lui demandant d'essayer de la lire et de trouver la clef du chiffre. Viète y parvint, et pendant deux ans les Français utilisèrent fort avantageusement cette découverte, durant la guerre qui était alors engagée. Pilippe II était tellement convaincu que le chiffre ne pouvait être découvert, que, lorsqu'il eut constaté que ses plans étaient connus, il se plaignit au pape de ce que les Français avaient recours à la sorcellerie « contrairement à la pratique de la foi chrétienne. »

Viète écrivit de nombreux ouvrages sur l'algèbre et la géométrie. Les plus importants sont : le In Artem Analyticam Isagoge, Tours 1591 : le Supplementum Geometriae et une collection de problèmes de géométrie, Tours 1593; et le De Numerosa Potestatum Resolutione, Paris,1600 : tous ne furent imprimés qu'a un petit nombre d'exemplaires pour son usage privé, mais ils furent réunis par F. Van Schooten et publiés en un volume à Leyde en 1646. Viète  écrivit aussi le De AEquationum Recognitione et Emendatione qui fut publié en 1615, après sa mort, par Alexandre Anderson.

Le In Artem est le plus ancien ouvrage sur l'algèbre symbolique. Il y introduisit l'usage des lettres pour représenter à la fois les quantités (positives) connues et inconnues, une notation pour les puissances, et il insistait sur l'avantage de n'opérer que sur des équations homogènes. A cet ouvrage un appendice intitulé Logistice speciosa fut ajouté; il traitait de l'addition et de la multiplication des quantités algébriques et de l'élévation d'un binôme à ses diverses puissances jusqu'à la sixième. Viète laisse supposer qu'il savait comment former les coefficients de ces six développements en se servant du triangle arithmétique, comme Tartaglia l'avait déjà fait; mais Pascal donna la règle générale pour former ces coefficients pour une puissance quelconque, et Stifel avait déjà fait connaître comment on pouvait former le développement de (I + x)ⁿ lorsque les coefficients du développement de (I - x) ^n-1 étaient connus; Newton fut le premier qui donna l'expression générale du coefficient de xp dans le développement de (I ± x)ⁿ. Un autre appendice, connu sous le nom de Zetetica, sur la résolution des équations, fut, par la suite, ajouté au In Artem.

Le In Artem est remarquable à cause de deux perfectionnements qu'on y trouve concernant la notation algébrique, bien que probablement Viète en ait pris l'idée dans d'autres auteurs.

L'un de ces perfectionnements consiste dans la représentation des quantités connues par les consonnes B, C, D,... etc., et des quantités inconnues par les voyelles A, E, I, etc. Il lui était possible de la sorte d'introduire dans un problème un certain nombre de quantités inconnues; mais, sur ce point particulier, il semble avoir été devancé par Jordanus Nemorarius et par Stifel. L'usage actuel des lettres du commencement de l'alphabet a, b, c, etc, pour représenter les quantités connues et des lettres de la fin de l'alphabet, x, y, z, ... etc.. pour désigner les inconnues, a été introduit par Descartes en 1637.

Voici en quoi consiste le second perfectionnement; jusqu'à cette époque on avait l'habitude d'introduire de nouveaux symboles pour représenter le carré, le cube, etc., des quantités figurant déjà dans les équations; ainsi si l'inconnue x était désignée par R ou N, le carré x² se désignait par Z ou C ou Q, le cube x³ par C ou K, etc. Aussi longtemps qu'il en fut ainsi, le principal avantage de l'algèbre consistait à présenter une exposition concise des résultats en opérant graduellement. Mais quand Viète fit usage de la lettre A pour indiquer la quantité inconnue x, il employait quelquefois A quadratus, Acubus..., pour représenter x², x³..., ce qui permettait de voir aussitôt la relation existant entre ces diverses puissances; et plus tard les puissances successives de A furent communément désignées parles abréviations Aq, Ac, Aqq, etc. Ainsi Viète aurait écrit l'équation 3BA² - DA + A³ = Z ainsi :

B 3 in A quad. - D plano in A + A cubo aequatur Z solido.

Ces deux perfectionnements étaient à peu près indispensables pour aider aux progrès ultérieurs de l'algèbre. Pour les deux, Viète avait été devancé, mais il eut la bonne fortune en en faisant saisir l'importance dans un style emphatique, de trouver le moyen de les faire connaître d'une façon générale à une époque ou l'opinion était disposée à les adopter.

Le De Aequationumn Recognitione et Emendatione traite principalement de la théorie des équations. Viète y montra que le premier membre d'une équation algébrique (x) = 0 peut être transformé en facteurs linéaires, et il expliqua comment les coefficients de x peuvent être exprimés en fonction des racines. Il donna également le moyen de former, à l'aide d'une équation donnée, une autre équation ayant pour racines celles de la première augmentées d'une quantité donnée ou multipliées par une quantité donnée et il utilisa cette méthode pour se débarrasser du coefficient de x dans l'équation du second degré et du coefficient de x² dans une équation cubique, ce qui lui permit d'arriver à la solution algébrique générale de ces deux sortes d'équation.

Sa solution de l'équation cubique est la suivante : Il réduit d'abord l'équation à la forme x³ + 3a²x = 2b³. Posant ensuite x = a²/y - y, il obtient par substitution y⁶ + 2b³y³ = a⁶, c'est-à-dire une équation quadratique en y³. II peut alors trouver y et déterminer x.

Sa solution d'une équation biquadratique est semblable à celle de Ferrari, que nous connaissons; la voici en substance : il commence par se débarrasser du terme en x³, et l'équation se trouve alors ramenée à la forme x⁴ + a²x² + b³x = c⁴. Il fait ensuite passer les termes en x² et x dans le membre de droite, puis ajoutant de part et d'autre x²y² + 1/4 y⁴, l'équation devient

(x² + 1/2 y²) = x² (y²-a²) - b³x + 1/4 y⁴ +c⁴

Le De Numerosa Potestatum Resolutione traite de la résolution de nombreuses équations numériques. Dans cet ouvrage se trouve une méthode pour déterminer les valeurs approchées des racines positives, mais elle est prolixe et de peu d'usage, bien que son principe (qui est semblable à celui sur lequel s'appuie la règle de Newton) soit exact. Les racines négatives sont invariablement rejetées. Cet ouvrage est à peine digne de la réputation de Viète.

Les recherches trigonométriques de Viète sont comprises dans divers traités réunis dans l'édition de Van Schooten. Outre quelques tables trigonométriques, il donna l'expression générale du sinus (ou corde) d'un angle en fonction du sinus et du cosinus de ses sous-multiples. Delambre estime que ces recherches forment le complément du système trigonométrique arabe.

Nous pouvons en conclure que depuis ce temps les résultats de la trigonométrie élémentaire étaient connus des mathématiciens. Viète étudia également la théorie des triangles sphériques rectangles.

Viète a démontré que les problèmes de la trisection de l'angle et de la duplication du cube dépendent de la résolution d'une équation cubique. Il eut en 1594 avec Clavius une controverse au sujet de la réforme du calendrier, mais dans cette circonstance il ne semble pas avoir été bien conseillé.

Les travaux de Viète en géométrie sont remarquables sans présenter une grande originalité. Il appliqua l'algèbre et la trigonométrie dans ses recherches sur les propriétés des figures. Il insista, comme nous l'avons déjà dit, sur ce fait qu'il était avantageux d'opérer toujours sur des équations homogènes, de telle sorte que, si l'on donnait un carré ou un cube, on devait les représenter par des expressions telles que a² ou b³, et non par des termes tels que m ou n, qui n'indiquent pas les dimensions des quantités qu'ils représentent. Il eut une vive dispute avec Scaliger au sujet de l'ouvrage sur la quadrature du cercle publié par ce dernier et il réussit à montrer l'erreur dans laquelle son rival était tombé. Il établit lui-même une relation curieuse entre l'aire du carré et celle du cercle circonscrit et montra que ces deux surfaces sont entre elles comme le produit infini

est à 1

C'est là un des plus anciens essais tentés pour arriver à une valeur de  au moyen d'une série infinie.

Viète connaissait bien les écrits des géomètres grecs. Ce fut lui qui fit la première tentative, dans laquelle il devait trouver des imitateurs, de reconstituer des travaux perdus. Il restitua l'ouvrage perdu d'Apollonius : De Tactionibus.

Girard.
Les résultats obtenus par Viète en trigonométrie et dans la théorie des équations furent développés par Albert Girard, mathématicien hollandais, né en Lorraine en 1595 et mort le 9 décembre 1632.

En 1626 Girard publia à la Haye un court traité de Trigonométrie, auquel étaient annexées des tables des valeurs des fonctions trigonométriques. Cet ouvrage contient l'exemple le plus ancien de l'usage des abréviations sin., tan., sec. pour sinus, tangente et sécante.

Les triangles supplémentaires en trigonométrie sphérique sont également étudiés; leurs propriétés semblent avoir été découvertes à peu près en même temps par Girard et Snell. Girard donna aussi l'expression de l'aire d'un triangle sphérique en fonction de l'excès sphérique, découverte que Cavalieri fit de son côté. En 1627 Girard fit paraître une édition de la géométrie de Marolois avec de nombreuses additions.

Les recherches algébriques de Girard sont contenues dans l'ouvrage Invention nouvelle en Algèbre publié à Amsterdam en 1629 : il con tient l'exemple le plus ancien de l'usage des crochets; une interprétation géométrique du signe négatif; la constatation que le nombre des racines d'une équation est égal à son degré; la reconnaissance distincte des racines imaginaires; le théorème connu sous le nom de règle de Newton pour trouver la somme des puissances semblables des racines d'une équation, et probablement aussi, la remarque que le premier membre d'une équation algébrique  (x) = 0 peut être décomposé en facteurs linéaires. Les recherches de Girard, ignorées de la plupart de ses contemporains, n'exercèrent aucune influence appréciable sur le développement des mathématiques.

Napier, Briggs et l'invention des Logarithmes
Napier.
John Napier ou Néper (1550-1617) s'est signalé en son temps comme controversiste politique et religieux, et n'a pratiqué les mathématiques que comme un loisir. Sa contribution à cette discipline n'en est pas pour autant négligeable. Aussitôt que les exposants furent d'un usage commun en algèbre, l'introduction des logarithmes devait naturellement suivre; mais Napier raisonna sans employer, pour faciliter ses recherches; aucune notation symbolique et l'invention des logarithmes est le résultat d'efforts tentés pendant plusieurs années dans le but d'abréger les procédés de la multiplication et de la division.

Il est vraisemblable que l'attention de Napier fut attirée sur ce sujet, en voyant le vif plaisir que semblaient prendre quelques-uns de ses contemporains, à se surpasser les uns les autres dans les développements donnés à leurs multiplications et à leurs divisions. Les tables trigonométriques de Rhéticus, publiées en 1596 et 1613, avaient été calculées d'une manière très laborieuse : Viète lui-même se plaisait à effectuer des calculs arithmétiques, dont beaucoup exigeaient des journées d'un travail ardu, et dont souvent les résultats ne servaient à rien d'utile; L. Van Ceulen (1539-1610) consacra en réalité sa vie à calculer une valeur numérique approchée de et finalement en 1610 il en obtenait une exacte jusqu'à 35 chiffres décimaux pour citer un dernier exemple, P. A. Cataldi (1548-1626), qui est principalement connu pour son invention en 1613 des fractions continues, passa des années entières à effectuer des calculs numériques.

En ce qui concerne les autres travaux de Napier, nous pouvons encore mentionner que dans sa Rabdologia, ouvrage publié en 1617, il faisait connaître une forme perfectionnée de baguettes au moyen desquelles on pouvait trouver mécaniquement le produit de deux nombres ou le quotient de leur division. Il inventa aussi deux autres baguettes appelées « virgule » avec lesquelles on pouvait extraire les racines carrée et cubique. Nous pourrions ajouter qu'en trigonométrie sphérique il découvrit certaines formulés connues sous le nom de analogies de Neper et appelées « la règle des parties circulaires » pour la résolution des triangles sphériques rectangles.

Briggs. 
Le nom de Briggs est lié d'une façon inséparable à l'histoire des logarithmes. Henry Briggs (1561-1630)  fut choisi en 1596 pour occuper la chaire de géométrie fondée par Gresham, et en 1619 ou 1620 obtint la chaire de Savile à Oxford, et l'occupa jusqu'à sa mort le 26 janvier 1631. Il peut être intéressant d'ajouter que la chaire de géométrie fondée par Sir Thomas Gresham fut la plus ancienne qui ait été créée dans la Grande Bretagne. Environ vingt ans plus tôt, Sir Henri Savile avait donné à Oxford des conférences libres sur la géométrie grecque et les géomètres grecs, et en 1619 il dota les chaires de géométrie et d'astronomie de cette université qui partent encore son nom. A la fois à Londres et à Oxford, Briggs fut le premier qui occupa la chaire de géométrie. A Oxford il commença ses leçons par la neuvième proposition du premier livre d'Euclide, Savile n'ayant pas été capable de pousser ses conférences plus loin. A Cambridge, la chaire Lucasian fut créée en 1663 et les plus anciens professeurs qui l'occupèrent furent Barrow et Newton.

L'adoption presque immédiate en Europe des logarithmes, pour les calculs astronomiques ou autres, est due principalement à Briggs qui entreprit le pénible travail de calculer et de préparer des tables de logarithmes. Il réussit à convaincre Kepler de l'avantage que présentait la découverte de Napier, et le développement des logarithmes fut rendu plus rapide par la propagande et la réputation de Kepler, qui les mit en vogue en Allemagne par ses tables de 1625 et de 1629, tandis que Cavalieri en 1624 et Edmond Wingate en 1626 rendaient respectivement le même service aux mathématiciens italiens et français.

Briggs se signala aussi en vulgarisant la méthode de division qui est encore généralement employée de nos jours.

Harriot. 
Thomas Harriot (1560-1621) travailla beaucoup à étendre et à codifier la théorie des équations. La majeure partie des propositions données par Viète se trouvent dans les écrits d'Harriot, mais on ne sait si elles ont été decouvertes par lui indépendamment des travaux de Viète, ou s'il en avait connaissance. Dans tous les cas il est probable que ce dernier n'avait pas complètement démontré tout ce qui est contenu dans les propositions énoncées. Quelques conséquences de ces propositions avec des développements et une exposition systématique de la théorie des équations furent données par Harriot dans son ouvrage Artis Analytica Praxis imprimé en 1631. Cet ouvrage est plus analytique qu'aucune autre algèbre antérieure et marque un progrès à la fois dans le symbolisme et dans la notation, mais les. racines négatives et imaginaires sont rejetées. Il fut beaucoup lu et doit être considéré comme un de ceux qui ont le plus contribué à répandre les méthodes analytiques.

Harriot, le premier fit usage des signes > et < pour représenter « plus grand que » et « plus. petit que ». Quand il désignait la quantité inconnue par a, il écrivait son carré aa, son cube aaa, et ainsi de suite. C'est là un perfectionnement bien net de la notation de Viète. Le même symbolisme était employé par Wallis jusqu'en 1685, mais concurremment avec la notation moderne des exposants qui a été introduite par Descartes.

Nous croyons inutile de faire allusion aux autres recherches d'Harriot qui ont comparativement peu de valeur.

Anderson.
Alexander Anderson, contemporain et compatriote de Harriot, s'occupa de questions d'analyse géométrique dans son Supplementum Apollonii redivivi, 1612, et surtout dans un petit opuscule intitulé : Animadversionis in Franciscum Vietam a Clemente Cyriaco nuper edita brevis Diakrisis, Paris, 1617. L'auteur y appelle
porisma un problème local, où il s'agit de trouver le lieu des sommets des triangles qui, ayant même base, ont leurs deux autres côtés dans un rapport constant. Mersenne fait, dans son livre la Vérité des sciences (1625), un grand éloge d'Anderson, qui avait étudié à fond Archimède et Apollonius, et préparé plusieurs ouvrages (qui n'ont pas vu le jour), pour suppléer à ceux des anciens qui ne nous sont pas parvenus.

Oughtred.
Parmi ceux qui contribuèrent à faire adopter en Angleterre ces divers perfectionnements, et ces additions variées algorithmiques et algébriques, il faut citer William Oughtred (1574-1660). Son ouvrage Clavis Mathematicae publié en 1631 est un bon livre classique méthodique sur l'arithmétique, qui contient tout ce qui étais alors connu sur le sujet. Il y introduisit le symbole X pour la multiplication. On y trouve aussi le symbole :: pour indiquer une proportion, antérieurement une proportion telle que a : b = c : d était généralement écrite a - b - c - d; il l'écrivait a. b :: c. d. Wallis dit que quelques personnes trouvèrent le livre défectueux à cause du style, mais d'après lui, ceux qui pensaient ainsi faisaient preuve de peu de compétence, car dans Oughtred « les phrases sont abondantes mais non redondantes ». Pell fait une remarque à peu près semblable.

Oughtred écrivit aussi un traité de trigonométrie, publié en 1657, et. dans lequel les abréviations pour sinus, cosinus, etc, étaient employées. C'était là réellement un perfectionnement important mais les ouvrages de Girard et d'Oughtred, dans lesquels ces abréviations figurent, furent négligés et bientôt oubliés, et ces simplifications dans l'écriture des fonctions trigonométriques ne furent généralement adoptées que lorsqu'Euler les eut introduites à nouveau.

Nous pouvons nous résumer en disant qu'à partir de ce moment l'arithmétique, l'algèbre et la trigonométrie élémentaires ont été traitées d'une manière qui, en substance, ne diffère pas de celle exposée dans nos ouvrages contemporains; de plus les perfectionnements introduits dans la suite consistèrent en additions et non en remaniements ayant pour but de présenter ces sciences sur de nouvelles bases.

Développement de la mécanique et des méthodes expérimentales

Stevin.
Simon Stevin (1548 - 1620) était surtout connu de ses contemporains par ses ouvrages sur les travaux de fortifications et sur l'art militaire. Il était également populaire à cause de l'invention d'une voiture mise en mouvement à l'aide de voiles ; elle roulait sur le bord de la mer portant vingt-huit personnes, et dépassait facilement un cheval galopant à côté : le modèle de cette voiture a été détruit par les Français en 1802 lorsqu'ils envahirent la Hollande. C'est principalement à l'influence de Stevin que les Hollandais et les Français doivent l'établissement d'un système convenable de comptabilité publique.

Nous avons déjà fait allusion â l'introduction dans son Arithmétique, publiée en 1585, des exposants pour marquer la puissance â laquelle on élève une quantité : par exemple il écrit 3x² - 5x + 1 comme il suit : . Sa notation pour les fractions décimales présentait un caractère identique. Plus tard il suggéra l'emploi des exposants fractionnaires (mais non négatifs). Dans le même ouvrage il donne l'idée d'un système décimal de poids et mesures.

Il publia également une géométrie ingénieuse, bien qu'elle ne contienne que des résultats déjà antérieurement connus : on y trouve énoncés quelques théorèmes de perspective.

C'est cependant son ouvrage Statique et Hydrostatique publié (en, flamand) à Leyde, en 1586, qui a fait sa réputation. Dans ce livre il énonce la règle du triangle des forces, théorème qui, d'après quelques-uns, aurait été trouvé pour la première fois par Leonard de Vinci. Stevin le regarde comme la proposition fondamentale de son ouvrage; antérieurement à la publication de cet ouvrage la statique reposait sur la théorie du levier; puis on montra la possibilité de représenter les forces par des lignes droites, ce qui permit de ramener plusieurs théorèmes à des propositions géométriques, et en particulier, d'obtenir ainsi une démonstration du parallélogramme des forces (proposition équivalente à celle du triangle des forces). Stevin manque de clarté dans l'arrangement de ses diverses propositions ou dans leurs conséquences logiques, et l'exposition nouvelle du sujet ne fut définitivement arrêtée que lors de la publication, en 1687, des ouvrages de Varignon sur la mécanique. Stevin détermina également la force qu'il est nécessaire de faire agir le long de la ligne de plus grande pente pour maintenir un corps pesant sur un plan incliné - problème dont la solution avait été longtemps discutée.

Plus tard il établit la distinction entre l'équilibre stable et instable. En hydrostatique il examina les questions relatives à la pression exercée par un fluide, et donna l'explication du paradoxe dit hydrostatique.

Sa méthode pour déterminer la composante d'une force suivant une direction donnée, dans le cas du poids reposant sur un plan incliné fournit un exemple qui mérite d'être cité.

Il prend un coin ABC dont la base AC est horizontale (et dont les côtés BA, BC sont dans le rapport de 2 à 1). Un fil reliant un certain nombre de petits poids égaux et équidistants est placé  sur le coin comme le représente la figure ci-dessous, de telle sorte que le nombre des poids reposant sur BA est au nombre de ceux reposant sur BC dans la même proportion que BA à BC (ceci est toujours possible si les dimensions du coin sont choisies convenablement en plaçant quatre poids sur BA et deux sur BC).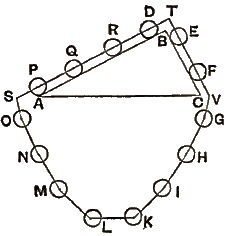 

Nous pouvons, sans rien enlever à la force de son raisonnement, remplacer les poids par une chaîne d'un poids uniforme TSLVT. Il fait observer qu'une pareille chaîne se maintiendra au repos, car s'il n'en était pas ainsi, on pourrait obtenir un mouvement perpétuel. Ainsi l'effet dans la direction BA du poids de la portion TS de la chaîne doit équilibrer l'effet dans la direction BC du poids de la portion TV de la chaîne. Bien entendu la direction BC peut être verticale et, dans ce cas, le raisonnement précédent revient à dire que l'effet suivant la direction BA du poids de la portion de chaîne reposant sur ce côté est diminué dans le rapport de BC à BA; en d'autres. termes, si un poids P s'appuie sur un plan incliné faisant avec l'horizon un angle , la composante de P suivant la ligne de plus, grande pente est égale à P sin.

Stevin était quelque peu dogmatique dans ses raisonnements, et ne permettait à personne d'avoir un avis contraire, « et quant à ceux » dit-il dans un endroit « qui ne peuvent comprendre cela, que l'auteur de la nature ait pitié de leurs yeux infortunés, car la faute n'en est pas au raisonnement, mais à la vue qui leur manque et que nous ne pouvons leur donner ».

Guldin.
Habakkuk Guldin, né à Saint-Gall, le 12 juin 1577 et mort à Graetz le 3 novembre 1643, était de descendance Juive mais fut élevé dans le protestantisme : il se convertit au catholicisme romain et entra dans l'ordre des Jésuites, où il prit le nom chrétien de Paul. C'est à lui que les collèges Jésuites de Rome et de Graetz doivent leur réputation. Les deux théorèmes connus sous le nom de Pappus furent publiés par Guldin dans le quatrième livre de son De Centro Gravitatis, Vienne, 1635-1642. Non seulement Guldin emprunta à Pappus sans le mentionner les règles en question, mais encore (suivant Montucla) sa démonstration est erronée, bien que les applications qu'il en fait à la détermination des volumes et des surfaces de certains solides soient exactes. Cependant ces théorèmes étaient inconnus antérieurement et ils excitèrent un intérêt considérable.

Wright.
Nous pouvons également citer ici Edouard Wright, qui mérite d'être mentionné pour avoir établi l'art de la navigation sur des bases scientifiques. Wright naquit à Norfolk vers 1560 et mourut en 1615. Il fit ses études au Collège Caius à Cambridge et devint par la suite fellow de cette école. Il paraît qu'il fut bon marin et il avait un talent spécial pour la construction des instruments. Vers 1600 il fut choisi pour faire des conférences mathématiques par la Compagnie des Indes Orientales; il s'établit alors à Londres, et peu après fut désigné pour être le précepteur de mathématiques de Henry, Prince de Galles, le fils de Jacques Ier. Comme exemple de son habileté en mécanique, nous citerons un planétaire de sa construction au moyen duquel il était possible d'annoncer les éclipses et qui a été montré comme curiosité à la Tour de Londres au moins jusqu'en 1675.

Dans les cartes en usage avant Gerard Mercator, le degré, qu'il fût en longitude ou en latitude, était représenté dans tous les cas par la même longueur, et la route que devait suivre un navire était marquée par une ligne droite joignant les ports de départ et d'arrivée. Mercator avait vu qu'on était conduit ainsi à des erreurs considérables et avait compris que pour rendre exacte cette façon d'indiquer la route d'un navire, la longueur assignée sur la carte à un degré de latitude devait aller en croissant en
même temps que la latitude augmentait. Partant de ce principe, il avait construit empiriquement quelques cartes marines qui furent publiées vers 1560 ou 1570 ; Wright se proposa l'étude du problème et chercha à établir la théorie sur laquelle devait être basé le tracé de ces cartes; il réussit à trouver la loi d'une échelle de proportion bien que, rigoureusement parlant, sa règle ne s'applique exactement qu'aux petits arcs seulement.

En 1599 Wright publia son ouvrage Certain Errors in Navigation Detected and Corrected, dans lequel il expliquait la théorie et insérait une Table des parties du méridien. Cet ouvrage révèle des connaissances géométriques très étendues. Dans le cours de l'ouvrage il donne la déclinaison de trente deux étoiles, explique les phénomènes de l'inclinaison, de la parallaxe, de la réfraction, et ajoute une table des déclinaisons magnétiques; il suppose la terre immobile. L'année suivante, il fit paraître quelques cartes construites d'après ces principes et sur lesquelles le point de l'Australie le plus au Nord est indiqué : la latitude de Londres est prise égale à 51° 32'.

Snellius.
Willebrord Snell van Roijen, dit Snellius (1591-1626), employa toute sa vie, bien courte, à cultiver les sciences mathématiques. C'était un enfant prodige  et on raconte qu'à l'âge de douze ans il connaissait tous les ouvrages classiques de mathématiques de son temps; à dix-sept ans il essaya de restituer le traité perdu d'Apollonius de Sectione determinata (1608), et à l'âge de vingt-deux, il succéda à son père, Rodolphe Snellius, auteur de l'Apollonius batavus (Leyde, 1597), dans la chaire de mathématiques à l'université de Leyde. D'après le témoignage de Vossius et de Huygens, il trouva, avant Descartes, la  loi de la réfraction. Dans son Eratosthenes batavus (Leyde, 1617) il donne la méthode à employer pour mesurer un arc de méridien, méthode qui a servi depuis à tous les géomètres qui se sont occupés de cette question. Un ouvrage posthume de Snellius (Doctrinae triangulorum canonicae libri IV, Leyde, 1627) renferme la découverte du triangle supplémentaire (résultant de la doctrine de transformation des triangles sphériques due à Viète), et des remarques à l'appui de la loi de la dualité.

Byrge.
Juste Byrge ou Joost Bürgi (1549-1632) avait aidé Guillaume IV, landgrave de Hesse, dans ses travaux astronomiques. Après la mort de son protecteur, il devint mathématicien de l'empereur d'Allemagne, Rodolphe II, et cette position lui permit de continuer ses travaux. Byrge est l'inventeur d'un compas de proportion fort simple; mais c'est à tort qu'on lui attribue l'invention des logarithmes. Ses Tables progressives, arithmétiques et géométriques, dont il n'a paru, en 1620, que les sept premières feuilles, depuis longtemps introuvables, sont de deux ans postérieures à Napier.

Kepler.
Johannes Kepler (1571 -1630) doit être compté au nombre des plus grands mathématiciens, bien qu'il ait consacré tout son temps presque exclusivement à l'astronomie. Il nous a laissé deux ouvrages de mathématiques très remarquables, dont l'un a trait aux logarithmes, et l'autre à la stéréométrie. Le premier a pour titre Chilias logarithmorum, Linz, 1622; le second : Stereometria doliorum vinariorum, ibidem, 1605.

L'invention des logarithmes n'ayant pas été aussi favorablement accueillie sur le continent qu'en Angleterre, Kepler essaya le premier de la mettre à la portée de tout le monde dans sa Chiliade des logarithmes. C'est encore lui qui, l'un des premiers, introduisit dans le langage géométrique l'idée de l'infini, comme l'atteste sa Nouvelle Stéréométrie des tonneaux (Nova Stereometria doliorum; accessit stereometriv Archimedeae supplementum; 1615, in-fol.). Ce petit traité, trop peu connu, Kepler le composa à l'occasion d'une querelle avec un marchand de vin. 

« Le cercle n'est, dit-il, que le composé d'une infinité de triangles, dont le sommet est au centre et dont les bases forment la circonférence; le cône est composé d'une infinité de pyramides appuyées sur les triangles infiniment petits de sa base circulaire et ayant leur sommet commun avec celui du cône, tandis que le cylindre de même base et de même hauteur est formé d'un pareil nombre de petits prismes appuyés sur les mêmes bases et ayant même hauteur qu'elles. »

1° Decrementa perpendicularium sunt maxima apud A; minora igitur erunt apud B; 

2° Ubi decrementa altitudinum praecipitantur per omnes proportiones in infinitum crescentibus proportionum augmentis, ibi incrementa quadratorum magis magisque decrementa et incrementa proportionum decrescunt.

Ainsi, en cherchant, par des considérations géométriques, l'expression du côté de l'heptagone régulier inscrit au cercle, en fonction du rayon, il arrive à cette équation-:

7 -14ij +7iiij - 1vj, aeque valent nihilo, 

7-14x² + 7x⁴ -x⁶ = 0,

« La valeur de la racine d'une telle équation, ajoute Kepler, n'est pas unique; car il y en a deux pour le pentagone, trois pour l'heptagone, quatre pour l'ennéagone, et ainsi de suite [...]. Les trois racines de l'heptagone sont les côtés de trois heptagones différents, qu'on peut concevoir inscrits dans le même cercle. »