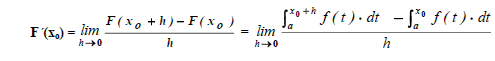|
En
termes généraux, une application est un moyen d'associer d'une
manière unique tous les éléments d'un ensemble donné, appelé
son domaine de définition, à des éléments de ce même ensemble ou d'un
autre ensemble ( Ensembles
et relations). Lorsque les éléments ainsi mis en relation sont des
nombres, ont donne généralement à l'application concernée le
nom de fonction. Ensembles
et relations). Lorsque les éléments ainsi mis en relation sont des
nombres, ont donne généralement à l'application concernée le
nom de fonction.
 Si
ce n'Ă©tait cet usage, qui peut avoir ses exceptions, les mots fonction
et application sont synonymes. Il s'ensuit, que les différentes propriétés
attachées aux applications en général peuvent se rencontrer avec les
mêmes définitions, dans l'étude des fonctions. Si
ce n'Ă©tait cet usage, qui peut avoir ses exceptions, les mots fonction
et application sont synonymes. Il s'ensuit, que les différentes propriétés
attachées aux applications en général peuvent se rencontrer avec les
mêmes définitions, dans l'étude des fonctions.
Une fonction de D dans
E (D et E Ă©tant donc des ensembles de nombres), est ainsi un objet
mathématique, que l'on peut noter f, et tel que quel que soit x
appartenant à D, il existe un élément unique y appartenant à E, tel
que y soit l'image de x par f (on dit aussi que y est la
valeur de f en x) :
f : 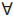 x x 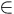 D, D, 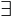 !
y !
y 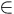 E | y = f(x) E | y = f(x)
x est appelée
la variable indépendante, y est la variable dépendante.
L'intérêt de cette
classe particulière d'applications que sont les fonctions est que certaines
propriétés des fonctions ou certaines opérations que l'on fait entre
les fonctions résultent des propriétés des nombres sur lesquels elles
agissent et sur les opérations possibles entre ces nombres. Ainsi les
propriétés des opérations telles que l'addition , la multiplication,
la dérivation ou l'intégration de fonctions, par exemple, sont-elles
directement attachées aux propriétés de l'ensemble 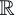 des nombres réels (ou, mieux dit, aux propriétés du corps commutatif
totalement ordonné (
des nombres réels (ou, mieux dit, aux propriétés du corps commutatif
totalement ordonné (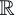 ,
+, ., ,
+, ., 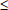 )). )).
Définitions générales
et notations.
Fonctions
réelles d'une variable réelle.
Dans ce qui suit
les diverses notions attachées aux fonctions seront introduites à partir
de l'étude de fonctions réelles d'une variable réelle (= fonctions
numériques) c'est-à -dire de fonctions f associant de façon
unique un nombre réel x à un autre
nombre réel y. Il existe
aussi des s fonctions impliquant davantage de variables ou des variables
qui ne sont pas exclusivement des nombres réels.
 Exemples
de fonctions qui ne sont pas des fonctions réelles d'une variable
réelle : une fonction telle que y = f(x1, x2,..,
xn) est une fonction de
n variables; une fonction
telle que y = f(x), lorsque x et y sont des nombres
complexes est une fonction complexe de variable complexe. Les
vecteurs ne sont pas des nombres, mais peuvent se définir à partir de
nombres (leurs coordonnées); on peut alors se trouver dans les situations
suivantes (entre autres) : lorsque l'argument x est un réel et l'image
y est un vecteur, la fonction telle que f(x) = y est une fonction vectorielle;
les champs scalaires se définissent comme des fonctions dont l'argument
est un vecteur et l'image un nombre (scalaire); dans le cas de champs vectoriels,
l'argument et l'image sont des vecteurs; etc. Exemples
de fonctions qui ne sont pas des fonctions réelles d'une variable
réelle : une fonction telle que y = f(x1, x2,..,
xn) est une fonction de
n variables; une fonction
telle que y = f(x), lorsque x et y sont des nombres
complexes est une fonction complexe de variable complexe. Les
vecteurs ne sont pas des nombres, mais peuvent se définir à partir de
nombres (leurs coordonnées); on peut alors se trouver dans les situations
suivantes (entre autres) : lorsque l'argument x est un réel et l'image
y est un vecteur, la fonction telle que f(x) = y est une fonction vectorielle;
les champs scalaires se définissent comme des fonctions dont l'argument
est un vecteur et l'image un nombre (scalaire); dans le cas de champs vectoriels,
l'argument et l'image sont des vecteurs; etc.
Une fonction réelle
à une variable réelle est une application dont le domaine de définition
(= ensemble de départ de la fonction) et l'ensemble image ( = ensemble
d'arrivée) sont des sous-ensembles de l'ensemble 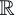 des nombres réels. Ces sous-ensembles (nécessairement non vides) pourront
ĂŞtre des intervalles de
des nombres réels. Ces sous-ensembles (nécessairement non vides) pourront
être des intervalles de 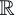 ou des réunions d'intervalles.
ou des réunions d'intervalles.
Si l'on note D (ou
Df) le sous-ensemble de 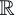 des éléments x sur lesquels agit la fonction f (autrement
dit si D est le domaine de définition de f), alors on appellera
ensemble
image de f le sous ensemble de
des éléments x sur lesquels agit la fonction f (autrement
dit si D est le domaine de définition de f), alors on appellera
ensemble
image de f le sous ensemble de 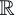 de toutes les images des éléments x de D par la fonction
f.
On le notera f(D), Im(f) ou Imf.
de toutes les images des éléments x de D par la fonction
f.
On le notera f(D), Im(f) ou Imf.
 Sauf
nécessité particulière, dans ce qui suit, on admettra, pour ne pas avoir
à se répéter, que lorsqu'on qu'on parle d'une fonction f, celle-ci
est définie sur un intervalle D auquel appartiennent les nombre réels
x, x0, x1, etc. Sauf
nécessité particulière, dans ce qui suit, on admettra, pour ne pas avoir
à se répéter, que lorsqu'on qu'on parle d'une fonction f, celle-ci
est définie sur un intervalle D auquel appartiennent les nombre réels
x, x0, x1, etc.
Graphe
d'une fonction. Représentation graphique.
Le sous-ensemble
{(x, f (x)) | x 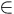 D} du produit cartésien D X f(D) est appelé le graphe de f.
Dans
le cas de beaucoup des fonctions réelles d'une ou plusieurs variables
réelles, on peut représenter un tel graphe sous la forme d'une courbe
(Ă©ventuellement avec plusieurs composantes disjointes) qui peut ĂŞtre
tracée sur le plan où l'abscisse est la valeur de la variable x
et l'ordonnée la valeur f(x). C'est ce qu''on appellera une représentation
graphique de la fonction, et l'on dira que la courbe a pour Ă©quation
y = f(x). Les éléments du graphe sont appelés points. Ils ont pour coordonnées
(x, f(x)).
D} du produit cartésien D X f(D) est appelé le graphe de f.
Dans
le cas de beaucoup des fonctions réelles d'une ou plusieurs variables
réelles, on peut représenter un tel graphe sous la forme d'une courbe
(Ă©ventuellement avec plusieurs composantes disjointes) qui peut ĂŞtre
tracée sur le plan où l'abscisse est la valeur de la variable x
et l'ordonnée la valeur f(x). C'est ce qu''on appellera une représentation
graphique de la fonction, et l'on dira que la courbe a pour Ă©quation
y = f(x). Les éléments du graphe sont appelés points. Ils ont pour coordonnées
(x, f(x)).
-
Figure
1 - Représentation graphique
d'une fonction.
Dfest
le domaine de définition de f;
Imf
est
l'ensemble image de f.
Quelques familles
de fonctions.
Fonctions
algébriques.
Les fonctions
algébriques sont des fonctions dans lesquelles les différents termes
(variables numériques) sont liés entre eux par par des symboles opératoires
(+, x, etc.) ou peuvent se ramener Ă des expressions n'utilisant que ces
symboles. Par exemple, la fonction f(x) = (x²+1)/(x-1) est une fonction
algébrique. Figurent parmi les fonctions algébriques :
• Les
fonctions polynomiales. - Ce sont des fonctions f telles que, pour
tout x du domaine de définition, f(x) = anxn
+ an - 1xn
- 1 + an - 2xn
-2 + ... + a1x + a0
, oĂą n un entier positif et les coefficients ai sont
des réels (ou des nombres complexes), avec an non
nul. Le nombre n indique le degré de la fonction polynomiale. Lorsque
n = 3 on parle de fonction cubique. La fonction f(x) = ax² + bx
+ c, (avec a 0), par exemple,
est une fonction du second degré. Sa courbe représentative est une parabole. 0), par exemple,
est une fonction du second degré. Sa courbe représentative est une parabole.
f(x) = ax²
+ bx + c peut aussi s'écrire : f(x) = a(x+b/2a)² - /4a,
oĂą /4a,
oĂą  -=
b²-4ac est appelé discriminant. Le mérite de cette forme du trinôme;
dite forme canonique, est de faire apparaître des termes d'un intérêt
particulier. Ainsi, le point de coordonnées (-b/2a, - -=
b²-4ac est appelé discriminant. Le mérite de cette forme du trinôme;
dite forme canonique, est de faire apparaître des termes d'un intérêt
particulier. Ainsi, le point de coordonnées (-b/2a, - /4a)
correspond-il au point oĂą la parabole (courbe de f) atteint son maximum
ou son minimum. Ces mĂŞmes coordonnĂ©es permettent aussi de dĂ©cider (Ă
partir d'une discussion sur le signe de /4a)
correspond-il au point oĂą la parabole (courbe de f) atteint son maximum
ou son minimum. Ces mĂŞmes coordonnĂ©es permettent aussi de dĂ©cider (Ă
partir d'une discussion sur le signe de  )
s'il existe ou pas des valeurs de x (appelées racines de l'équation)
telles que f(x) =0, et de les calculer Ă©ventuellement. )
s'il existe ou pas des valeurs de x (appelées racines de l'équation)
telles que f(x) =0, et de les calculer Ă©ventuellement.
Les fonctions
du second degré (aussi appelées trinômes du second degré), sont
un cas particulier (pour les fonctions d'une variable réelle) des fonctions
quadratiques qui sont des fonctions polynomiales de degré 2
Ă un nombre quelconque de variables (par ex., la fonction Ă deux variables
: f(x, y) = x² + 2xy).
Une fonction puissance
de degré n est une fonction polynomiale de la forme : f(x) = xn,
où x est un réel non nul et n un entier positif.
• Les fonctions
rationnelles. - Ce sont des fonctions polynomiales définies par une
relation de la forme f(x) = p(x) / q(x) (oĂą p et q sont des fonctions
polynomiales et oĂą au moins un des coefficients de q(x) est non nul).
• Les fonctions
irrationnelles. - Ce sont les fonctions qui font appel au symbole racine
:
n , avec n entier positif.
, avec n entier positif.
Fonctions
affines.
On appelle fonction
affine une fonction f telle que f(x) = ax + b (c'est donc
une fonction polynomiale de degré 1). La courbe représentative d'une
telle fonction est une droite : la constante a est son coefficient directeur
(= pente) et la constante b est son ordonnée à l'origine
(elle coupe l'axe des ordonnées au point (0, b)).
 On
remarquera que la somme de deux fonctions affines f et g (telles
que f(x) = ax+b et g(x) = a'x+b') est une fonction affine h (telle que
h(x)= (ax+b)+ (a'x+b') = (a+a')x+ b+b'), dont le coefficient directeur
est la somme des coefficients directeurs et dont l'ordonnée à l'origine
est la somme des ordonnées à l'origine. On
remarquera que la somme de deux fonctions affines f et g (telles
que f(x) = ax+b et g(x) = a'x+b') est une fonction affine h (telle que
h(x)= (ax+b)+ (a'x+b') = (a+a')x+ b+b'), dont le coefficient directeur
est la somme des coefficients directeurs et dont l'ordonnée à l'origine
est la somme des ordonnées à l'origine.
 De
même, la composée fog
de deux fonctions affines est aussi une fonction affine; elle est telle
que fog(x) = f(g(x))
= a(a'x+b') + b = aa'x+ab'+b. Et l'on notera au passage que fog
≠gof. De
même, la composée fog
de deux fonctions affines est aussi une fonction affine; elle est telle
que fog(x) = f(g(x))
= a(a'x+b') + b = aa'x+ab'+b. Et l'on notera au passage que fog
≠gof.
Lorsque a ou b sont
égaux à zéro ou quand a est égal à 1, on donne des noms particuliers
aux fonctions affines concernées :
• Dans
le cas ou a = 0 (f(x) = b), f est une fonction constante.
• Dans le cas ou
b = 0 (f(x) = ax), f est une homothétie ou fonction linéaire
de coefficient a.
• Dans le cas où
a = 1 et b = 0, f correspond Ă f(x) = x. C'est la fonction identique
(sur le domaine de définition D) : IdD.
• Dans le cas ou
a =1 et b 0, (f(x)
= x + b), f est une translation. 0, (f(x)
= x + b), f est une translation.
Les fonctions affines sont les fonctions les
plus simples, mais on verra plus bas qu'elles jouent un rĂ´le central dans
la définition de notions aussi fondamentales que celles de limite ou de
dérivée.
Fonctions
spéciales.
Les fonctions spéciales suivantes ont
plus ou moins de parentés avec les fonctions affines.
• Fonction
valeur absolue. - C'est la fonction, notée |x|, qui associe x à x
si x est supérieur ou égal à zéro (|x| = x) et à -x si x est inférieur
à zéro (|x| = -x).
• Fonction signe.
- C'est la fonction, notée sgn(x), qui associe à x les valeurs -1, 0
ou 1, selon le signe de x : sgn(x) =-1 si x < 0; sgn(x) = 0, si x =
0; sgn(x) = +1 si x > 0.
• Fonction en
escalier. - Une fonction f définie sur un intervalle fermé [a, b]
est appelée fonction en escalier (ou fonction constante par morceaux)
sur [a, b] s'il existe une subdivision S = (x0, ...,
xn) de [a, b] telle que f est constante sur chacun
des n intervalles ]x0, x1[,
... ]xn-1, xn[. On dit alors
aussi que f est étagée sur S . On donne le nom de
pas (ou
module)
de
la subdivision S, le plus grand des réels strictements positifs
x1-x0, ... , xn-1-
xn-1 (autrement dit, le pas ou module est la largeur
de la plus large marche de l'escalier). Ce nombre est aussi le pas de
la fonction f.
On fera appel plus
bas à la notion de fonction en escalier pour introduire celle d'intégrale
d'une fonction.
Fonctions
transcendantes.
Lorsqu'une fonction
numérique n'est pas algébrique on dit qu'elle est transcendante.
Exemples, les fonctions exponentielle, logarithmiques, circulaires, etc.
:
• Les
fonctions
exponentielles sont définies par une relation de la forme f(x)-=
ax, oĂą x, l'exposant, est
un réel, et a , appelée la
base, est un nombre réel strictement
positif différent de 1.
On appelle
exponentielle
naturelle la fonction exponentielle dont la base est le nombre irrationnel
e
= 2,718281828..., appelé nombre d'Euler ou constante
de NĂ©per.
• Les fonctions
logarithmiques sont des fonctions définies par une relation de la
forme f(x) = loga(x) oĂą a (base du logarithme)
est un réel strictement positif différent de 1. La fonction log10
se note aussi log.
On parle
de logarithme naturel quand la base est le nombre e mentionné
ci-dessus. On note cette fonction Log ou ln.
• Les fonctions
circulaires
(ou
trigonométriques)
sont des fonctions définies à partir des fonctions sinus et cosinus et
dont l'argument est une valeur d'angle, ou un angle de rotation. Parmi
les fonctions circulaires, on mentionnera, outre les fonctions sinus (sin)
et cosinus (cos), la fonction tangente (tg (x) = sin(x)/cos(x)), la fonction
sécante (sec(x) =
1/ cos (x)), etc.
• Ajoutons à cela
un certain nombre de fonctions apparentées aux fonctions circulaires
: les fonctions trigonométriques inverses (arcsin, arccos, arctan,
etc.); les fonctions hyperboliques (sinh, cosh, tanh, etc) et les
fonctions
hyperboliques inverses (argsinh, argcosh, etc.).
Quelques qualificatifs
pour les fonctions.
Fonctions
monotones.
Si l'on considère
deux éléments distincts quelconques x1 et x2
appartenant au domaine de définition de la fonction f, et tels
que x1 < x2, la fonction
est dite monotone si l'on a toujours soit f(x1) 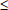 f(x2), soit f(x2)
f(x2), soit f(x2) 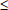 f (x1). Dans le premier cas la fonction est de plus
dite croissante, dans le second, elle est dite décroissante.
f (x1). Dans le premier cas la fonction est de plus
dite croissante, dans le second, elle est dite décroissante.
• Lorsque on a
f(x1) < f(x2) ou f(x2)
< f (x1), on dit que f est strictement monotone
(croissante ou décroissante).
• La propriété
de monotonie (croissante ou décroissante) peut ne s'observer que pour
un sous-ensemble du domaine de définition. Il convient alors de préciser
explicitement sur quel(s) intervalle(s) la fonction est monotone (croissante
ou décroissante) .
Fonctions
réciproques.
Comme toute autre application, une fonction
f bijective admet une fonction réciproque, notée f
-1
.
(Attention : ici, f-1
est le symbole d'une
fonction, pas une puissance de f; pour Ă©viter les confusions on peut aussi
noter f* la réciproque de f)). Pour trouver la fonction réciproque de
f, les variables x et y sont interverties dans la formule de f, puis y
est exprimé à partir de x = f (x) afin d'obtenir y = f-1(x).
L'expression y = f (x) est Ă©quivalente Ă l'expression x =
f-1(y).
Les égalités suivantes
découlent de cette relation :
f (f-1
(y)) = y et f-1(f (x)) = x
Autre Ă©criture :
(f o
f-1)(y)
= y et (f-1o f) (x)
= x
Le graphe d'une fonction
réciproque y = f-1 (x) est obtenu
par réflexion du graphe de y = f (x) par rapport à la droite y = x.
• Si une
fonction f est strictement monotone dans un intervalle de son domaine de
définition, alors il existe une fonction réciproque f-1
pour cet intervalle.
• Si une fonction
non monotone peut être partitionnée en parties strictement monotones,
alors la réciproque correspondante existe pour chaque partie.
Fonctions
bornées.
Une fonction est
dite bornée s'il existe une valeur b qu'elle prend, telle que quelque
soit x, f(x) est toujours soit inférieur ou égal à b, soit supérieur
ou égal à b. Dans le premier cas, b est la borne supérieure de la fonction,
dans le second, b est sa borne inférieure.
Fonctions
paires et impaires.
Une fonction
paire est une fonction telle que f(x) = f(-x). Une fonction impaire
est une fonction telle que f(x) = -f(-x).
• Sous
réserve que, pour tout x appartenant au domaine de définition D de la
fonction f, -x appartiennent aussi Ă D, la fonction f
peut ĂŞtre Ă©crite comme la somme d'une fonction paire g et d'une
fonction impaire h. On a ainsi, pour chaque x appartenant au domaine
de définition de f :
f(x) = g(x)
+ h(x), où g(x) = ½.[f(x) + f(-x)] et h(x) = ½.[f(x) - f(-x)].
Fonctions
périodiques.
Une fonction est
périodique
si elle satisfait la relation f(x) = f(x+T), oĂą T est une constante non
nulle. De cette définition, il suit que la relation f(x) = f(x+n.T), où
n est entier relatif non nul, est aussi vérifiée. T, plus petit nombre
positif vérifiant ces relations, est appelée la période de la
fonction.
Limites et continuité
Limite d'une fonction.
On appelle limite d'une quantité
variable une quantité fixe dont cette variable s'approche indéfiniment,
de manière à en différer d'aussi peu que l'on veut. La considération
de cette notion de limite intervient constamment dans l'Ă©tude des fonctions.
Limite
d'une fonction en un point.
Parler de la limite d'une fonction
réelle en un point revient à se demander ce qu'il advient de la valeur
f(x)
d'une
fonction f lorsque la variable x tend vers une valeur x0donnée.
Pour une variable réelle quelconque
x,
tendre vers une valeur donnée x0 signifie
que la valeur absolue 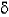 de la différence de x et de x0 (
de la différence de x et de x0 (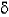 =| x- x0 |) tend vers zéro. On écrit cette
situation : x
=| x- x0 |) tend vers zéro. On écrit cette
situation : x  x0 (lire : "x tend vers x0"),
ou de manière équivalente
x0 (lire : "x tend vers x0"),
ou de manière équivalente 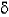  0.
0.
La limite de la valeur de la fonction f
quand x tend vers x0, se notera alors-:
lim f(x)
ou, de manière plus économique :
x  x0
x0 |
lim f , voire : lim f
x0 |
Cette limite peut ĂŞtre
un nombre, quand f(x) tend vers une valeur butoir; mais elle peut aussi
être infinie (± )
quand la valeur absolue de f(x) tend indéfiniment vers + )
quand la valeur absolue de f(x) tend indéfiniment vers + ou vers -
ou vers - . .
Limite
finie en un point.
Admettons, pour commencer, que cette limite
soit un nombre (on parlera dans ce cas de limite finie), et que
ce nombre soit noté A. La définition de la limite est alors :
lim f(x) = A 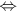 [
[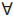  > 0,
> 0, 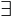 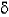 > 0 / | x-x0| <
> 0 / | x-x0| < 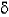 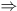 |f(x)-A| <
|f(x)-A| <  ] ]
x  x0
x0
La limite d'une fonction en un point peut
ĂŞtre la valeur de la fonction en ce point ou ĂŞtre distincte de cette
valeur.
Limite
Ă droite et limite Ă gauche.
On a admis implicitement jusqu'ici qu'un
fonction a une mĂŞme limite en x0 que l'on approche
x0 par des valeurs de x supérieures à x0
ou par des valeurs inférieures. Mais il peut arriver que les limites soit
différentes selon que l'on approche x0 par par des
valeurs de x supérieures (limite à droite) ou par par des valeurs de
x inférieurs (limite à gauche). On écrit : x  x0+ lorsque x > x0,
et l'on Ă©crit x
x0+ lorsque x > x0,
et l'on Ă©crit x  x0- lorsque x < x0.
D'oĂą les deux notations suivantes :
x0- lorsque x < x0.
D'oĂą les deux notations suivantes :
• Limite à droite : lim
f(x) = P
x  x0+
x0+
• Limite à gauche : lim f(x) =
M
x  x0-
x0-
Où P et M sont des nombres réels.
On dit que la fonction f a une limite
en x0 si et seulement P et M existent et P
= M, dans le cas contraire, on devra toujours préciser "à droite" ou
"Ă gauche".
Limite
finie d'une fonction quand x tend vers l'infini.
On peut ĂŞtre conduit
Ă s'interroger sur ce que devient une fonction, non plus seulement quand
la variable x tend vers une valeur finie (x  x0), mais aussi quand cette variable tend vers ±
x0), mais aussi quand cette variable tend vers ± (x
(x  ± ± ).
Les notations ).
Les notations
a) lim
f(x) = A et b)
lim f(x) = A
x  + + x
x  -
-
signifient :
a)si
pour tout réel positif donné  il existe un nombre N > 0 tel que pour tout x > N, la valeur correspondante
f (x) est dans l'intervalle a-
il existe un nombre N > 0 tel que pour tout x > N, la valeur correspondante
f (x) est dans l'intervalle a- < f (x) < A +
< f (x) < A +  ; ;
b) et, de
façon analogue, que A est la limite de la fonction f (x) quand x tend
vers - si
pour tout nombre positif donné si
pour tout nombre positif donné  il existe un nombre positif N > 0 tel que pour tout x < -N la valeur
correspondante f(x) appartient Ă l'intervalle a-
il existe un nombre positif N > 0 tel que pour tout x < -N la valeur
correspondante f(x) appartient Ă l'intervalle a- < f (x) < A +
< f (x) < A +  . .
Propriétés
des limites.
• Toute quantité croissante
(ou décroissante) qui ne peut devenir plus grande (ou plus petite) qu'une
quantité donnée fixe, a une limite.
• Si f(x) = k, 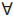 x
x 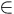 [a, b] [a, b]  lim f(x) = k, x0
lim f(x) = k, x0 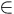 [a, b]
[a, b]
x x0
x0
• La limite d'une somme (ou d'un produit)
de quantités variables en nombre déterminé est égale à la somme (ou
au produit) des limites de ces quantités. La limite d'un quotient est
Ă©gale au quotient des limites du dividende et du diviseur (si le diviseur
est différent de zéro).
Si lim f(x) = A et lim g(x) = B,
on vérifie que
x  x0 x
x0 x  x0
x0
a)
lim [f(x)±g(x)] = A±B
x  x0
x0
b)
lim [f(x).g(x)] = A.B
x  x0
x0
c)
si B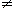 0,
lim [f(x)/g(x)] = A/B 0,
lim [f(x)/g(x)] = A/B
x  x0
x0
d)
lim k.f(x) = k.A
x  x0
x0
Limites
infinies.
On a admis jusqu'ici
que la limite d'une fonction en un point était un nombre réel. Mais ce
n'est pas toujours le cas. Il peut arriver que, lorsque x s'approche idéfiniment
de x0, la valeur absolue de f(x) croisse indéfiniment.
Lorsqu'une valeur tend ainsi à devenir indéfiniment grande, on dit qu'elle
tend vers "plus l'infini" ou vers "moins l'infini". Ces situations se notent
:
lim f(x)
= +
x  x0
x0
lim f(x) = -
x  x0
x0
Elles signifient que  M > 0,
M > 0,   , ,  fonction de M/f(x) > M (ou < -M, dans le second cas) tant que
|x < x0| <
fonction de M/f(x) > M (ou < -M, dans le second cas) tant que
|x < x0| <  . .
 Note
: on peut aussi se trouver dans des situations telles que, par exemple
: Note
: on peut aussi se trouver dans des situations telles que, par exemple
:
lim f(x)
= - ,
lim f(x) = k , etc. ,
lim f(x) = k , etc.
x  +
+ x
x  -
-
(Tous les cas de
figure sont possibles).
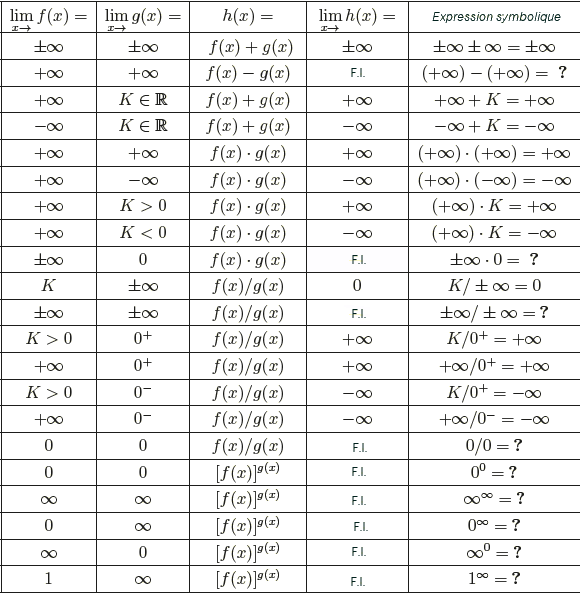
Formes
indéterminées.
Les propriétés
(somme, produit, rapport) des limites infinies sont analogues Ă celles
des limites finies tant qu'on ne se trouve pas dans les cas oĂą apparaissent
certaines expressions, appelées formes indéterminées (F. I.)
Ainsi, notamment, on ne peut pas conclure
directement Ă l'existence de :
• lim (f+g), lorsque lim f =
+ et lim g = - et lim g = - .
(indétermination .
(indétermination  - - ) )
• lim f.g, lorsque lim f = 0 et lim g
= ± . (indétermination
0x . (indétermination
0x ) )
• lim f/g, lorsque lim f = ± et lim g = ±
et lim g = ± (indétermination
(indétermination / / )
. )
.
Donner la limite dans
ces situations s'appelle lever l'indétermination. Ce n'est pas
toujours possible.
 Typiquement,
l'impossibilité de lever algébriquement l'indétermination intervient
quand on travaille sur des fonctions transcendantes ou sur des fonctions
mêlant fonctions transcendantes et fonctions algébriques. Ainsi, par
exemple, la limite quand x tend vers zéro de (e²x
-
1)/x aboutit-elle à l'indétermination 0/0. On peut alors tenter, de résoudre
le problème de manière algébrique en réécrivant l'expression et en
cherchant la limite quand x tend vers zéro de (e²x/x)
- (1/x). Mais cela conduit à une autre forme indéterminée ( Typiquement,
l'impossibilité de lever algébriquement l'indétermination intervient
quand on travaille sur des fonctions transcendantes ou sur des fonctions
mêlant fonctions transcendantes et fonctions algébriques. Ainsi, par
exemple, la limite quand x tend vers zéro de (e²x
-
1)/x aboutit-elle à l'indétermination 0/0. On peut alors tenter, de résoudre
le problème de manière algébrique en réécrivant l'expression et en
cherchant la limite quand x tend vers zéro de (e²x/x)
- (1/x). Mais cela conduit à une autre forme indéterminée ( - - ). ).
On verra plus bas, après
avoir étudié la notion de dérivée d'une fonction, comment il peut être
possible de sortir d'une telle impasse ( règle
de L'Hôpital). règle
de L'HĂ´pital).
-
Limites
infinies et formes indéterminées
Infinitésimaux.
Le terme d'infinitésimal
s'applique à toute quantité variable qui tend vers 0 (c'est-à -dire aussi
petite que l'on veut, sans jamais ĂŞtre Ă©gale Ă 0). On appelle fonction
infinitésimale au point x0 toute fonction  telle que
telle que
lim (x)
= 0 (x)
= 0
x  x0
x0
On est dans une situation similaire lorsqu'on
a  (x)
qui tend vers zéro quand x tend vers un infini : (x)
qui tend vers zéro quand x tend vers un infini :
lim  (x)
= 0 (x)
= 0
x  ± ±
La fonction  peut être une fonction très banale :par exemple la fonction sinus
ou la fonction identique au point x=0, ou encore la fonction 1/x quand
x tend vers l'infini, etc.
peut être une fonction très banale :par exemple la fonction sinus
ou la fonction identique au point x=0, ou encore la fonction 1/x quand
x tend vers l'infini, etc.
On peut comparer les infinitésimaux entre
eux.
• Deux infinitésimaux,  (x)
et (x)
et 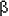 (x)
sont dits comparables lorsque (x)
sont dits comparables lorsque
lim 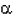 (x)
/ (x)
/ 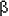 (x)
= A, et A est un nombre déterminé. (x)
= A, et A est un nombre déterminé.
x  x0 x0
C'est à cette possibilité de comparaison
que renvoie la notion d'ordre d'un infinitésimal.
• Lorsque A = 0, 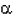 (x)
est d'ordre supérieur à (x)
est d'ordre supérieur à 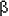 (x). (x).
• Lorsque A 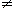 0
(et A 0
(et A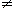 ± ± ), ), 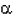 (x)
et (x)
et 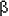 (x)
sont du mĂŞme ordre. (x)
sont du mĂŞme ordre.
• Lorsque A = ± , , 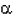 (x)
est d'ordre inférieur à (x)
est d'ordre inférieur à 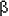 (x). (x).
• Lorsque A = 1, 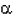 (x)
et (x)
et 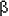 (x)
sont Ă©quivalents. (x)
sont Ă©quivalents.
Les infinitésimaux sont l'un des moyens utilisables
pour lever les formes indéterminées de type 0/0.
Continuité d'une
fonction.
Fonction
continue en un point.
Une fonction réelle f d'une variable
réelle est continue en x0 si et seulement
si sa limite en x0 est la valeur de la fonction en
ce point :
lim f(x)
= f(x0)
x  x0
x0
Cela signifie que, dans le cas d'une fonction
f continue en x0, les valeurs que prend cette fonction
pour des points proches de x0 doivent aussi ĂŞtre
proches de f(x0).
De la même façon que les limites d'une
fonction en un point x0 peuvent ĂŞtre dĂ©finies Ă
droite (x > x0) ou Ă gauche (x < x0),
il est possible aussi qu'une fonction ne soit continue qu'Ă droite ou
Ă gauche.
• Continuité à droite,
si et seulement si lim f(x) = f(x0)
x  x0+
x0+
• Continuité à gauche, si et
seulement si lim f(x) = f(x0)
x  x0-
x0-
Fonction
continue sur un intervalle.
Une fonction f est
continue sur l'intervalle ouvert ]a, b[ si elle est continue en chaque
point de cet intervalle.
Une fonction f est
continue sur l'intervalle fermé [a, b] si elle est continue si :
1)
f est continue sur l'intervalle ouvert ]a, b[;
2)
lim f(a) = a et lim f(b) = f(b).
Continuité
uniforme.
Une fonction f est
dite uniformément continue sur l'intervalle I = [a, b] si sur cet intervalle:
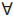  > 0,
> 0, 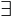 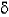 > 0 tel que pour tout couple x1, x2
d'éléments appartenant à I et vérifiant |x1---x2|
<
> 0 tel que pour tout couple x1, x2
d'éléments appartenant à I et vérifiant |x1---x2|
< 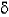 ,
on
ait |f(x1) - f(x2)| < ,
on
ait |f(x1) - f(x2)| < .
Le nombre .
Le nombre 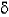 associĂ© Ă
associé à  ne dépend pas ici de x, alors que dans la définition de la continuité
tout court il peut en dépendre.
ne dépend pas ici de x, alors que dans la définition de la continuité
tout court il peut en dépendre.
La continuité uniforme
implique la continuité tout court, mais la réciproque est fausse.
Prolongement
par continuité.
On considère un
intervalle I auquel appartient le réel a et la fonction f définie
sur I-{a} (c'est-Ă -dire sur l'intervalle
I auquel
on a ôté le nombre a). Si f est continue sur cet intervalle et
a une limite finie A en a, alors la fonction Ć' dĂ©finie
sur I et telle que, pour tout x de I-{a}, on
ait Ć'(x) = f(x) et Ć'(a) = A, est continue en
a et sur I.
On appelle alors Ć' le prolongement par continuitĂ© de f en a.
Propriétés
locales des fonctions continues.
On peut attacher
aux fonctions continues les propriété suivantes :
• La somme
de deux fonctions continues est une fonction continue.
• Le produit de
deux fonctions continues est une autre fonction continue.
• Le quotient de
deux fonctions continues est une fonction continue en
tout point ou sur
tout intervalle dans lequel le dénominateur ne s'annule pas.
• Si f est continue
en a, f (a) = b et g est continue en b, alors la composée
gof (c'est-Ă -dire la fonction telle que g(f (x)))
est continue en a.
• Théorème de
Weierstrass. - Si f est continue sur un intervalle fermé [a, b], elle
est bornée sur cet intervalle. De plus, si S est l'ensemble des valeurs
f (x) pour x appartenant Ă [a, b], et M = sup S, il existe un point 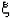 appartenant Ă [a, b] tel que f (
appartenant Ă [a, b] tel que f (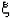 )
= M et donc idem pour m = inf S). On dit alors qu'une fonction continue
dans un intervalle compact (= fermé et borné) [a, b] y atteint un maximum
et un minimum. )
= M et donc idem pour m = inf S). On dit alors qu'une fonction continue
dans un intervalle compact (= fermé et borné) [a, b] y atteint un maximum
et un minimum.
Calcul différentiel
Différentielles
et dérivées.
Approche
géométrique.
On peut donner un sens géométrique aux
notions de différentielle et de dérivée en considérant :
1) le graphe d'une fonction f,
c'est-Ă -dire la courbe C d'Ă©quation y = f(x). On admet que f est continue
dans le voisinage de x0, c'est-Ă -dire sur
un intervalle V centré sur un point x0, tel que V
= ]x0 - 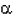 , x0 +
, x0 + 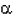 [, [,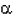 étant un réel strictement positif.
étant un réel strictement positif.
2) Deux points distincts de cette courbe
P et Q de coordonnées respectives (x0, f(x0))
et (x, f(x)), oĂą x0 et x appartiennent Ă l'intervalle
V. Si l'on note h la différence de x et X0 (h =x-x0)
les coordonnées de Q pourront aussi s'écrire : (x0+h,
f(x0+h), oĂą |h| < 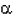 ,
et (puisque les points sont distincts) h ,
et (puisque les points sont distincts) h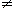 0. 0.
3) Une droite D est sécante de la courbe
C au point P et au point Q de coordonnées (x = x0
+
h, y = f(x0 + h)), avec h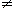 0.
Sa pente m peut s'Ă©crire-: m = [f(x0
+
h) - f(x0)]/h. 0.
Sa pente m peut s'Ă©crire-: m = [f(x0
+
h) - f(x0)]/h.
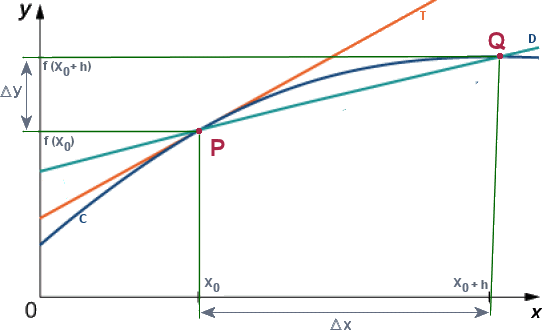
Figure
2. - SĂ©cante et tangente en un point
d'une
courbe représentative d'un fonction continue.
La question est maintenant de savoir ce
que devient cette pente lorsque Q se rapproche autant que l'on veut de
P, autrement dit quand x se rapproche aussi près que l'on veut de x0,
ou encore lorsque h tend vers 0 (h 0). Dans notre exemple, il existe une réponse : la droite D tend à se
confondre avec la tangente de la courbe C au point P. Et l'on peut exprimer
cela de deux façons équivalentes :
0). Dans notre exemple, il existe une réponse : la droite D tend à se
confondre avec la tangente de la courbe C au point P. Et l'on peut exprimer
cela de deux façons équivalentes :
1) Au voisinage de x0,
la droite D et la courbe C tendent Ă se confondre, autrement dit, si plus
une portion de C au voisinage de x0 est petite et plus elle s'approche
d'une segment de droite : la fonction f peut donc être approchée
autant qu'on le souhaite par une fonction affine. Cela renvoie Ă la notion
de différentiabilité.
2) lorsque h tend vers zéro, la
pente de D tend vers une limite finie, qui est aussi la pente de la tangente
en x0. Cette condition renvoie à la notion de dérivabilité.
Dans le cas des fonctions réelles à une
variable différentiabilité et dérivabilité coïncident : une fonction
différentiable (en un point) est dérivable (en ce point) et réciproquement.
Cette équivalence est utile pour choisir sous quel angle on résoudra
tel ou tel problème : l'un sera plus simple à aborder en termes de différentielles,
l'autre en termes de dérivées.
Différentiabilité.
Différentielle.
La fonction f est différentiable
en x0 si les conditions suivantes sont remplies :
a)
Il existe un intervalle V = ]x0 -  ,
x0 + ,
x0 + 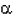 [
(on dit : "un intervalle V centré sur x0 et de rayon [
(on dit : "un intervalle V centré sur x0 et de rayon 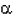 ")
inclus dans le domaine de définition D, b)
il existe un réel m; c) il existe fonction ")
inclus dans le domaine de définition D, b)
il existe un réel m; c) il existe fonction  définie sur V, qui a la propriété de tendre vers zéro quand x tend
vers x0 (autrement dit :
définie sur V, qui a la propriété de tendre vers zéro quand x tend
vers x0 (autrement dit :  est un infinitésimal); tels que d)
est un infinitésimal); tels que d)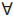 x
x 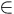 V, f(x) = f(x0)
+ m.(x-x0) + (x-x0). V, f(x) = f(x0)
+ m.(x-x0) + (x-x0). (x). (x).
On peut alors définir les fonctions suivante
:
•
La fonction affine tangente Ă f au point x0
est la fonction qui Ă tout x de D associe m.x + f(x0)
- m.x0
• La différentielle
de f en x0 (ou fonction linĂ©aire tangente Ă
f au point x0) est la fonction qui Ă tout
x de D associe mx, et que l'on note dfx0;
m étant le coefficient de la différentielle f en x0.
Propriétés
des fonctions différentiables.
On considère des réels k, x, x0,
et deux fonctions réelles, f et g, définies sur un voisinage V de
x0 et différentiables en x0.
On a alors :
• f +
g est différentiable au point x0 et d(f+g)x0
= dfx0 + dgx0
• k.f est différentiable
au point x0 et d(k.f)x0
= k.dfx0
• f.g est différentiable
au point x0 et d(fg)x0
= f(x0).dgx0
+ g(x0).dfx0
• Si g(x)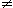 0 pour tout x appartenant à V, f/g est différentiable au point x0 et
:
0 pour tout x appartenant à V, f/g est différentiable au point x0 et
:
d(f/g)x0
= [g(x0)dfxx0 - f(x0)dgx0]/g²(x0)
• Si f est différentiable
sur un voisinage V de x0 et g est différentiable
sur un voisinage W de f(x0), (avec f(V) 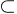 W) alors la fonction composée g o f est différentiable
au point x0 et on a : d(g o f)x0
= dg f(x0) o dfx0
W) alors la fonction composée g o f est différentiable
au point x0 et on a : d(g o f)x0
= dg f(x0) o dfx0
Dérivabilité.
Nombre dérivé en un point. Fonction dérivée.
Si la limite du rapport f(x) - f(x0)
/ x - x0, quand x tend vers x0,
existe et est finie, on dit que f est dérivable en x0,
 = lim [f(x) - f(x0)]/(x
- x0)
= lim [f(x) - f(x0)]/(x
- x0)
x  x0
x0
 est appelé le nombre dérivé de f en x0.
C'est
le taux de variation de f en ce point, ou encore la pente de la tangente
à la courbe représentative de f au point de coordonnées
[x0, f(x0)].
est appelé le nombre dérivé de f en x0.
C'est
le taux de variation de f en ce point, ou encore la pente de la tangente
à la courbe représentative de f au point de coordonnées
[x0, f(x0)].
 Dire
que "f est dérivable en x0 et de nombre dérivé Dire
que "f est dérivable en x0 et de nombre dérivé  "
est équivalent à dire que " f est est différentiable en x0
et le coefficient de sa différentielle est "
est équivalent à dire que " f est est différentiable en x0
et le coefficient de sa différentielle est  ". ".
On appelle fonction dérivée de f
(ou plus simplement dérivée de f) la fonction , ordinairement
notée f' (lire "f prime"), qui, à tout x appartenant à un intervalle
I (non vide et inclus dans le domaine de définition de f) associe le nombre
dérivé de f en x.
 Toute
fonction dérivable (différentiable) en un point est continue en ce point.
Mais la réciproque est fausse. Toute
fonction dérivable (différentiable) en un point est continue en ce point.
Mais la réciproque est fausse.
DĂ©rivation
Ă droite et Ă gauche.
De la même façon que l'on a défini
plus haut une limite à droite et une limite à gauche, on peut définir
les notions de dérivabilité à droite et une dérivabilité à gauche
:
• Une fonction f définie sur
[x0, x0+r,
avec r >0 [ (resp. sur ]x0-r, x0])
est dérivable à droite (resp. à gauche) si et seulement
si la fonction qui associe Ă x la valeur f(x)-f(x0)/x-x0
a une limite finie Ă droite (resp. Ă gauche).
• Une fonction est dérivable seulement
si elle a une dérivée à droite, une dérivée à gauche et que ces dérivées
coincident en chaque point.
Les dérivées d'une fonction peuvent exister
à droite et à gauche d'un point, mais être différentes :
 Exemple
: Considérons la fonction valeur absolue : f(x) = |x|, qui est continue
sur Exemple
: Considérons la fonction valeur absolue : f(x) = |x|, qui est continue
sur 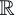 ; pour toutes
les valeurs de x supérieures à 0 (tous les points à droite de zéro),
la dĂ©rivĂ©e est f'(x) = 1, mais pour toutes les valeurs infĂ©rieures Ă
0 (tous les points Ă gauche de 0), elle est f'(x) = -1. Il n'y a donc
pas une limite unique selon que l'on considère x ; pour toutes
les valeurs de x supérieures à 0 (tous les points à droite de zéro),
la dĂ©rivĂ©e est f'(x) = 1, mais pour toutes les valeurs infĂ©rieures Ă
0 (tous les points Ă gauche de 0), elle est f'(x) = -1. Il n'y a donc
pas une limite unique selon que l'on considère x  0+ et x
0+ et x  0-. Bien que f(x) soit continue en 0, qu'elle soit dérivable
à droite de 0 et à gauche de 0, elle n'est pas dérivable en 0.
0-. Bien que f(x) soit continue en 0, qu'elle soit dérivable
à droite de 0 et à gauche de 0, elle n'est pas dérivable en 0.
On peut aussi se trouver
dans le cas où une fonction continue est dérivable en un point d'un côté
et pas de l'autre. Et, bien sûr, certaines fonctions peuvent n'être dérivables
ni à gauche ni à droite d'un point donné. Il existe même des fonctions
continues sur tout leur domaine de définition (qui peut être 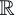 tout entier), mais qui ne sont dérivables nulle part. Karl
Weierstrass s'était fait une spécialité de la recherche de telles
fonctions : la première découverte, en 1872, porte le nom de fonction
de Weierstrass-Hardy. Sa représentation graphique est typiquement
ce que les mathématiciens appellent une
fractale : lorsqu'on zoome
sur un fragment de courbe (irrégulier dès le départ), le même motif
irrégulier apparaît, même chose lorsqu'on zoome encore et encore...
jusqu'Ă l'infiniment petit (
tout entier), mais qui ne sont dérivables nulle part. Karl
Weierstrass s'était fait une spécialité de la recherche de telles
fonctions : la première découverte, en 1872, porte le nom de fonction
de Weierstrass-Hardy. Sa représentation graphique est typiquement
ce que les mathématiciens appellent une
fractale : lorsqu'on zoome
sur un fragment de courbe (irrégulier dès le départ), le même motif
irrégulier apparaît, même chose lorsqu'on zoome encore et encore...
jusqu'Ă l'infiniment petit ( La
Géométrie fractale). La
Géométrie fractale).
Dérivées
successives.
Lorsqu'une fonction
f est dérivable, sa dérivée peut être (ou ne pas être) elle-même
dérivable. Si elle est dérivable, il sera possible de définir une dérivée
de la dérivée, qui sera appelée la dérivée seconde de f (la
dérivée tout court étant sa dérivée première). La dérivée de la
dérivée seconde, si elle existe, s'appellera la dérivée troisième
ou dérivée d'ordre 3, etc. Tant que la dérivabilité des dérivées
successives sera assurée, on parlera de dérivées d'ordre n de
f. On les Ă©crira f(n). Si pour tout entier
n strictement positif f est n fois dérivable, on dira que f est indéfiniment
dérivable.
Notations
de Lagrange, de Leibniz et de Newton.
• Notation
de Lagrange. - C'est la notation,
employée jusqu'ici pour les dérivées : elle utilise le signe ' (prime)
ou, pour les dérivées d'ordre n, l'exposant entre parenthèses
(n).
• Notation de
Leibniz. - Avec cette notation, dite aussi notation différentielle
de la dérivée, la dérivée d'une fonction f s'écrit df/dx . Si
l'on pose y = f(x), on pourra aussi l'Ă©crire dy/dx.
La notation de Leibniz
est souvent utilisée conjointement à celle de Lagrange. Exemples :
 On
peut écrire : f'(x) = dfx/dx, ou de façon équivalente
(rencontrée dans le formalisme du calcul
intégral) : On
peut écrire : f'(x) = dfx/dx, ou de façon équivalente
(rencontrée dans le formalisme du calcul
intégral) :
dfx
= f'(x).dx.
 A
partir de l'expression de la composée de deux fonctions différentiables
f et g (avec les mêmes conditions que celle mentionnées plus haut), peut
s'Ă©crire : A
partir de l'expression de la composée de deux fonctions différentiables
f et g (avec les mêmes conditions que celle mentionnées plus haut), peut
s'Ă©crire :
d(g o
f)x /dx= = g'(f(x)). f'(x) = dg
f(x) / dfx. dfx/dx
En posant y = f(x) et
z = g(x), l'expression de la dérivée de g o f prend
une forme intéressante :
dz/dx =
dz/dy.dy/dx
Ajoutons que, dans la
notation de Leibniz, la dérivée seconde se note d²y/dx² et la dérivée
nème : dny/dxn.
Il s'agit lĂ d'une convention d'Ă©criture et non pas d'un vrai quotient
comme dans le cas de la dérivée première.
• Notation de
Newton. - On rencontre aussi parfois en physique (principalement en
dynamique) la notation de Newton, qui Ă©crit la
dérivée sous la forme d'une lettre surmontée d'un point-: 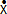 = f'(x). La dérivée seconde se note en surmontant la lettre de
deux points :
= f'(x). La dérivée seconde se note en surmontant la lettre de
deux points :  .
Selon ces conventions, la vitesse (dérivée de l'abscisse d'un mobile
variant dans le temps) s'Ă©crira : v = .
Selon ces conventions, la vitesse (dérivée de l'abscisse d'un mobile
variant dans le temps) s'Ă©crira : v = 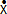 ,
et l'accélération (dérivée de la vitesse par rapport au temps) : a
= ,
et l'accélération (dérivée de la vitesse par rapport au temps) : a
=  = =  . .
Fonctions
de classe C1.
Pour mémoire, notons
qu'on dit qu'une fonction numérique f d'une variable réelle définie
sur un intervalle donné est de classe C1
si elle est dérivable sur cet intervalle et si sa dérivée f' est continue
sur cet intervalle. Cette propriĂ©tĂ© est une condition nĂ©cessaire Ă
l'établissement de certains résultats du calcul intégral.
Extrémums
absolus et relatifs.
Le maximum absolu Ma
(respectivement minimum absolu ma) d'une fonction
sur son domaine de définition D, c'est-à -dire la valeur maximale (resp.
minimale) prise par f(x) pour tout x appartenant Ă D, est telle que f(x)
est toujours inférieur (resp. supérieur) ou égal à Ma
et il existe un élément c de D tel que Ma = f(c).
Les extrémums (ou extrema si vous parlez latin) relatifs
(maximum relatif Mr et minimum relatif
mr) répondent à une définition analogue, si ce
n'est qu'ici on ne consière plus domaine de définition D dans sa totalité,
mais un sous-ensemble de D.
• [Ma
(resp. ma) est un maximum (resp. minimum) absolu de
f sur D] 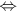 [ [ x x D,
f(x) D,
f(x)  Ma
(resp. f(x) Ma
(resp. f(x) ma)
et ma)
et  c c 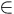 D
/ Ma (resp. ma) = f(c)] D
/ Ma (resp. ma) = f(c)]
• [Mr(resp.
mr) est un maximum (resp. minimum) relatif de f] 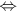 [
[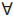 x x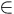 E(x1) E(x1) D,
f(x) D,
f(x) 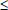 Mr (resp. f(x) Mr (resp. f(x) 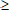 mr) et Mr (resp. mr)
= f(x1)]
mr) et Mr (resp. mr)
= f(x1)]
Bien sûr le sous-ensemble considéré peut
être égal à D lui-même, si bien que les extrémums absolus ne sont,
au final qu'un cas particulier des extrémums relatifs.
Une manière de considérer
un extrémum consiste à examiner comment se comporte la fonction f (définie
sur un intervalle [a, b]) dans le voisinage de cet extrémum : si elle
est croissante à sa gauche et décroissante à sa droite, on a affaire
Ă un maximum; si elle est dĂ©croissante Ă sa gauche et croissante Ă
sa droite, on a affaire à un minimum. Dans les deux cas, l'extrémum définit
le point pour lequel la fonction ne croît ni ne décroît, ce qui signifie
que; si elle existe, sa dérivée y est nulle.
• [f(x0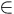 [a, b] est un extrémum et f'(x0) existe]
[a, b] est un extrémum et f'(x0) existe] 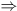 f'(x0) = 0
f'(x0) = 0
Points
d'inflexion.
Dans la représentation
graphique d'une fonction, les extrémums correspondent aux points de rebroussement
de la courbe. Lorsqu'on s'approche de ce point de rebroussement la pente
de la courbe diminue pour finir par s'annuler complètement (c'est ce que
signifie l'annulation de la dérivée).
Voyons maintenant
ce qui se passe, sur la portion de la courbe reliant deux extrémums consécutifs.
Lorsque x s'éloigne du premier extrémum, la pente, initialement nulle,
de la courbe augmente, pour diminuer lorsque ensuite Ă l'approche du second
extrémum. Dit autrement, la dérivée qui avait une valeur nulle atteint
ensuite maximale (ou minimale) puis se rapproche de nouveau de zéro, pour
l'atteindre arrivée à l'extrémum. Dans l'intervalle, la dérivée a
donc aussi eu un extrémum, qui est défini par le point ou la dérivée
de la dérivée est nulle, c'est-à -dire au point M0
où la dérivée seconde de la fonction f s'annule (f"(x0)
= 0) et change de signe. On appelle M0, un point
d'inflexion.
En termes plus mathématiques,
on aura la définition suivante : Si f est une fonction deux fois dérivable
sur un intervalle I de centre x0 et si la fonction
dérivée seconde f" s'annule en x0
en changeant de
signe, alors le point M0, de coordonnées (x0,f(x0))
est un point d'inflexion.
Dérivées
partielles.
On n'a parlé jusqu'ici
que de des dérivées des fonction réelles d'une variable réelle. Mais
la notion de dérivée (comme celle de différentielle) peut aussi s'appliquer
Ă des fonctions de plusieurs variables, telles, par exemple, que f : (x,
y, z, ...) u. On pourra alors définir autant de dérivées que de variables, appelées
alors dérivées partielles. Chacune d'elle correspondant au taux de variation
de la fonction quand un seul de ses arguments varie.
u. On pourra alors définir autant de dérivées que de variables, appelées
alors dérivées partielles. Chacune d'elle correspondant au taux de variation
de la fonction quand un seul de ses arguments varie.
Asymptotes.
Un asymptote
est une droite dont se rapproche indéfiniment une courbe (autrement dit
une droite tangente d'une courbe Ă l'infini).
• Asymptote
oblique. - La droite d'Ă©quation y = ax+b est asymptote Ă la courbe de
la fonction f(x) si la différence f(x) - y tend vers zéro quand x tend
vers (plus ou moins) l'infini.
• Asymptote
horizontale. - Si, lorsque x tend vers (plus ou moins) l'infini, f(x) tend
vers une valeur finie b, alors la droite d'Ă©quation y = b est une
asymptote horizontale de la courbe de f.
• Asymptote verticale.
- Si lorsque x tend vers une valeur c, f(x) tend vers (plus ou moins)
l'infini, alors la droite d'Ă©quation x = c est une asymptote verticale
de la courbe de f.
Calcul des dérivées.
Règles
générales.
Les règles à retenir
(analogues à celles que l'on a dites à propos des différentielles),
sont les suivantes :
• Si h(x)
= k.f(x) pour tout x, k Ă©tant une constante, alors h'(x) = k.f'(x).
• Si h(x) = f(x)
+ g(x) pour tout x, alors h'(x) = f'(x) + g'(x).
• Si h(x) = f(x).g(x)
pour tout x, alors h'(x) = f'(x).g(x)+f(x).f'(x). [dérivée du produit]
• Si h(x) = 1/f(x)
et f(x) 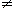 0 pour tout x, alors h'(x) = -f'(x).(f(x))². [dérivée de la fonction
réciproque]
0 pour tout x, alors h'(x) = -f'(x).(f(x))². [dérivée de la fonction
réciproque]
• Si h(x) = f(x)/g(x)
et g (x) 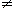 0 pour tout x, alors h' (x) = (f'(x).g(x)- f(x).g'(x))/(g(x))². [Dérivée
du quotient]
0 pour tout x, alors h' (x) = (f'(x).g(x)- f(x).g'(x))/(g(x))². [Dérivée
du quotient]
• Si h(x) = (gof)(x)
= g(f(x)) pour tout x; alors h' = g'(f(x)).f'(x).
Exemples
de dérivées de fonctions usuelles.
Le tableau ci-dessous
donne quelques exemples de fonctions dérivées de fonctions usuelles.
Leur connaissance est utile pour le calcul de dérivées d'autres fonctions.
Dérivées de
fonctions usuelles
Fonction
f(x) |
Dérivée
f'(x) |
c
(constante)
x
cx
1/x
xc
ecx
In
x
ax
(a>0) |
0
1
c
-1/x²
c
xc-1
cecx
1/x
ax
ln
a |
|
Fonction
f(x) |
Dérivée
f'(x) |
rac
(x)
sin
x
cos
x1
tan
x1
cotan
x1
arcsin
x
arccos
x
arctg
x |
½.
1/rac (x)
cos
x
-sin
x1
1/cos²
x1
cos²
x1
1/rac(1-x²)
-1/rac(1-x²)
1/(1+x²) |
|
Note
: rac =  (racine carrée).
(racine carrée).
Théorèmes de
Rolle, de Lagrange et de Cauchy.
Le théorème de
Rolle, le théorème de Lagrange et le théorème de Cauchy concernent
les fonctions continues et dérivables sur un intervalle compact, et jouent
un rôle important dans la démonstration de nombreux théorèmes du calcul
différentiel et intégral. Ces trois théorèmes ont à voir avec les
valeurs intermédiaires que prend une fonction sur un intervalle. Le théorème
de Rolle est un préalable au théorème de Lagrange; le théorème de
Cauchy en est une extension.
Théorème
de Rolle.
Le théorème de
Rolle
énonce que pour toute fonction f continue sur un intervalle fermé, l'égalité
des deux bornes de cet intervalle implique l'existence d'au moins un point
de l'intervalle pour lequel la dérivée de f s'annule :
-
a) La
fonction f est continue sur l'intervalle [a, b]
b) f
est dérivable sur l'intervalle [a, b]
c)
f(a) = f(b) |
|
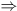 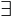 c
c 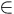 [a, b], tel que f'(c)
= 0 [a, b], tel que f'(c)
= 0 |
Théorème
de Lagrange ( = théorème de la valeur moyenne).
-Si
f est une fonction est continue sur un intervalle fermé [a, b] et 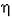 est un nombre réel tel que f (a) <
est un nombre réel tel que f (a) < 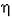 < f (b), il existe un point c de l'intervalle ]a, b[ dans tel que
f (c) =
< f (b), il existe un point c de l'intervalle ]a, b[ dans tel que
f (c) = 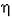 . .
-
a) f
est continue sur [a, b]
b) f
est dérivable sur ]a, b[ |
|
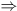 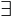 c
c 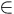 ]a, b[, tel que f'(c)
= [f(b)-f(a)]/(b-a) ]a, b[, tel que f'(c)
= [f(b)-f(a)]/(b-a) |
Théorème
de Cauchy.
Le théorème de
Cauchy
Ă©nonce que le quotient de diviseur non nul de l'accroissement de deux
fonctions continues sur l, un intervalle fermé, et avec des dérivées
uniques sur cet intervalle, non simultanément nulles ni infinies, est
égal au quotient des valeurs de celles-ci en un point intermédiaire.
---
a) f
est continue sur [a, b]
b) f
et g sont dérivables sur ]a, b[;
f'(z) 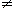 0, 0, 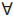 z
z 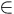 ]a, b[ ]a, b[ |
|
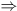 |
|
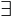 c
c 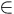 ]a, b[, tel que ]a, b[, tel que
g'(c)/f'(c) = [g(b)-g(a)]/[f(b)-f(a)] |
Deux
autres théorèmes.
Théorème
de Bolzano. - Si une fonction f est continue sur l'intervalle fermé
[a, b] et prend des valeurs de signes opposés aux extrémités dudit intervalle,
il existe au moins une valeur x appartenant Ă l'intervalle l'intervalle
]a, b[ et telle que que f(x) = 0.
• Théorème
de Darboux. - Si une fonction f est continue
sur l'intervalle fermé [a, b], et que que f (a)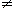 f (b), alors, elle prend toutes les valeurs y telles que f (a)
f (b), alors, elle prend toutes les valeurs y telles que f (a) 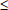 y
y 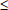 f (b). f (b).
Règle de
L'HĂ´pital.
On a dit plus haut
qu'il peut apparaître dans le calcul de limites des expressions dites
formes indéterminées (des types  - - ,
0/0, etc.). Dans certains cas, l'indétermination peut être levée par
des manipulations algébriques (= par l'application de procédés ou d'opérations
ordinaires de l'algèbre). Dans d'autres cas, de telles manipulations ne
suffisent pas. On recours alors généralement à un théorème, appelé
la règle de L'Hôpital (ou de (Johann) Bernoulli-L'Hôpital),
qui, sous certaines conditions, permet de lever l'indétermination. ,
0/0, etc.). Dans certains cas, l'indétermination peut être levée par
des manipulations algébriques (= par l'application de procédés ou d'opérations
ordinaires de l'algèbre). Dans d'autres cas, de telles manipulations ne
suffisent pas. On recours alors généralement à un théorème, appelé
la règle de L'Hôpital (ou de (Johann) Bernoulli-L'Hôpital),
qui, sous certaines conditions, permet de lever l'indétermination.
La règle de De l'Hôpital
concerne en propre la levée des formes indéterminées 0/0 et  / / .
Pour lever les autres formes indéterminées on devra réécrire
l'expression dont on cherche la limite de telle sorte ces deux formes apparaissent. .
Pour lever les autres formes indéterminées on devra réécrire
l'expression dont on cherche la limite de telle sorte ces deux formes apparaissent.
---
*Avec
un changement approprié du domaine de définition.
Remarques :
• La règle
de L'HĂ´pital est aussi applicable si x, au lieu de de tendre vers une
valeur finie c, tend vers ± ,
à condition que f et g soient dérivables sur ]k, + ,
à condition que f et g soient dérivables sur ]k, + [ ou ]-
[ ou ]- , -k[, oĂą
k est un réel positif. , -k[, où
k est un réel positif.
• La règle est
encore applicable dans le cas oĂą toutes les limites sont seulement Ă
droite (ou Ă gauche). Dans ce cas c peut ĂŞtre Ă©gal Ă a ou Ă b.
• L'indétermination
n'est pas toujours levée par une seule dérivation. Il convient alors
de réitérer la règle de L'Hôpital, c'est-à -dire de dériver la fonction
autant de fois que nécessaire pour lever l'indétermination.
Principes de l'Ă©tude
d'une fonction numérique.
Etudier une fonction
signifie en déterminer le maximum de propriétés. On doit, pour commencer
en spécifier le domaine de définition. Il est utile ensuite de chercher
à identifier les symétries (la fonctions est-elle paire ou impaire, périodique,
etc.). cela permet de réduire l'étude à seulement un sous-ensemble du
domaine de définition. On peut, à partir de là , commencer l'étude proprement
dite : la fonction est-elle continue et sur quels intervalles? Si c'est
le cas, quelles sont ses limites aux bornes des intervalles oĂą elle est
continue? On Ă©tude ensuite le sens de variation; l'outil principal ici
étant une discussion sur le signe de la dérivée. L'ensemble des résultats
obtenus à ce point peut se synthétiser sous la forme du tableau de variation
de la fonction. D'autres éléments peuvent être ajoutés éventuellement
Ă cette Ă©tude : l'Ă©tude des branches infinies et des asymptotes, la
détermination des points remarquables tels que les points d'inflexion.
On termine par la représentation graphique de la fonction.
Calcul intégral
Le calcul intégral
a deux versants qui peuvent s'aborder au travers des notions d'intégrale
définie et de primitive.
• L'intégrale
définie d'une fonction f n'est pas une fonction, mais un nombre
associé à cette fonction sur un intervalle donné : ce nombre fait référence
à l'effet total ou cumulé d'un processus de changement, à ce que l'on
appellera ici, faute de meilleur terme, l' « accumulation» d'une certaine
quantité (définie par f) dans ledit intervalle.
• Les primitives
d'une fonction, quant Ă elles sont des bien fonctions : elles se
déterminent par une opération inverse à celle de la dérivation : on
appelle primitive de la fonction f toute fonction dont la dérivée est
f.
Dans l'un et l'autre
cas, l'opération par laquelle on obtient le résultat cherché s'appelle
une intégration.
Par sa définition
même, la notion de primitive fait le lien entre le calcul intégral et
le calcul différentiel. Le lien qui existe entre une primitive et
une intégrale définie est plus difficile à appréhender.
On peut comprendre
intuitivement Ă quoi correspond le taux de variation d'une fonction
f en un point. Lorsque quelque chose change selon une loi donnée par f,
le calcul différentiel permet de déterminer à chaque instant, en dérivant
f, l'ampleur du changement : il est donné par la loi f' (dérivée). Mais
de quoi f mesure-t-elle la variation? La réponse est que le calcul intégral
porte, lui, une idée d'accumulation : il sert à exprimer, en intégrant
f, la loi F (primitive) selon laquelle s'accumulent ces changements. Une
fois connue cette loi, il est possible de mesurer cette accumulation entre
deux points donnés, ce qui correspond, donc, à ce qu'on appelle l'intégrale
définie.
Une approche graphique
de l'intégrale définie donnera une meilleure idée de ce dont on parle.
L'intégrale définie.
Soit la courbe représentative d'une fonction
f à une variable réelle considérée sur un intervalle [a, b]. (Dans
cet exemple particulier, la fonction est supposée continue et à valeurs
positives sur l'intervalle). La surface sous-tendue par cette courbe (en
bleu) est l'ensemble des points (x, y) tels tel que x appartient Ă l'intervalle
[a, b] et y appartient à l'intervalle [0, f(x)]. On appelle aire algébrique
la mesure de cette surface.
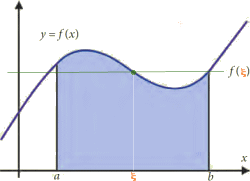
Figure
3. - Aire algébrique sous-tendue par la courbe y = f(x).
(y
est dans cet exemple toujours positif. Mais, dans le cas d'autres fonctions,
des
portions ou même la totalité de la courbe, pourraient aussi,
correspondre
à des y=f(x) négatifs : dans ces portions, on affecterait l'aire
du
signe moins (-), contrairement Ă ce que l'on ferait
pour
calculer une aire géométrique).
Notre propos maintenant est, en s'appuyant
sur le graphique, de déterminer la valeur I de cette aire à partir
de la connaissance de f et de [a, b].
DĂ©termination
de l'aire sous-tendue.
Une valeur approchée de l'aire sous-tendue
s'obtient en choisssant un point d'abscisse 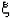 entre a et b, pour ensuite calculer l'aire A sous-tendue par le segment
de la droite d'Ă©quation y = f(
entre a et b, pour ensuite calculer l'aire A sous-tendue par le segment
de la droite d'Ă©quation y = f(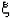 )
entre a et b. Ce calcul est simple, puisqu'on a affaire Ă un rectangle-:
A = f( )
entre a et b. Ce calcul est simple, puisqu'on a affaire Ă un rectangle-:
A = f(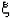 ).(b-a),
mais cette approximation de I est très grossière. ).(b-a),
mais cette approximation de I est très grossière.
On peut faire beaucoup mieux. Au lieu de
considérer l'intervalle [a, b] dans sa totalité, on le subdivise en n
sous-intervalles (ce qui revient à définir une subdivision D = (x0,...
xn) de [a, b]), et l'on calcule l'aire sous-tendue
pour chaque intervalle de la même façon que précédemment. Cela revient
à définir une fonction en escalier 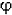 judicieusement «-calée» sur f, est-à -dire
étagée sur la subdivision D, et dont la valeur sur tout intervalle ]xi-1,
xi[ est
judicieusement «-calée» sur f, est-à -dire
étagée sur la subdivision D, et dont la valeur sur tout intervalle ]xi-1,
xi[ est  i
= i
= 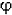 (i)
= f( (i)
= f(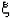 i), i), 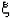 i,
étant un réel quelconque de l'intervalle ]xi-1,
xi[. Une telle fonction en escalier est appelée
fonction
de Riemann relative Ă f. i,
étant un réel quelconque de l'intervalle ]xi-1,
xi[. Une telle fonction en escalier est appelée
fonction
de Riemann relative Ă f.
On pourra ensuite calculer l'aire sous-tendue
par la courbe représentative de 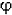 ,
qui est la somme des aires sous-tendues par chaque morceau de cette courbe. ,
qui est la somme des aires sous-tendues par chaque morceau de cette courbe.
Figure
4 - Approximation de f (en bleu)
par
une fonction en escalier (en vert).
Chaque
subdivision de la fonction en escalier est identifiée
par
un indice (un entier positif) i, compris entre 1 et n.
L'aire sous-tendue correspondant Ă la
subdivision i (la marche de notre escalier en vert sur le graphique) est
:
f(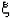 i).(xi-xi-1),
soit i).(xi-xi-1),
soit  i.(xi-xi-1) i.(xi-xi-1)
Et, en utilisant le symbole 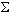 (= somme), la somme I(
(= somme), la somme I(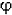 )
des aires de chaque morceau peut alors s'exprimer comme suit : )
des aires de chaque morceau peut alors s'exprimer comme suit :
I(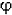 )
= )
=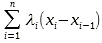
Le réel I(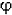 )
défini comme la somme de tous les produits )
défini comme la somme de tous les produits  i.(xi-xi-1),
pour i variant de 1 à n, est aussi appelé intégrale de i.(xi-xi-1),
pour i variant de 1 à n, est aussi appelé intégrale de 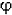 sur [a, b], ou somme de Riemann relative à f, ou encore,
intégrale
au sens de Riemann de la fonction en escalier
sur [a, b], ou somme de Riemann relative Ă f, ou encore,
intégrale
au sens de Riemann de la fonction en escalier 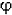 sur [a, b].
sur [a, b].
 Note
: rien ne contraint la subdivision de l'intervalle [a, b], et, partant,
rien n'oblige Ă choisir une mĂŞme largeur pour chaque marche, c'est ce
qui nous fait conserver l'indice i attaché à cacune d'elle. Mais rien
n'interdit non plus de considérer ces marches comme égales. Note
: rien ne contraint la subdivision de l'intervalle [a, b], et, partant,
rien n'oblige Ă choisir une mĂŞme largeur pour chaque marche, c'est ce
qui nous fait conserver l'indice i attaché à cacune d'elle. Mais rien
n'interdit non plus de considérer ces marches comme égales.  xi
peut
alors s'Ă©crire xi
peut
alors s'Ă©crire  x,
ce qui, sans rien changer au fond, allègera la discussion à venir et,
déjà , l'écriture. La formule précédente pourra alors s'écrire : x,
ce qui, sans rien changer au fond, allègera la discussion à venir et,
déjà , l'écriture. La formule précédente pourra alors s'écrire :
I(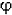 ) ) 
A ce point, on ne dispose encore, avec I(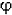 ),
que d'une valeur approche de l'aire I sous-tendue par la courbe représentative
de f : I( ),
que d'une valeur approche de l'aire I sous-tendue par la courbe représentative
de f : I(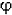 ) ) 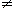 I. Mais la solution est désormais à portée de main : elle tient en un
passage
Ă la limite.
I. Mais la solution est désormais à portée de main : elle tient en un
passage
Ă la limite.
L'intégrale
définie. Définition et notation.
L'approximation de f par 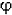 est d'autant meilleure que le nombre de subdivisions n tend vers l'infini
(n
est d'autant meilleure que le nombre de subdivisions n tend vers l'infini
(n  + + ),
autrement dit que la différence ),
autrement dit que la différence  x
tend vers zéro. x
tend vers zéro.
On définit alors I , comme la limite de
la somme de Riemann relative Ă f (entre i=1 et n) quand  x x  0 (quand
0 (quand  x x  0, on convient de noter cette quantité dx) :
0, on convient de noter cette quantité dx) :
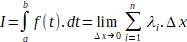
I , somme de a Ă b
de f(t).dt, est l'intégrale (au sens de Riemann) de la fonction
f sur l'intervalle [a, b].
--
Dans l'expression 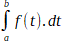 |
|
a
et b sont les limites d'intégration.
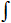 est
l'intégrateur. (C'est l'opérateur associé à est
l'intĂ©grateur. (C'est l'opĂ©rateur associĂ© Ă
l'intégration).
f(t)
est l'intégrande.
dt
est la différentielle de t et indique la variable
par rapport
à laquelle f est dérivée. |
 Note
sur les variables muettes : dans l'expression ci-dessus la variable t (au
même titre que x dans l'expression précédente) est appelée une variable
muette. Elle est nécessaire à la cohérence de l'expression de l'intégrale,
mais aucune valeur ne peut leur être assignée pour effectuer un calcul.
La valeur de l'expression dépend des limites d'intégration et de la fonction,
pas de t. Note
sur les variables muettes : dans l'expression ci-dessus la variable t (au
même titre que x dans l'expression précédente) est appelée une variable
muette. Elle est nécessaire à la cohérence de l'expression de l'intégrale,
mais aucune valeur ne peut leur être assignée pour effectuer un calcul.
La valeur de l'expression dépend des limites d'intégration et de la fonction,
pas de t.
Interprétation
de l'intégrale définie.
On a utilisé plus haut le terme vague
et général d'accumulation pour interpréter la signification d'une intégrale.
C'est bien cette mĂŞme signification qui est sous-jacente
à la manière de définir une intégrale à partir d'une sommation, qu'elle
soit symbolisée par 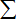 (cas de la sommation de quantités discrètes) ou par
(cas de la sommation de quantités discrètes) ou par 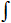 (cas de la sommation de quantités infinitésimales). Les intégrales portent
ainsi toujours en elles cette même idée, qui peut se décliner de diverses
manières. Voici quelques exemples-
:
(cas de la sommation de quantités infinitésimales). Les intégrales portent
ainsi toujours en elles cette même idée, qui peut se décliner de diverses
manières. Voici quelques exemples-
:
• Comment calculer une surface
ou le volume d'une figure géométrique, c'est-à -dire d'une figure dont
les contours peuvent être définis par une fonction? De le même façon
qu'on a calculé l'aire sous-tendue par la courbe d'une fonction, le résultat
cherché pourra être obtenu par une intégration.
Il est Ă noter que, bien avant
l'élaboration du calcul intégral, Archimède
put calculer des aires de figures géométriques (par exemple l'aire sous-tendue
par une parabole), avec une approximation aussi grande que voulue, en utilisant
un procédé (la méthode d'exhaustion, dont l'invention est attribuée
Ă Eudoxe) qui consiste Ă faire la somme d'aires
de figures faciles Ă calculer de plus en plus petites.
• La dépense d'un ménage pour ses
courses peut être modélisée par une fonction en escalier c(i) (chaque
Ă©chelon correspondant Ă un acte d'achat). A la fin du mois, quelle somme
totale aura été dépensée? La réponse sera donnée par le calcul d'une
intégrale.
• Un véhicule se déplace à une certaine
vitesse, fonction du temps v(t). A un instant donné, quelle distance L
aura-t-il parcouru, combien de kilomètres aura-t-il accumulé? La réponse
sera aussi donnée par le calcul d'une intégrale.
• De l'eau se déverse dans un récipient
selon un débit qui est fonction du temps r(t). A un instant donné, quel
sera le volume V d'eau accumulée dans le récipient? Ici encore réponse
sera donnée par le calcul d'une intégrale.
• L'énergie
reçue du Soleil par un panneau solaire varie en fonction des saisons,
de l'alternance du jour et de la nuit et de la couverture nuageuse. Au
bout d'un an, combien d'énergie, susceptible d'être transformé en électricité,
aura-t-il reçu? La réponse (qui en l'occurence n'aura qu'une valeur statistique
à cause des aléas météorologiques), pointe une fois de plus vers un
recours au calcul intégral.
• Une culture de bactéries
se développe à un taux variable. Ici encore, le calcul intégral pourra
être utilisé pour calculer la quantité de bactéries au bout d'une certaine
durée.
Propriétés des
intégrales.
On dit qu'une fonction f est intégrable
au sens de Riemann sur un intervalle [a, b], si et seulement si il existe
un unique réel If tel que quel que soit  > 0, il existe
> 0, il existe 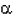 tel que quelle que soit
tel que quelle que soit 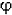 ,
une fonction de Riemann relative à f, de pas strictement inférieur à ,
une fonction de Riemann relative à f, de pas strictement inférieur à 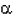 ,
la somme de Riemann correspondante diffère de If de
moins de ,
la somme de Riemann correspondante diffère de If de
moins de  . .
v Toute fonction continue ou monotone
par intervalles sur [a, b] (cela concerne aussi les fonctions en escalier)
sont intégrables au sens de Riemann sur [a, b].
Les fonctions (f, g, ...) intégrables au
sens de Riemann sur un intervalle [a, b] possèdent les propriétés suivantes
:
Somme
de deux intégrales de fonctions.
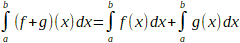
Produit
d'une intégrale par une constante réelle K.

Relation
de Chasles.
.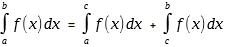 ,
pour tout c ,
pour tout c 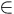 [a, b] [a, b]
Certaines conventions de notation reposent
sur cette propriété; ainsi, si on change les bornes d'intégration, le
signe de l'intégrale change :
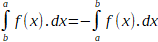
Lorsque les bornes d'intégration sont égales,
l'intégrale est égale à 0 :
Comparaisons
d'intégrales. Monotonie.
Si f(x) 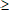 g(x), alors :
g(x), alors : 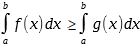
Si f(x) 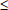 g(x), alors :
g(x), alors : 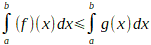
Si f(x) 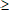 g(x), alors :
g(x), alors : 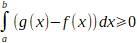
Théorème
de la moyenne.
Si f est continue
sur l'intervalle, alors 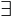 c
c 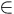 [a,b]
tel que : [a,b]
tel que :
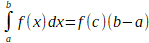 , ,
soit :

Primitives et intégrales
indéfinies.
Avec une intégrale
définie, on s'intéresse à un nombre, qui dans notre exemple, est l'aire
d'une surface sous-tendue par la courbe d'une fonction entre deux constantes,
a et b. Elle fournit ainsi une image statique de l'idée d'accumulation.
Mais l''idée d'accumulation peut s'aborder aussi d'une manière plus dynamique
en faisant varier une des bornes de l'intégrale définie : disons que
la constante b est maintenant remplacée par la variable x, et que l'on
fait varier celle-ci à partir de x = a. Il apparaît alors que l'aire
sous-tendue varie aussi.
En susbstituant la variable x Ă la constante
b, on changé la nature de l'intégrale de la fonction f considérée.
Celle-ci n'est plus une intégrale définie, un nombre I dont la valeur
dépend de deux constantes a et b. C'est devenu une fonction intégrale
indéfinie, autrement dit une fonction F dont la valeur dépend de
la variable x.
Si f est une fonction réelle intégrable
sur [a, b], la fonction F : [a, b]  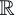 définie par :
définie par :
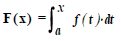
reçoit le nom de fonction
intégrale indéfinie ou fonction intégrale de f correspondant
au point a.
La fonction intégrale
indéfinie s'obtient à partir de l'intégrale définie en rendant la limite
supérieure de l'intégrale x variable, tout en conservant la limite inférieure
fixe.
 Notez
bien ici que x est la seule variable sur laquelle agisse la fonction; comme
on l'a remarqué plus haut, t est une variable muette... et n'a donc pas
son mot Ă dire en l'occurence. Notez
bien ici que x est la seule variable sur laquelle agisse la fonction; comme
on l'a remarqué plus haut, t est une variable muette... et n'a donc pas
son mot Ă dire en l'occurence.
On va montrer f est
la dérivée de F. Il suffit pour cela de dériver F, ou plus précisément
de chercher la valeur F'(x0) de la dérivée de F
en x0. En revenant à la définition de la dérivée,
on pourra Ă©crire pour F' :
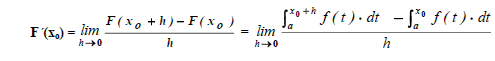 d'oĂą :
d'oĂą :

Le premier et le troisième terme de la
somme s'annulent et le théorème de la valeur moyenne assure de l'existence
d'un nombre c dans l'intervalle [x0, x0+h]
si h >0 (ou [x0+h, x0] si h <0]
) tel que :
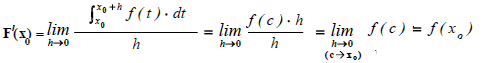
(La démonstration ci-dessus
ne vaut en réalité que pour x0 appartenant à l'intervalle
]a, b[, mais, pour x0 = a ou x0
= b, il suffira de considérer respectivement les limites quand h 0-
ou quand h 0-
ou quand h 0+). 0+).
La dérivée de F est bien f comme attendu.
On dit que F est une primitive de f :
• Soit
une fonction f : [a, b]   , on donne le nom de primitive de f Ă toute fonction F : [a, b]
, on donne le nom de primitive de f à toute fonction F : [a, b]   dérivable sur l'intervalle [a, b] et dont la dérivée est f dans ce même
intervalle. Autrement dit : F'(x) = f (x),
dérivable sur l'intervalle [a, b] et dont la dérivée est f dans ce même
intervalle. Autrement dit : F'(x) = f (x),  x x  [a, b] .
[a, b] .
Toutes les fonctions
n'ont pas de primitives; seules les fonctions intégrables en possèdent.
On remarquera encore
que si F(x) est une primitive d'une fonction f (x), alors la différentielle
dF est donnée par dF = F'(x).dx = f(x).dx. Ce qui permet d'écrire :

On retrouve ici l'idée
énoncée plus haut à partir d'une intuition graphique que l'intégrale
(symbolisée par 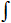 )
correspond bien à une sommation d'un continuum de quantités infinitésimales. )
correspond bien à une sommation d'un continuum de quantités infinitésimales.
Théorème
fondamental de l'analyse.
Le paragraphe précédent
atteste de l'existence d'un lien entre différenciation et intégration.
Reste à voir comment exploiter ce lien pour calculer des intégrales.
Cela se fait à partir des méthodes fournies par le théorème fondamental
du calcul intégral. Avant de l'énoncer, il convient de mettre en exergue
plusieurs propriétés des primitives et des fonctions intégrales définies.
Les primitives d'une
fonction remplissent les conditions suivantes:
• Si F
est une primitive de f dans [a, b], alors elle admet comme primitives les
fonctions G(x) = F(x) + C, où C est une valeur réelle quelconque. (Cela
vient de ce que la dérivée d'une fonction constante est nulle).
• Si une fonction
a une primitive alors elle admet une infinité de primitives. (C'est la
conséquence directe de la proposition précédente, puis C peut prendre
une infinité de valeurs).
• Si F et G sont
des primitives de la mĂŞme fonction f sur [a, b], alors il existe une constante
C telle que F(x) - G(x) = C,  x x  [a, b].
[a, b].
• L'ensemble de
toutes les primitives de f est appelé l'intégrale indéfinie de
f et est noté 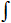 f (x).dx. Soit :
f (x).dx. Soit :
.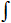 f(x).dx
= F(x) + C. f(x).dx
= F(x) + C.
 RĂ©capitulatif
du vocabulaire : l'intégrale définie est un nombre; la fonction
intégrale indéfinie est une fonction considérée en tant que primitive
d'une fonction donnée; l'intégrale définie est une classe ou
un ensemble de fonctions (toutes les primitives d'une fonction données,
qui ne diffèrent entre elles que par une constante). Récapitulatif
du vocabulaire : l'intégrale définie est un nombre; la fonction
intégrale indéfinie est une fonction considérée en tant que primitive
d'une fonction donnée; l'intégrale définie est une classe ou
un ensemble de fonctions (toutes les primitives d'une fonction données,
qui ne diffèrent entre elles que par une constante).
Les fonctions intégrales
indéfinies, quant à elles, ont des propriétés importantes qui dépendent
de la fonction à intégrer :
• Si f
est intégrable sur un intervalle compact, alors F est continue sur cet
intervalle.
• Si f est continue
sur [a, b], alors F est dérivable sur [a, b] et sa dérivée est F'(x)
= f (x), 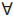 x x 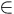 [a, b].
[a, b].
Ce dernier énoncé
constitue le premier théorème fondamental de l'analyse
(ou
premier
théorème fondamental du calcul intégral).
Notez que quelle
que soit la valeur prise par a, on aura :
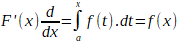
De plus, lorsque f est
continue (une condition requise par le théorème fondamental du calcul
intégral), les concepts de primitive et de fonction intégrale indéfinie
coïncident, bien qu'ils aient été définis différemment.
• Si f
est continue, elle admet des primitives mais si elle cesse d'ĂŞtre continue
à un moment donné de l'intervalle, même si elle continue d'être intégrable
(et admet donc une intégrale indéfinie), elle peut ne pas admettre de
primitives.
Une conséquence immédiate
du premier théorème fondamental du calcul est qu'il nous fournit une
méthode pratique pour calculer des intégrales, c'est-à -dire pour trouver
des primitives. Voyons un corollaire pour lequel l'existence des primitives
est supposée connue :
• Règle
de Barrow. Si f : [a, b]   est continue sur l'intervalle de définition et si G : [a, b]
est continue sur l'intervalle de définition et si G : [a, b]   est une primitive de f sur ledit intervalle, alors on vérifie que :
est une primitive de f sur ledit intervalle, alors on vérifie que :
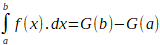
 Remarque
: la différence G(b) - G(a) est ordinairement notée : Remarque
: la différence G(b) - G(a) est ordinairement notée : 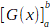
Sous certaines conditions,
la règle de Barrow continue à être valable même si f n'est pas continue.
On peut alors dire que :
Si une fonction
f est intégrable sur l'intervalle [a, b] : et si G est une primitive
de f sur [a, b], alors on a :
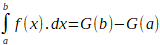
• Ainsi conditionnée,
cette dernière expression correspond au deuxième théorème fondamental
du calcul intégral ou théorème fondamental du calcul intégral
(ou de l'analyse) proprement dit.
Méthodes d'intégration.
Le calcul intégral
est en règle générale beaucoup plus difficile que le calcul différentiel
et le calcul d'une primitive peut être très laborieux. On donnera plus
loin quelques méthodes permettant de se tirer d'embarras dans de nombreuses
siuations, mais il est déjà possible de déduire plusieurs résultats
des propriétés déjà établies par le calcul différentiel entre les
fonctions et leurs dérivées et, partan,t entre les fonctions et leurs
primitives quand elles existent.
Opérations
sur les primitives.
On considère dans
ce qui suit deux fonctions f et g définies sur un même intervalle J de ,
dérivables sur J (avec pour dérivées f' et g'), un réel ,
dérivables sur J (avec pour dérivées f' et g'), un réel  et un rationnel r
et un rationnel r -1.
On peut déduire des règles générales énoncées plus haut pour les
dérivées, les règles suivantes pour les primitives : -1.
On peut déduire des règles générales énoncées plus haut pour les
dérivées, les règles suivantes pour les primitives :
1°) f+g
primitive sur J de f'+g'
2°)  f
primitive sur J de f
primitive sur J de  f' f'
3°)
fg primitive de f'g+fg'
4°)
f/g primitive sur J de (f'g-fg')/g² (si 1/g définie sur J).
5°)
(fr+1)/(r+1) est une primitive sur J de
f'fr (si fr
est définie sur J).
 La
première règle permet de comprendre que si une fonction possède une
primitive alors elle en possède une infinité. Pour le démontrer, il
suffit de remarquer qu'une fonction constante C(x) = k a pour dérivée
C'(x) = 0, si bien que si F est la primitive de f, alors toutes les
fonctions de type F+C ont aussi pour dérivée f et donc, corrélativement,
si f a pour primitive F elle a aussi pour primitives toutes les fonctions
F+C. La valeur k prend le nom de constante d'intégration. La
première règle permet de comprendre que si une fonction possède une
primitive alors elle en possède une infinité. Pour le démontrer, il
suffit de remarquer qu'une fonction constante C(x) = k a pour dérivée
C'(x) = 0, si bien que si F est la primitive de f, alors toutes les
fonctions de type F+C ont aussi pour dérivée f et donc, corrélativement,
si f a pour primitive F elle a aussi pour primitives toutes les fonctions
F+C. La valeur k prend le nom de constante d'intégration.
Primitives
de fonctions usuelles.
Les fonctions dont on peut donner une
primitive sans presque aucun calcul sont celles que l'on connaĂ®t dĂ©jĂ
en tant que dérivées.
Il suffit donc de reprendre
un tableau de dérivées usuelles, comme celui donné plus haut par exemple,
et d'en changer les en-tĂŞtes pour disposer Ă peu de frais de quelques
primitives :
Primitives de
fonctions usuelles
Primitive
F(x) |
Fonction
f(x) |
k
(constante)
x
cx
xc
(1/c+1)xc+1
ecx
In
x
ax(a>0) |
0
1
c
cxc-1
xc
cecx
1/x
ax
ln
a |
|
Primitive
F(x) |
Fonction
f(x) |
sin
x
1/a
sin (ax+b)
cos
x1
tan
x1
cotan
x1
arcsin
x
arccos
x
arctg
x |
cos
x
cos
(ax+b)
-sin
x1
1/cos²
x1
cos²
x1
1/rac(1-x²)
-1/rac(1-x²)
1/(1+x²) |
|
Cela semble un résultat
excessivement modeste, mais il peut être très utile si l'on parvient,
par une manipulation algébrique, à ramener (en partie ou en totalité)
l'expression de la fonction dont cherche une primitive Ă une combinaison
de termes ayant une primitive déjà connue. On a donc intérêt,
quand on aborde le calcul intégral, à connaître par coeur un maximum
de dérivées de fonctions usuelles.
Il existe de nombreuses méthodes d'intégration
qui permettent d'aller plus loin. Certaines concernent certains types de
fonctions (trigonométriques, exponentielles, polynomiales, etc.), d'autres,
comme les deux qui suivent, sont plus générales. Avec un de la pratique,
lorsqu'elles sont applicables, elles peuvent simplifier considérablement
le travail d'intégration.
Intégration
par substitution.
Soient f, une fonction intégrable sur
l'intervalle [a, b], et g, une fonction dérivable et de dérivée continue
sur l'intervalle [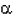 , , 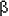 ],
avec ],
avec 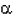 = g-1 (a),
= g-1 (a), 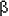 = g-1 (b) et g([
= g-1 (b) et g([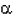 , , 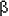 ])
= [a, b]. On peut Ă©crire alors, dans le cas
de l'intégrale définie : ])
= [a, b]. On peut Ă©crire alors, dans le cas
de l'intégrale définie :
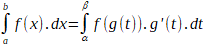
Si l'on s'en tient à considérer l'intégrale
indéfinie, cela devient :
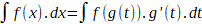
A première vue, il
semblerait qu'on n'a fait qu'ajouter des complications Ă quelque chose
qui d'emblée n'était déjà pas très simple. En réalité, cette formule
permet de se tirer d'embarras dans de nombreuses situations.
 Exemple
(cas d'une ntégrale indéfinie) : On cherche à intégrer : Exemple
(cas d'une ntégrale indéfinie) : On cherche à intégrer :
. (sin
x)5.cos x.dx (sin
x)5.cos x.dx
1) On pose
sin x = t, dont il suit que cos x.dx = dt
2) Avec ce changement
de variable, l'intégrale devient :  t5.dt,
qui est facile à intégrer (voir le tableau des primitives usuelles). t5.dt,
qui est facile à intégrer (voir le tableau des primitives usuelles).
3) Au final : (sin
x)5.cos x.dx = (sin
x)5.cos x.dx =  t5.dt
= u6/6 + C t5.dt
= u6/6 + C
On constate dans cet
exemple (mais c'est très général) que dans une intégration par substitution,
la principale difficulté réside dans le choix judicieux qui doit être
fait pour le changement de variables.
 Exemple
(cas d'une intégrale définie). - On cherche à intégrer : Exemple
(cas d'une intégrale définie). - On cherche à intégrer :
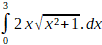
1) On remarque que 2x est la dérivée
de x²+1. On a donc avantage à poser-
: t
= x²+1, dont il suit que dt=2x.dx.
2) Avec ce changement de variable, les
limites deviennent : 1 et 10, et la question posée revient à intégrer
:
.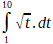 ,
soit : ,
soit : 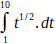
3) On déduit du tableau des primitives usuelles,
que la fonction F : t  2/3.t3/2
est une primitive de la fonction f : t 2/3.t3/2
est une primitive de la fonction f : t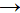 t1/2 .
t1/2 .
4) Le théorème fondamental du calcul
intégral conduit alors à écrire :
.
Intégration
par parties.
L'intégration par
parties repose sur la règle de dérivation d'un produit de fonctions.
Soient f et g deux
fonctions continues possédant des dérivées continues sur l'intervalle
[a, b]. Le produit f.g est une primitive de (f.g)'. On a vu plus haut que
: (f.g)' = f.g'+f'.g. Le poroduit f.g est donc une primitive de f.g'+f'g.
Cela est vrai aussi pour tout intervalle [a, x] inclus dans [a,b]. Il est
alors possible d'Ă©crire, pour tout x appartenant Ă [a, b] :
Autrement dit :

Lorsque x=b , la relation
exprime la valeur de l'intégrale définie :

On parle d'intégration par parties, lorsque
on applique cette relation pour calculer une primitive de f.g', au lieu
de calculer une primitive de f'.g. On peut chercher à utiliser cette méthode
chaque fois que l'on a Ă faire au produit de deux fonctions et que le
résultat n'est pas trivial; son l'intérêt apparaît plus clairement
quand les primitives de f.g' sont plus faciles Ă trouver que celles de
f'.g.
 Exemple
: On cherche à intégrer Exemple
: On cherche à intégrer  x.sin
x dx. x.sin
x dx.
1) On pose : f(x) = x et dg(x)
= sin x.dx (soit g'(x) = sin x).
2) D'où (d'après les tableaux donnés
précédemment) : f'(x) = 1 et g (x) = -cos x.
3) Il suffit d'appliquer la formule de
l'intégration par parties pour obtenir :
Il est possible qu'une seule intégration
par parties ne permette pas de résoudre le problème posé, et qu'il faille
réitérer le calcul sur la partie restant exprimée sous la forme
d'une intégrale.
 Exemple
: On cherche à intégrer Exemple
: On cherche à intégrer  x².ex.dx. x².ex.dx.
1) On pose : f(x)=x² et dg(x)
= ex.dx.
2) D'oĂą : df(x)=2x.dx et g(x) = ex.
3) Et donc, en appliquant la formule de
l'intégration, par parties :
=== x².ex.dx
= x².ex - 2. x².ex.dx
= x².ex - 2. x.ex.dx. x.ex.dx.
4) D'oĂą f1 = x1
et df1 = dx; dg1= ex.dx,
g1 = ex.
5) L'intégration par parties donne :
. x.ex.dx
= x.ex - x.ex.dx
= x.ex -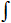 ex.dx
= x.ex - ex
+
C ex.dx
= x.ex - ex
+
C
6) Au final :
.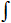 x².ex.dx=x².ex-2(x.ex
-ex)+C=x².ex-2x.ex+2ex+C x².ex.dx=x².ex-2(x.ex
-ex)+C=x².ex-2x.ex+2ex+C
soit, en factorisant :
.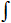 x².ex.dx
= ex. (x²-2x+2) + C. x².ex.dx
= ex. (x²-2x+2) + C.
Les deux exemples précédents concernaint
seulement des intégrales indéfinies. Lorsqu'on a affaire à une intégrale
définie, une bonne stratégie consiste a d'abord évaluer l'intégrale
indéfinie et seulement ensuite à évaluer les limites.
Généralisation
de la notion d'intégrale.
Intégrales
au sens de Riemann.
Dans cette page on ne traite que de l'intégrale
au sens de Riemann. Comme on l'a vu plus
haut il s'agit de l'intégrale d'une fonction bornée et définie sur un
intervalle fermé et adossée à la définition d'une unique fonction escalier
dont elle est la limite.
Intégrales
au sens de Stieltjes.
Un autre type d'intégrale est définie
à partir de deux fonctions f et g définies sur un intervalle fermé comme
dans le cas de l'intégrale de Riemann. Mais ici l'intégrale est construite
Ă partir de la somme : 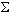 f(
f(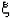 i).[g(xi)-g(xi-1)].
Si lorsque les sous-intervalles tendent vers zéro la limite existe (indépendamment
du choix des points xi et i).[g(xi)-g(xi-1)].
Si lorsque les sous-intervalles tendent vers zéro la limite existe (indépendamment
du choix des points xi et 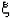 i),
alors cette limite est appelée intégrale au sens de Stieltjes
(ou intégrale au sens de Riemann-Stieltjes). L'intégrale de Riemann correspondant
au cas ou g(x) = x. i),
alors cette limite est appelée intégrale au sens de Stieltjes
(ou intégrale au sens de Riemann-Stieltjes). L'intégrale de Riemann correspondant
au cas ou g(x) = x.
Intégrales
impropres.
Lorsqu'on a des intégrales avec des limites
d'intégration infinies ou des intégrales avec des intégrants
non bornés, on parle d'intégrales impropres.
Intégrales
au sens de Lebesgue.
Mentionnons encore pour mémoire l'intégrale
au sens de Lebesgue, dont la notion relève de l'étude générale
de l'analyse fonctionnelle. Elle est plus difficile d'accès et fait appel
aux notions de la théorie de la mesure. Le domaine d'intégration implique
des sous-ensembles de  n
partitionnés en sous-ensembles mesurables. n
partitionnés en sous-ensembles mesurables. |
|