| . |
|
||||||
|
|
| . |
|
||||||
| La pensée et ses outils > Logique et théorie de la connaissance > Mathématiques > Algèbre |
L'algèbre
linéaire est un domaine des mathématiques qui étudie les vecteurs,
les espaces vectoriels, les transformations linéaires et les systèmes
d'équations linéaires. Elle est fondamentale dans de nombreux domaines
scientifiques et techniques, comme l'informatique, la physique, l'ingénierie,
l'économie et bien d'autres.
Notions générales sur les vecteursUn vecteur est une entité mathématique qui combine deux caractéristiques essentielles : une magnitude (norme ou module) et un sens. Dans cette page, on notera les vecteurs en gras. Dans le contexte de l'algèbre linéaire, les vecteurs sont principalement utilisés pour représenter des points dans un espace ou des grandeurs orientées, c'est-à -dire ayant un sens. En algèbre linéaire, un vecteur est une liste ordonnée de nombres, appelée composantes ou coordonnées du vecteur. Ces nombres décrivent la position d'un point ou une direction dans un espace. Par exemple, en 2 dimensions : v=(x,y); en 3 dimensions : v= (x, y, z); en n dimensions : v=(v1, v2,..., vn).Représentation
géométrique.
Vecteur
en 2D.
Vecteur
en 3D.
Norme
(magnitude).
Le
sens.
Opérations sur
les vecteurs.
L'addition de deux vecteurs (et a fortiori de plusieurs vecteurs) possède plusieurs propriétés importantes : ⢠Fermeture. - L'addition de deux vecteurs quelconques de E est un vecteur de E : u+vGrâce à la commutativité et l'associativité, on peut réarranger les termes d'une somme de vecteurs à notre convenance pour faciliter les calculs. L'existence d'un élément neutre et, pour tout vecteur, celle d'un vecteur opposé permet de définir la soustraction (notée -) de deux vecteurs : La soustraction d'un vecteur est définie comme l'addition de son opposé : u - v = u + (-v). Multiplication
par un scalaire.
La multiplication
scalaire est associative (k(l.u) = (kl).u), distributive
par rapport à l'addition vectorielle (k.(u + v) = k.u
+ k.v) et distributive par rapport à l'adition des scalaires ((k
+ l.).u = k.u + l.u). Il existe dans l'ensemble K
un élément neutre (noté ici 1), tel que pour tout l'élément
u
de E, on ait 1.u = u et u.1 = u, et un élément
abosrbant (noté 0), tel que que pour tout u Autres
opérations.
⢠Produit scalaire. - Le produit scalaire (noté .) est une opération qui donne un nombre à partir de deux vecteurs. ⢠Produit matriciel (d'un vecteur par une matrice). - Une matrice A de taille m x n multipliée par un vecteur v de dimension n donne un vecteur w de dimension m. Chaque composante de w est le produit scalaire d'une ligne de A par le vecteur v.Exemples d'utilisation des vecteurs. En physique, les vecteurs représentent des grandeurs comme la vitesse, la force, ou l'accélération. En informatique, ils servent à modéliser des données dans des espaces multidimensionnels (comme dans l'apprentissage automatique). En géométrie, ils décrivent des directions et des déplacements. Relations géométriques
entre vecteurs.
Vecteurs
équipollents (égaux).
Vecteurs
orthogonaux (perpendiculaires).
Vecteurs
colinéaires (parallèles).
Vecteurs
opposés.
Espaces vectorielsLa notion d'espace vectoriel est au coeur de l'algèbre linéaire. C'est une abstraction puissante qui sous-tend une grande partie des mathématiques et des sciences modernes. On utilise des espace vectoriels en physique, pour modéliser des forces ou des mouvements dans l'espace. En informatique, on les emploie pour traiter des données en machine learning ou en traitement d'image. En mathématiques, ce sont un outil fondamental pour l'analyse et la résolution d'équations linéaires.Définition.
⢠E est un groupe abélien. - Pour commencer l'addition de deux vecteurs doit être une opération commutative : u+v = v+u,Si ces conditions sont réunies, on dit que E, muni d'une opération interne et d'une opération externe dont le domaine d'opérateurs est K, a une structure d'espace vectoriel sur K, ou que E est un espace vectoriel (sur K), ou encore que E est un K-espace vectoriel. Combinaison linéaire,
indépendance linéaire, base et dimension.
Si v1,
v2,â¦,
vkâ
sont des vecteurs dans V et λ1,λ2,â¦,λk
sont
des scalaires dans K, alors :
Indépendance
linéaire.
Un ensemble de vecteurs
{v1, v2,â¦,vk}
dans V est dit linéairement indépendant si la seule combinaison linéaire
qui donne le vecteur nul est celle où tous les coefficients sont nuls
:
Si au moins un des coefficients peut être non nul dans une telle combinaison donnant le vecteur nul, les vecteurs sont dits linéairement dépendants. Dans ce cas, au moins un des vecteurs peut être écrit comme une combinaison linéaire des autres. Base
d'un espace vectoriel.
Un ensemble de vecteurs
BV = {b1, b2,â¦,
bn}
est une base de l'espace vectoriel V si : a) l'ensemble {b1,
b2,â¦,
bn}
est linéairement indépendant; b) l'ensemble {b1,
b2,â¦,
bn}
engendre V, c'est-à -dire que tout vecteur v Une base est ainsi un ensemble de vecteurs à la fois minimal (aucun vecteur ne peut être retiré sans perdre l'indépendance linéaire) et maximal (aucun vecteur supplémentaire ne peut être ajouté sans perdre l'indépendance linéaire). Dimension d'un espace vectoriel. La dimension d'un espace vectoriel est le nombre de vecteurs dans une base de cet espace. Si V est un espace
vectoriel et {b1, b2,â¦,
bn}
est une base de V, alors la dimension de V est dimâ¡(V)=n. Par exemple, Toutes les bases d'un espace vectoriel ont le même nombre de vecteurs. Dans un espace vectoriel de dimension finie V, tout ensemble linéairement indépendant peut être complété pour former une base. Si dimâ¡(V) = n, alors tout ensemble de n vecteurs linéairement indépendants dans V est une base, et tout ensemble de n vecteurs qui engendrent V est aussi une base. Caractéristique
d'un espace vectoriel.
⢠Un espace vectoriel est dit de caractéristique nulle si p = 0. Cela signifie que la multiplication de 1 par lui-même un nombre quelconque de fois ne donne jamais 0. Les espaces vectoriels des nombres réelsLa caractéristique d'un espace vectoriel détermine les propriétés, telles que a commutativité de la multiplication scalaire, l''associativité de la multiplication scalaire, la distributivité de la multiplication scalaire par rapport à l'addition de vecteurs. Sous-espaces vectoriels.
Un sous-ensemble W d'un espace vectoriel V sur un corps K est un sous-espace vectoriel si les conditions suivantes sont remplies :
W â Propriétés
générales des sous-espaces vectoriels
La somme de deux
vecteurs u,v Le produit d'un vecteur
u.W par un scalaire λ Caractérisation
par combinaison linéaire.
L'ensemble de toutes les combinaisons linéaires de v1, v2,â¦,vk.â forme un sous-espace vectoriel de W appelé espace engendré par {v1,v2,â¦, vk}. Intersection
des sous-espaces.
Somme
des sous-espaces.
Dimension.
Stabilité
par restriction.
Exemples.
L'ensemble des polynômes de degré inférieur ou égal à nn, noté Pn, est un sous-espace vectoriel de l'ensemble des polynômes P. Espace vectoriel
des fonctions réelles.
L'espace vectoriel des fonctions réelles est de dimension infinie. Cela signifie qu'il n'existe pas de base finie pour cet espace. En d'autres termes, on ne peut pas exprimer toutes les fonctions réelles comme une combinaison linéaire d'un nombre fini de fonctions. Il existe de nombreux sous-espaces vectoriels importants dans l'espace des fonctions réelles, tels que : l'espace des fonctions continues, l'espace des fonctions dérivables, l'espace des fonctions intégrables, l'espace des polynômes, l''espace des fonctions périodiques, etc. Applications linéairesLes applications (ou transformations) linéaires sont des fonctions qui transforment des vecteurs tout en conservant les propriétés d'additivité et d'homogénéité . Par exemple, la rotation, l'étirement, ou la réflexion.Définition et
propriétés.
f(u+v)=f(u)+f(v) pour tous u,v
f(λu)=λf(u) pour tout λ Ces propriétés garantissent que f préserve les relations linéaires entre les vecteurs. Image
d'une application linéaire.
L'image de f est un sous-espace vectoriel de W. La dimension de Im(f) est appelée le rang de f, noté rang(f). Noyau
d'une application linéaire.
Le noyau de f est un sous-espace vectoriel de V. Si f est injective, alors Ker(f)={0}. La dimension de Ker(f) est appelée la nullité de f, notée null(f). Théorème du
rang
Interprétation : ⢠rang(f) représente le nombre de dimensions de V qui "contribuent" réellement à l'image.Isomorphismes. En algèbre linéaire, un isomorphisme est une application linéaire qui établit une correspondance biunivoque (bijective) entre deux espaces vectoriels. Soient V et W deux espaces vectoriels sur un même corps K. Une application f:VâW est un isomorphisme d'espaces vectoriels si elle satisfait les conditions suivantes : ⢠Linéarité :Ces deux dernières conditions combinées expriment la bijectivité de f. Si deux espaces vectoriels V et W sont isomorphes, cela signifie qu'ils ont la même structure algébrique, même s'ils peuvent apparaître différents à première vue (par exemple, leurs bases peuvent être différentes). Concrètement, cela revient à dire qu'ils ont la même dimension et les mêmes propriétés algébriques. Les isomorphismes conservent en particulier les opérations d'addition et de multiplication scalaire. Si V et W sont isomorphes, alors ils ont même dimension : dimâ¡(V) = dimâ¡(W). Si f : VâW f est un isomorphisme, alors son inverse fâ1 : WâV est également linéaire. Matrices et représentation des applications linéairesDéfinitions.Définition d'une matrice. Une matrice est un tableau rectangulaire d'éléments, généralement des nombres (et plus largement d'éléments d'un corps K) , disposés en lignes et en colonnes. On la représente entre crochets ou parenthèses. Dimensions
(lignes, colonnes).
L'ensemble des matrices m x n dont les éléments appartiennent à un corps K pourra être noté : Mm x n (K). Types
de matrices.
⢠Matrice carrée. - Une matrice carrée est une matrice avec un nombre égal de lignes et de colonnes (m = n). On parle alors d'une matrice de taille n x n ou d'ordre n. 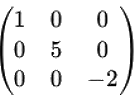 ⢠Matrice triangulaire. - Une matrice triangulaire est une matrice carrée dont tous les éléments au-dessus ou au-dessous de la diagonale principale sont nuls.Notation des éléments d'une matrice. Les éléments d'une matrice sont généralement notés à l'aide d'une lettre minuscule, souvent a, suivie de deux indices. Le premier indice indique le numéro de la ligne, et le second indice indique le numéro de la colonne où se trouve l'élément. Si on a une matrice A de dimension m x n, on note ses éléments comme suit : aij, où : i représente le numéro de la ligne (1 ⤠i ⤠m), et j représente le numéro de la colonne (1 ⤠j ⤠n).
a11 est l'élément situé à la ligne 1 et à la colonne 1, a12 est l'élément situé à la ligne 1 et à la colonne 2, a21 est l'élément situé à la ligne 2 et à la colonne 1, etc. On peut également utiliser d'autres lettres minuscules comme bij, cij, etc., pour représenter les éléments de matrices différentes. L'important est de maintenir une notation cohérente tout au long d'un calcul ou d'une démonstration. La matrice elle-même est généralement représentée par une lettre majuscule (A, B, C, etc.). Opérations sur les matrices. Addition et soustraction de matrices (conditions). L'addition et la soustraction de matrices ne sont définies que pour les matrices de mêmes dimensions. Si deux matrices A et B ont la même dimension m x n, alors leur somme (A + B) et leur différence (A - B) sont également des matrices m x n dont les éléments sont calculés élément par élément. ⢠Addition de matrices. - Soient A et B deux matrices m x n : A = [aij] et B = [bij], alors, la matrice somme C = A + B est définie par : C = [cij] où cij = aij + bij pour tout i et j. ⢠Soustraction de matrices. - La soustraction est similaire à l'addition. Soient A et B deux matrices m x n : A = [aij] et B = [bij]. Alors, la matrice différence D = A - B est définie par : D = [dij] où dij = aij - bij pour tout i et j.L'addition de matrices est commutative (A + B = B + A); associative ((A + B) + C = A + (B + C)), et elle possède un élément neutre: La matrice nulle (de même dimension). Multiplication
d'une matrice par un scalaire.
La multiplication d'une matrice par un scalaire possède les propriétés suivantes : ⢠Associativité. - k.(l.A) = (kl).A où k et l sont des scalaires.Ces propriétés rendent la multiplication scalaire des matrices une opération simple et utile dans de nombreuses applications de l'algèbre linéaire. Produit
de deux matrices.
Si A = [aik] et B = [bkj], alors le produit C = [cij] = AB est une matrice m x p où l'élément cij est calculé comme la somme des produits des éléments correspondants de la i-ème ligne de A et de la j-ème colonne de B : 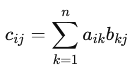 où aikâ est l'élément de la i-ème ligne et k-ième colonne de A, et bkjâ est l'élément de la k-ième ligne et j-ième colonne de B. Propriétés : ⢠Non-commutativité. - En général, AB â BA. L'ordre est crucial. Même si AB et BA sont définies, elles ne sont pas forcément égales.Cas particulier: ⢠Matrice diagonale. - Le produit par une matrice diagonale est simple : il effectue une mise à l'échelle des lignes ou des colonnes selon les valeurs diagonales.Le produit matriciel peut être interprété comme une transformation géométrique. Chaque matrice peut représenter une transformation linéaire (rotation, dilatation, projection, etc.). Le produit de deux matrices représente alors la composition de ces transformations. Par exemple, si A représente une rotation et B une dilatation, alors AB représente d'abord une dilatation suivie d'une rotation. L'ordre est important car la rotation puis la dilatation donnerait un résultat différent (BA). Transposition
d'une matrice.
Propriétés importantes de la transposée : ⢠Transposée de la transposée d'une matrice : (AT)T=AMatrices particulières : ⢠Matrice symétrique. - Une matrice symétrique est une matrice carrée qui est égale à sa transposée (A = AT). Cela signifie que les éléments aij et aji sont égaux pour tous i et j.Inversion d'une matrice. L'inversion d'une matrice A consiste à calculer une matrice inverse notée A-1, telle que A.A-1 = A-1.A = I, où I est la matrice identité. On reviendra plus bas sur les conditions que doir remplir une matrice pour être inversible, et si c'est le cas sur la manière de calculer son inverse. Notons seulement des propriétés importantes de l'inverse : ⢠Inverse de l'inverse d'une matrice : (A-1)-1 = AVecteurs, matrices et applications linéaires. Les paragraphes précédents ont montré la relation entre les vecteurs et les applications linéaires. Il reste a éclaire en quelque mots celle des vecteurs avec les matrices et, par là celle des matrices avec les applications linéaires. On peut voir les vecteurs comme un cas particulier de matrices, et les matrices comme des outils pour manipuler les vecteurs de manière efficace en reconnaissant qu'elles sont une expression des applications linéaires.. Les
matrices sont des vecteurs.
Les
vecteurs sont des matrices.
Cela ressemble Ã
une matrice de dimension n x 1 (comme la première écriture ressemblait
à celle d'une matrice de dimension 1 x n). Nous parlons de ressemblance,
parce que dans la pratique (et cela se justifie par les contextes et les
manières dans lesquels les uns et les autres sont utilisés), on a l'habitude
de distinguer les vecteurs "Ã l'ancienne" de ces "nouvelle sorte de "
de vecteurs que sont les matrices. La distinction se fait par des
différences de notation et de vocabulaire. Un vecteur colonne est ainsi
une matrice composée d'une seule colonne de nombres. Si l'on a un vecteur
v
qui est un élément d'un espace vectoriel, alors le vecteur colonne V
correspondant à v est simplement la représentation de
v
sous forme de matrice colonne. Un vecteur colonne est une matrice de dimension
n x 1, tandis qu'un vecteur ligne est une matrice de dimension 1 x n. Cela
permet d'utiliser les opérations matricielles (addition, multiplication)
sur les vecteurs.
Les
matrices sont l'expression d'applications linéaires.
On peut dès lors voir dans une matrice A l'expression d'une application linéaire f. La multiplication d'une matrice par un vecteur u représente une transformation linéaire du vecteur. On qualifie aussi une telle matrice d'opérateur sur les vecteurs.La matrice décrit cette transformation (rotation, dilatation, cisaillement, etc.), et le vecteur v résultant est l'image du vecteur original après cette transformation. On peut écrire de façon équivalente : f(u) = v, u.A =v et U.A = V, où A est l'expression matricielle de f. Composition
d'applications linéaires et produit matriciel.
La composition gof des deux applications linéaires, définie comme : (gof)(x)=g(f(x)), peut alors s'exprimer termes de matrices comme (gOf)(x)=B.(A.x). Le produit B.(A.x) peut être aussi réécrit comme : (B.A).x,, où B.A est le produit matriciel des matrices B et A. La matrice C=B.A représente dès lors la composition gOf, et elle est de dimension pÃn, ce qui correspond à une application VnâZp. Le produit matriciel n'est pas commutatif, et l'ordre de multiplication B.A reflète l'ordre de la composition gOf. La composition d'applications linéaires est associative, tout comme le produit matriciel : (hOg)Of=hO(gOf) et (C.B).A=C.(B.A). Rang d'une matrice.
Noyau.
Image.
Lien
entre noyau, image et dimension.
dim(im(A)) + dim(ker(A)) = dim(dom(A)), soit : rang(A)+null (A) = n. où n est le nombre de colonnes de la matrice A (dimension de l'espace de départ). Cela signifie que la somme des dimensions de l'image (rang) et du noyau (nullité) est égale au nombre total de variables dans le système. Le rang d'une matrice est égal au rang de sa transposée : rang(A) = rang(AT). Le rang d'une matrice est au plus égal au minimum de son nombre de lignes et de son nombre de colonnes. Trace
d'une matrice.
où aii sont les éléments diagonaux de A. Propriétés de la trace : ⢠Linéarité : tr(A+B)=tr(A)+tr(B); tr(cA) = c.tr(A), pour un scalaire c.Opérations élémentaires. On appelle opérations élémentaires (sur les lignes) d'une matrice des manipulations utilisées pour simplifier une matrice tout en préservant son contenu mathématique essentiel. Ce sont principalement : l'échange (permutation) de deux lignes, la multiplication d'une ligne par un scalaire non nul, l'ajout (ou la soustraction) d'un multiple d'une ligne à une autre et l'ajout tous les éléments d'une ligne à une autre ligne. Ces opérations préservent notamment le rang, la trace, le noyau et l'image d'une matrice. Augmentation d'une matrice L'augmentation d'une matrice est l'opération consistant à ajouter une ou plusieurs colonnes (ou éventuellement des lignes) à une matrice existante pour former une nouvelle matrice étendue, appelée matrice augmentée : une matrice A de coefficients et une matrice de constantes B. La matrice augmentée pourra se noter [A | B] ou (A |B). La matrice augmentée (A | B) a les propriétés suivantes : elle a le même nombre de lignes que la matrice A; elle a un nombre de colonnes égal au nombre de colonnes de A plus le nombre de colonnes de B; les éléments de la matrice A sont conservés dans la matrice augmentée; la colonne de constantes B est ajoutée à la fin de la matrice A. Contrairement à ce qui se passe avec les opérations élémentaires vues précédemment, l'augmentation d'une matrice transforme les propriétés de base de la matrice de départ. C'est une technique utile pour intégrer des informations supplémentaires dans une matrice, notamment pour la résolution de systèmes d'équations linéaires ou l'analyse de la dépendance linéaire entre les vecteurs ou les lignes d'une matrice, par exemple. Matrice de changement
de base. Matrice de passage.
Si un vecteur v est exprimé dans une base B1 et que l'on veut exprimer ce même vecteur dans une autre base B2â, une matrice de passage PB1âB2 permet de faire cette conversion. Elle satisfait la relation : [v]B2=PB1âB2.[v]B1 , où [v]B1ââ sont les coordonnées du vecteur v dans la base B1â, [v]B2ââ sont les coordonnées du vecteur v dans la base B2â, PB1âB2ââ est la matrice de passage de la base B1à la base B2â. Pour construire la matrice de passage PB1âB2â, on exprime les vecteurs de la base B2â dans la base B1., c'est-à -dire que l'on prend chaque vecteur de la base B2â et on les exprime comme une comme une combinaison linéaire des vecteurs de B1â. Les colonnes de PB1âB2ââ sont alors les coordonnées des vecteurs de B2â dans B1â. DéterminantsDéfinition.Le déterminant est une fonction qui associe à une matrice carrée un nombre réel ou complexe (selon le corps de définition de la matrice). Ce nombre (auquel on donne aussi le nom de déterminant par abus de langage), noté detâ¡(A) ou |A|, est un invariant fondamental qui contient des informations clés sur les propriétés de la matrice. Le calcul d'un déterminant d'une matrice carrée repose sur la somme alternée des produits des éléments de la matrice, pris selon des permutations de ses colonnes ou lignes, affectés de signes positifs ou négatifs selon la parité de la permutation. Pour une matrice 2x2, c'est simplement le produit des éléments de la diagonale principale moins le produit des éléments de l'autre diagonale. Pour des matrices plus grandes, on utilise souvent le développement par rapport à une ligne ou une colonne, réduisant ainsi le calcul à des déterminants de sous-matrices plus petites. Exemples
de déterminants faciles à calculer.
⢠Pour une matrice 2Ã2 :Propriétés élémentaires des déterminants. Déterminant de la matrice identité. Inâ étant la matrice identité de taille nÃn, on a detâ¡(In) = 1. Multiplication
des déterminants.
Déterminant
d'une transposée.
Ãchange
de lignes ou de colonne.
Linéarité
par rapport à une ligne ou une colonne.
Lignes
ou colonnes identiques.
Ligne
ou colonne nulle.
Multiplication
d'une ligne ou d'une colonne par un scalaire.
Facteur
commun dans une ligne ou colonne.
Inversion d'une
matrice.
Dans le cas d'une matrice carrée; l'existence du matrice inverse dépend de la valeur du déterminant de la matrice considérée : une matrice carrée A est inversible si et seulement si son déterminant est non nul : detâ¡(A) â 0. (Si detâ¡(A) = 0, on dit que la matrice alors la matrice est singulière; elle n'a pas d'inverse). Si A est inversible, alors : detâ¡(Aâ1)=1/detâ¡(A). Cas d'une matrice 2 x 2 : Inversion d'une matrice par la méthode de Gauss Jordan. La méthode de Gauss-Jordan est une technique numérique utilisée pour inverser une matrice carrée en mettant en oeuvre des opérations élémentaires sur les lignes. Elle est efficace pour inverser des matrices carrées, mais elle peut être coûteuse en termes de calculs pour des matrices de grande taille. Il existe d'autres méthodes plus efficaces pour inverser des matrices. Ãtapes de la méthode de Gauss-Jordan : 1) Création de la matrice augmentée . - On crée une matrice augmentée en ajoutant la matrice identité de même taille à la droite de la matrice d'origine.Condition d'indépendance linéaire de vecteurs. Le déterminant peut être utilisé comme critère pour vérifier l'indépendance linéaire d'un ensemble de vecteurs dans un espace vectoriel Un ensemble de vecteurs {v1, v2,â¦, vn} dans un espace vectoriel de dimension n est dit linéairement indépendant si l'équation c1âv1â + c2âv2â +â¯+ cnâvnâ = 0 n'admet comme solution que c1 = c2 = ... = cn = 0. Autrement dit, aucun vecteur de cet ensemble ne peut être exprimé comme une combinaison linéaire des autres. Si les vecteurs v1, v2,â¦, vnâ sont représentés par les colonnes d'une matrice carrée A de dimension nÃn, alors les vecteurs sont linéairement indépendants si et seulement si detâ¡(A)â 0. (Si detâ¡(A)=0, les vecteurs sont linéairement dépendants). Cela vient de ce
que le déterminant de la matrice A est un indicateur de l'inversibilité
de cette matrice. Si detâ¡(A)â 0, la matrice est inversible, ce qui signifie
que ses colonnes (ou ses lignes) forment une base de Systèmes d'équations LinéairesIntroduction aux systèmes linéaires.Un système d'équations linéaires est un ensemble d' équations linéaires qui doivent être satisfaites simultanément. Chaque équation linéaire est une équation de la forme : am1x + am2y + ... + amnz = b, où am1, am2, ..., an sont les coefficients constants de la m-ième éqation du système, x, y, ..., z sont des variables, et b est une constante. Théorème
de Rouché-Capelli.
Systèmes homogènes et non homogènes. Les systèmes d'équations linéaires peuvent être classés en deux catégories : les systèmes homogènes et les systèmes non homogènes. ⢠Systèmes d'équations linéaires homogènes. - Un système d'équations linéaires homogène est un système où toutes les équations ont une forme similaire, avec des coefficients constants et des variables, mais sans termes constants. En d'autres termes, toutes les équations ont la forme : a1x + a2y + ... + anz = 0, où a1, a2, ..., an sont des coefficients constants, x, y, ..., z sont des variables. Les systèmes homogènes ont les propriétés suivantes : ils ont toujours au moins une solution, qui est la solution nulle (x = y = z = 0); s'ils ont une solution non nulle, alors ils ont une infinité de solutions; les solutions sont des combinaisons linéaires des solutions fondamentales. ⢠Systèmes d'équations linéaires non homogènes. - Un système d'équations linéaires non homogène est un système où au moins une équation a un terme constant non nul. En d'autres termes, au moins une équation a la forme : a1x + a2y + ... + anz = b, où a1, a2, ..., an sont des coefficients constants, x, y, ..., z sont des variables, et b est un terme constant non nul. Les systèmes non homogènes ont les propriétés suivantes : ils peuvent avoir une solution unique, une infinité de solutions, ou aucune solution. Les solutions ne sont pas nécessairement des combinaisons linéaires des solutions fondamentales.Les systèmes homogènes et non homogènes peuvent être résolus à l'aide de méthodes similaires, telles que la méthode de Gauss, la méthode de Cramer, etc. Cependant, les systèmes homogènes sont souvent plus faciles à résoudre, car ils ont toujours une solution nulle et les solutions non nulles sont des combinaisons linéaires des solutions fondamentales. En revanche, les systèmes non homogènes peuvent être plus difficiles à résoudre, car ils peuvent avoir des solutions uniques ou infinies, et les solutions ne sont pas nécessairement des combinaisons linéaires des solutions fondamentales. Un système d'équations linéaires peut être représenté de plusieurs manières. La plus évidente est l'écriture l'une à la suite des autres (ou plutôt les unes sous les autres) :
Il peut être aussi représenté de manière compacte sous forme matricielle. La matrice A des coefficients, multipliée par le vecteur colonne X des inconnues, est égale au vecteur colonne B des termes constants : A.X = B. La résolution de ce système se ramène alors à des opérations matricielles. Méthodes de résolution.
Méthode
par substitution.
1) Isoler une variable dans l'une des équations.Méthode par combinaison linéaire (ou addition). la méthode par combinaison linéaire consiste à additionner ou soustraire les équations pour éliminer une variable. Ãtapes : 1) Multiplier les équations pour que les coefficients d'une variable soient opposés.Méthode matricielle (ou méthode de Gauss). Cette méthode utilise les matrices pour résoudre le système. Ãtapes : 1) Représenter le système sous forme matricielle A.X = B, où A est la matrice des coefficients, X le vecteur des inconnues, et B le vecteur des constantes.Méthode de Cramer. Cette méthode est applicable si le système a autant d'équations que de variables et si le déterminant de la matrice des coefficients n'est pas nul. Ãtapes : 1) Ãcrire le système d'équations linéaires sous la forme d'une matrice d'équations : Ax = b, où A est la matrice des coefficients, x est la matrice des inconnues et b est la matrice des constantes.La méthode de Cramer est facile à mettre en Åuvre avec des outils de calcul numérique. Cependant, elle nécessite de calculer plusieurs déterminants, ce qui peut être coûteux en temps de calcul pour les grands systèmes. Elle n'est pas adaptée pour les systèmes d'équations linéaires avec des coefficients non numériques. Méthodes
itératives (Jacobi ou Gauss-Seidel).
Jacobi : Chaque variable est calculée en fonction des valeurs des autres à l'itération précédente.Ces méthodes convergent sous certaines conditions, par exemple si la matrice des coefficients est strictement diagonale dominante Valeurs propres et vecteurs propresLes valeurs propres et les vecteurs propres d'une matrice révèlent des informations sur la transformation linéaire représentée par cette matrice. Les vecteurs propres sont des vecteurs qui sont seulement mis à l'échelle (multipliés par une constante, la valeur propre) par la transformation.Une valeur propre d'une matrice carrée A est un scalaire tel que l'équation suivante est satisfaite : Av=λv, où A est une matrice carrée nÃn, λ est une valeur propre, et v est un vecteur propre non nul. Un vecteur propre d'une matrice carrée A est un vecteur non nul qui, lorsqu'il est multiplié par la matrice A, donne un vecteur colinéaire à lui-même, multiplié par la valeur propre correspondante λ. Le vecteurs propres représentent des directions invariantes sous l'effet de la transformation linéaire définie par A. Si v est un vecteur propre, l'application de A ne change que sa magnitude (par λ) mais pas sa direction. Les valeurs propres indiquent les facteurs par lesquels les vecteurs propres sont dilatés ou contractés lors de la transformation. Pour trouver les valeurs propres et les vecteurs propres d'une matrice carrée, on suit les étapes suivantes : 1) Ãquation caractéristique : l'équation Av = λv peut être réécrite sous la forme : (AâλI)v=0, où I est la matrice identité. Pour qu'il existe une solution non triviale (v â 0) le déterminant de la matrice (AâλI) doit être nul : detâ¡(AâλI) = 0. Cette équation est appelée équation caractéristique. En la résolvant, on trouve les valeurs propres λ. Espaces euclidiensUn espace euclidien est un espace vectoriel réel de dimension finie muni d'une opération interne particulière appelée produit scalaire qui définit une norme (ou longueur) sur les vecteurs. Les espaces euclidiens sont souvent définis sur le corps des nombres réelsLe produit scalaire. Définition. Le produit scalaire (noté . ou â¹ , âº) est une opération qui donne un nombre à partir de deux vecteurs. Le produit scalaire entre deux vecteurs u = (u1, u2, â¦, un) et v = ( v1, v2, â¦, vn) dans un espace vectoriel réel 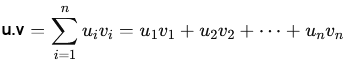 En termes matriciels, le produit scalaire de deux vecteurs u et v, correspond au produit matriciel de la transposée de u par v : 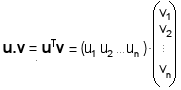 Propriétés du produit scalaire. Le produit scalaire est commutatif (u .v = v . u), linéaire par rapport à chaque vecteur (u . (k.v) = k.(u.v), (u + v). w = u.w + v.w), et positif défini (u.u ⥠0, et u.u = 0 si et seulement si u = 0). Norme, distance
et angle.
||u|| = â(u.u) = â(u1² + u2² + ... + un²) Pour tous les vecteurs d'un espace euclidien, on a vérifie : ⢠La positivité : ||u|| ⥠0, avec ||u|| = 0 si et seulement si u = 0.Distance entre deux vecteurs. La distance entre u et v dans Angle
entre deux vecteurs.
||u|| et ||v|| représentent les normes de u et v. Orthogonalité
Projection
orthogonale :
Base
orthonormale.
une base (b1,
b2,â¦,
bn)
de 1) bi.bj =0 pour i â j (orthogonalité)Dans une base orthonormale, les coordonnées d'un vecteur u sont simplement données par les produits scalaires des vecteurs de la base : 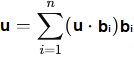 Produit vectoriel
.
Soient deux vecteurs
a et b dans Le produit vectoriel aÃb est défini par : 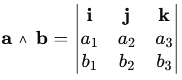 Où i, j, k sont les vecteurs unitaires selon les axes x, y et z. Le déterminant donne : aÃb=(a2b3âa3b2)iâ(a1b3âa3b1)j+(a1b2âa2b1)k Le résultat aÃb est orthogonal à a et b. La direction de aÃb est déterminée par la règle de la main droite : si les doigts de la main droite suivent a vers b, le pouce pointe dans la direction de aÃb. La norme du produit vectoriel est donnée par : ||aÃb|| = ||a||.||b||.sinâ¡Î¸, où θ est l'angle entre a et b. Le produit vectoriel est antisymétrique : aÃb = â(bÃa) Le produit vectoriel est nul aÃb = 0 ) si et seulement si a//b Propriétés
et identités remarquables du produit vectoriel.
Formule de Gibbs
(produit mixte avec produits vectoriel et scalaire). - Pour trois vecteurs
u,
v,
w
de Identité de Jacobi (double produit vectoriel). - L'identité de Jacobi décrit le comportement du double produit vectoriel : u ⧠(v ⧠w) = (u.w)v - (u.v)w. Cette identité est particulièrement utile dans la mécanique classique et la théorie des champs. Identité de Lagrange. - Pour deux vecteurs u et v, l'identité de Lagrange donne une relation entre les normes et les produits vectoriel et scalaire : ||u ⧠v||² = ||u||².||v||² - (u.v)². Cela exprime que le carré de la norme du produit vectoriel correspond au déterminant du produit mixte des vecteur s. Identité du triple produit mixte. - Pour trois vecteurs u, v, w, le produit mixte satisfait l'identité suivante : u. (v ⧠w) = v.(w ⧠u) = w. (u ⧠v). Cette égalité montre la cyclicité dans l'expression du produit mixte. Exemples d'applications
linéaires courantes dans R2.
x' = xcosâ¡Î¸âysinâ¡Î¸ et y' xsinâ¡Î¸+ycosâ¡Î¸, soit w = (xcosâ¡Î¸âysinâ¡Î¸, xsinâ¡Î¸+ycosâ¡Î¸), où θ est l'angle de rotation. La matrice de rotation correspondante est donnée par : 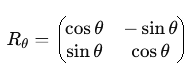 En dimension supérieure
( Changement
d'échelle (homothétie).
Pour un changement d'échelle anisotrope, les facteurs d'échelle peuvent être différents dans chaque direction : 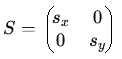 Une projection orthogonale sur une droite dans
Réflexion.
Formes linéaires, bilinéaires et quadratiquesFormes linéaires.Une forme linéaire est une application linéaire d'un espace vectoriel V (sur un corps K, souvent R ou C) vers le corps K. Si f : VâK est une forme linéaire, alors pour tous x,y Le noyau kerâ¡(f)={x Dans V=Rn, une forme linéaire peut être écrite comme : f(x) = a1âx1â + a2âx2â +â¯+ anâxnâ = â¨a,xâ©où a=(a1,â¦, an) Formes bilinéaires.
B(x+y, z) = B(x,z) + B(y,z) (linéarité par rapport à la première variable),
On dit qu'une forme bilinéaire est symétrique si B(x,y) = B(y,x); elle est antisymétrique si B(x,y) = âB(y,x). La matrice associée A dépend de la base choisie dans V. Le produit scalaire est une forme bilinéaire symétrique et définie positive. Formes quadratiques.
Les formes quadratiques ont des propriétés telles que : ⢠Homogénéité : La forme quadratique est homogène, c'est-à -dire que pour tous les vecteurs u et pour tous les scalaires a, on a : Q(au) = a2 Q(u)Les formes quadratiques peuvent être : ⢠Définies positives : Si Q(u) > 0 pour tous les vecteurs u non nuls.Le rang d'une forme quadratique est le nombre de valeurs propres non nulles de sa matrice. Le défaut d'une forme quadratique est le nombre de valeurs propres nulles. Le rang et le défaut sont liés à la nature de la forme quadratique (définie positive, définie négative ou indéfinie). La signature d'une forme quadratique est le nombre de valeurs propres positives moins le nombre de valeurs propres négatives. Elle est liée à la nature de la forme quadratique (définie positive, définie négative ou indéfinie). La forme quadratique euclidienne est une forme quadratique définie positive qui correspond à la longueur d'un vecteur. La forme quadratique de Lorentz est une forme quadratique qui correspond à la métrique de l'espace-temps en relativité restreinte. |
| . |
|
|
|
|||||||||||||||||||||||||||||||
|