Les érudits arabes (ou, pour mieux dire, arabo-musulmans) ont ainsi maintenu un vif intérêt pour le travail des mathématiciens indiens pendant les siècles qui ont suivi et ont joué un rôle actif dans la préservation et la traduction de nombreux textes indiens. Les mathématiciens arabes leur doivent leur système de numération, leur trigonométrie, et aussi la forme  « rhétorique » de leur algèbre.

Dans un deuxième temps (vers le IX^e siècle), ils faisaient traduire les ouvrages grecs. Parmi ceux-là citons ceux d'Euclide, d'Archimède, d'Apollonius, de Héron, de Ptoléme, de Pappus, de Diophante. Leurs problématiques se sont vite fait une place dans les spéculations des mathématiciens arabes. Les Ecoles Arabes continuèrent à prospérer jusqu'au XV^e siècle 

Les travaux des Arabes (en y comprenant ceux des auteurs qui écrivirent en Arabie et qui vivaient sous la domination des Musulmans d'Orient) en arithmétique, en algèbre et en trigonométrie, dénotent une très grande supériorité. Ils surent comprendre l'importance de la géométrie et de ses applications à l'astronomie, mais ne reculèrent pas de façon importante les bornes de cette science. On peut aussi ajouter qu'ils ne firent aucun progrès notable en statique, en optique ou en hydrostatique, bien qu'il soit hors de doute qu'ils aient eu une connaissance complète de l'hydraulique pratique.

Même lorsque les méthodes algébriques des Arabes sont presque générales, les applications qu'ils en donnent roulent dans tous les cas, sur des problèmes numériques, et l'algèbre est tellement confondue avec l'arithmétique qu'il est difficile d'isoler les deux sujets. D'après leurs traités d'arithmétique et les observations que l'on trouve disséminées dans divers ouvrages d'algèbre, nous pouvons dire que les méthodes qu'ils employèrent pour effectuer les quatre opérations fondamentales étaient analogues à celles actuellement en usage; mais les problèmes qui servaient d'application étaient identiques à ceux que l'on trouve dans les livres modernes et résolus par des méthodes semblables, telle la règle de trois. Quelques légers perfectionnements furent introduits dans la notation, comme par exemple un trait pour séparer dans une fraction le numérateur du dénominateur; de là vient l'emploi de la ligne placée entre deux symboles pour indiquer la division. 

Connaissances mathématiques de sources grecques.
Les Arabes ont puisé leurs premières connaissances scientifiques chez les médecins grecs qui soignèrent les Califes à Bagdad. On raconte que lorsque les conquérants Arabes établirent leurs résidences dans les villes ils éprouvèrent des maladies qui leur avaient été complètement inconnues quand ils habitaient le désert. L'étude de la médecine était à cette époque entre les mains des Grecs et des Juifs, et plusieurs d'entre eux, encouragés par les Califes, s'établirent à Bagdad, à Damas et dans d'autres villes; leurs connaissances scientifiques étaient bien plus étendues et plus exactes que celles des Arabes, et l'instruction de la jeunesse ne tarda pas à leur être confiée.

L'introduction de la science antique était rendue d'autant plus facile que plusieurs petites écoles grecques existaient dans les contrées soumises aux Arabes : il y en avait une depuis plusieurs années à Edesse, au milieu des chrétiens Nestoriens et d'autres encore à Antioche, Emesse et même à Damas, qui avaient conservé les traditions et quelques uns des résultats de l'enseignement grec.

Les Arabes remarquèrent bientôt que les Grecs tiraient leurs connaissances médicales des ouvrages d'Hippocrate, d'Aristote et de Galien, et ces livres furent traduits en arabe, vers l'année 800, sur l'ordre du Calife Hâroûn er-Rachîd. Cette traduction excita tellement l'intérêt que son successeur Al-Mamoun (813-833) envoya à Constantinople et en Inde, des commissions chargées de prendre des copies du plus grand nombre possible d'ouvrages scientifiques.

Il engagea en même temps un nombreux personnel de clercs syriens pour traduire ces livres en Arabe et en Syriaque. Afin de désarmer le fanatisme, ces clercs furent d'abord appelés les docteurs du Calife, mais en 851 ils formèrent une académie et le Calife Mutawakkel (847-861) en donna la direction au plus célèbre d'entre eux, Honein ibn Ishak. Ce dernier et son fils Ishak ibn Honein révisèrent les traductions avant de les livrer à la publicité. Ils ne connaissaient ni l'un ni l'autre, les mathématiques, et de ce fait plusieurs erreurs se glissèrent dans leurs écrits, mais un autre membre de l'académie, Thabit ibn-Qurrah (V. plus bas) fit paraître peu, après, de nouvelles éditions qui devinrent par la suite les textes officiels.

Les Arabes possédèrent ainsi, avant la fin du IX^e siècle, des traductions des oeuvres d'Euclide, d'Archimède, d'Appollonius, de Ptolémée et de plusieurs autres : quelques uns de ces ouvrages ne nous sont parvenus que par leurs traductions arabes.
Un fait curieux et qui montre dans quel oubli était tombé Diophante, c'est que autant que nous pouvons le savoir, les Arabes n'eurent connaissance de son grand ouvrage que 150 ans plus tard, alors qu'ils s'étaient déjà familiarisés avec la notation et les procédés de l'algèbre.

Connaissances mathématiques de sources indiennes
Les Arabes faisaient un commerce considérable avec le monde indien, et sous le califat de  Abou Djafar al-Manzor (754-775) ils avaient eu connaissance de l'un ou des deux grands ouvrages originaux des Indiens sur l'Algèbre, mais ils n'y prêtèrent une sérieuse attention que 50 ou 60 ans plus tard. L'algèbre et l'arithmétique des Arabes furent en grande partie basées sur ces traités.

Les ouvrages dont les Arabes eurent tout d'abord connaissance furent ceux d'Aryabhata et de Brahmagupta, et peut-être ceux de leurs successeurs Sridhara et Padmanabha; il est douteux qu'ils aient jamais fait beaucoup usage du grand traité de Bhaskara. Il est probable que l'attention des Arabes se porta sur les ouvrages des deux premiers de ces auteurs, parce qu'ayant adopté les méthodes arithmétiques des Indiens, il leur était possible d'étudier les livres mathématiques de ces savants. 

Les Arabes avaient toujours fait un commerce considérable avec les Indes, commerce qui naturellement prit une plus grande extension avec l'établissement de leur empire ; à cette époque, vers l'an 700, ils trouvèrent chez les marchands indiens, le système de numération avec lequel nous sommes familiarisés, et que ces derniers commençaient à employer; ils l'adoptèrent aussitôt. Il leur était d'autant plus aisé d'utiliser immédiatement ce système qu'ils ne possédaient aucun ouvrage scientifique ou littéraire leur en donnant un autre; il est même douteux que celui dont ils faisaient alors usage, fut autre que le système le plus primitif de notation pour représenter les nombres. 

Les Arabes (de même que les Indiens) paraissent n'avoir fait que peu d'usage de l'abaque, si même ils l'ont connu, et par suite, ils doivent avoir trouvé les méthodes de calcul des Grecs et des Romains extrêmement laborieuses. La date la plus ancienne assignée pour l'emploi, en Arabie, du système de numération décimale est 773. C'est à cette époque que quelques tables astronomiques indiennes furent apportées à Bagdad, et il est à peu près certain qu'elles comportaient l'usage des symboles numériques indiens (y compris le zéro).

L'apogée des mathématiques arabes.
On place l'apogée des mathématiques arabes entre le IX^e et le XI^e siècles. Et l'on peut mentionner pendant cette période les nom suivants :

Al-Khwârizmî.
Abou-'Abdallah al-Kwhârizmî, natif du Khorassan, bibliothécaire du calife Al-Mammoun, voyagea en Inde. A son retour, il écrivit une Algèbre intitulée Al-gebr we'l mukabala (Eléments d'algèbre) d'après celle de Brahmagupta, mais dans laquelle quelques-unes des démonstrations sont exposées suivant la méthode grecque, c'est-à-dire en représentant les nombres par des lignes.

Le mot arabe al-gebr (de gabar = rétablir), d'où est dérivé le mot algèbre, peut être traduit par La restitution et se rapporte à ce fait que l'on peut augmenter ou diminuer d'une même quantité les deux membres d'une équation (autrement dit :  compléter une négation, c'est-à-dire le transport d'un terme négatif d'un membre de l'équation dans l'autre membre; ); al-mukabala (= opposition, confrontation) signifie le procédé de simplification, et est généralement employé pour désigner la réduction des termes semblables en un seul.

L'algèbre de Khwârizmî tient une place importante dans l'histoire des mathématiques, car nous pouvons dire que les ouvrages arabes et ceux des premières années de la Renaissance, qui parurent dans la suite, s'en inspirèrent directement. C'est grâce à lui que Léonard de Pise, qui avait été s'instruire près des Arabes, put, en le traduisant, doter l'Europe de cette branche des mathématiques. Cette algèbre, considérée comme élémentaire par un savant de Bagdad du XI^e siècle, devint le vade-mecum des Occidentaux sept cents ans après, et servit de base à leurs études scientifiques jusqu'à Viète. C'est ainsi aussi que par cet ouvrage le système de numération décimale Arabe ou Indien pénétra en Occident. Comme c'était le premier livre offrant un pareil système de notation, l'arithmétique qu'il présentait reçut le nom d'Algorisme ou Algorithme, c'est-à-dire l'art d'Al-khwârizmi,  pour la distinguer de celle de Boëce. Cette appellation demeura en usage jusqu'au XVIII^e siècle.

L'Algèbre de Khwârizmî traite de l'addition, de la soustraction et de la multiplication des expressions qui contiennent la quantité inconnue, ou son carré ou sa racine carrée. L'inconnue y est appelée s'aï, c'est-à-dire chose, res, ou encore gidr, racine, radia : le mot gidr dérive de gadr, qui signifie la racine d'une plante. C'est donc aux Arabes que l'on doit le nom de racine, que les Grecs désignaient par le mot côté, pleura (d'un carré). Comme les Indiens, il emploie des considérations géométriques afin d'affirmer la certitude des opérations. Sa méthode lui sert ensuite à résoudre l'équation du second degré.

L'ouvrage comprend cinq parties. 

• Dans la première, Khwârizmî donne sans aucune démonstration, des règles pour la résolution des équations du second degré qu'il divise en six classes correspondant aux formes :

ax² = bx, ax² = c, bx = c, ax² +bx = c, ax² + c = bx et ax² = bx + c

Cependant le livre de Khwârizmî, sur ces questions, est moins complet que les traités indiens. Ainsi il ne parle pas des équations indéterminées du second ni du premier degré, mais l'auteur a soin de nous prévenir que c'est un simple résumé destiné à faciliter les opérations les plus usuelles, et non un cours complet comme les Arabes en possédaient déjà.

• Il donne ensuite des démonstrations géométriques de ces règles en opérant comme dans la proposition 4 du livre II d'Euclide. Pour résoudre l'équation x² + 10x = 39, par exemple, ou une équation quelconque de la forme x² + px = q, il donne deux méthodes et nous allons en exposer une, basée sur la figure suivante :
-

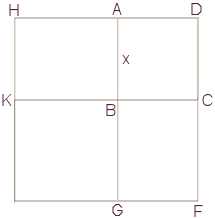Supposons que AB représente la valeur de x et construisons sur cette droite le carré ABCD. Prolongeons DA jusqu'en H et DC jusqu'en F, de sorte que AH = CF = 5 (ou 1/2 p), et complétons le carré. Alors les aires AC, HB et BF représentent les quantités x², 5x et 5x. Par suite le premier membre de l'équation est représenté par la somme des aires AC, BH et BF. Ajoutons aux deux membres de l'équation le carré KG dont l'aire est 25 (ou 1/4 p² ) ; nous obtenons un nouveau carré dont l'aire est, par hypothèse, égale à 39 + 25 c'est-à-dire à 64 (ou q+1/4 p²) et dont le côté est par conséquent 8. Le côté de ce carré DH qui est égal à 8 surpasse AH qui vaut 5 de la valeur de la quantité inconnue qui est dès lors égale à 8 - 5 ou 3.

• Dans la troisième partie du livre, Khwârizmî considère le produit de (x± a) par (x ± b). 

• Dans la quatrième partie, il établit les règles pour l'addition et la soustraction d'expressions comprenant l'inconnue, son carré ou sa racine carrée; il donne des règles pour le calcul des racines carrées, et termine par les théorèmes exprimés par les formules : .

• Dans la cinquième et dernière partie, il donne quelques problèmes dont voici un exemple : trouver deux nombres dont la somme est égale à 10 et dont la différence des carrés est 40.

Les Banu Musa.
Les trois frères Banu Musa ( = les fils de Musa bin Shakir, un astronome de bagdad originaire du Khorasan), contemporains Khwârizmî, se montrèrent de remarquables mathématiciens. Mohammed, le plus célèbre des trois, exécuta une des premières opérations géodésiques exactes. Il mesura un degré de méridien dans la plaine de Sindjar. Il calcula aussi des tables astronomiques, et composa un Traité des mouvements célestes assez curieux. Ahmed écrivit sur Les Machines, et Hasen s'occupa de la Trisection de l'angle. Enfin les trois frères composèrent ensemble une Géométrie où se rencontre la démonstration de la formule exprimant la surface d'un triangle en fonction des trois côtés.

Chargés d'une mission en Asie Mineure, en Perse, en Égypte et en Grèce, afin d'y recueillir les meilleurs manuscrits scientifigues, Ahmed et Hasen rencontrèrent à Harran en Mésopotamie; un astronome de talent, Thabit ibn Qurra, qu'ils emmenèrent avec eux à Bagdad. 

Thabit ibn-Qurrah.
Thabit ibn-Qurrah (mort en 900 de notre ère)  , qui paraît s'être le premier aperçu de la variabilité de l'obliquité de l'écliptique,  a publié des traductions des principaux ouvrages d'Euclide, d'Apollonius, d'Archimède et de Ptolémée  très estimées dans tout l'Orient. Il composa également plusieurs traités originaux qui sont tous perdus, à l'exception d'un fragment d'algèbre relatif aux équations du troisième degré qu'il résolvait à l'aide de la géométrie. Parmi ces ouvrages, il en est un qui avait pour titre, traduit en latin : de Problematibus algebricis geometricis ratione comprobandis. C'est sans doute le titre de cet ouvrage qui a fait dire à Montucla que

« [Thabit ibn-Qurra] a écrit sur la certitude du calcul algébrique, ce qui pourrait donner lieu de penser que les Arabes eurent aussi l'heureuse idée d'appliquer l'algèbre à la géométrie. »

« un art savant, qui traite des nombres absolus et des grandeurs d'une manière telle, que les quantités inconnues, étant jointes à une chose connue, peuvent être déterminées, la chose connue étant une quantité ou un rapport. »

Un autre de ses livres, sa dissertation sur les « nombres amiables », dont chacun est la somme des facteurs des autres, est une des premières découvertes originales des Arabes, et prouve que l'arithmétique de Pythagore n'y était pas délaissée.

El-Battânî.
El-Battânî, l'Albategnius des Latins (né à Baten en 877, mort à Bagdad en 929) , surnommé le Ptolémée Arabe, écrivit la Science des astres, qui parut en latin, avec le commentaire de Regiomontanus, à Bologne, en 153, et qui doit être mentionnée parce qu'elle contient la découverte du déplacement de l'apogée du Soleil. Il y fait aussi
 une innovation importante, dont on a voulu lui contester la priorité, en substituant les sinus aux cordes : les angles sont déterminés par la « demi-corde de l'arc double », c'est-à-dire par le sinus de l'angle (en prenant le rayon vecteur comme unité). Il divise, comme Ptolémée, le diamètre en 120 parties, conséquemment le rayon en 60 parties. Puis il détermine la corde de 120°, la corde du supplément d'un arc quelconque dont la corde est déjà connue, les cordes de 90°, de 36° et de 72°; enfin il emprunte à Ptolémée les théorèmes suivants :

« Si l'on a les cordes de deux arcs, on aura aussi celles de leur somme et de leur différence; - si l'on connaît la corde d'un arc, on aura aussi celle de sa moitié; - si les arcs sont petits, leurs cordes seront entre elles à très peu près comme les arcs. »

Mais dans l'exposition de ce qui suit, l'auteur arabe cesse de copier Ptolémée.

« Le diamètre EC qui divise, dit-il, en deux arcs égaux l'arc AB, divise pareillement la corde AB en deux parties égales, AD et DB, qui sont les moitiés de la corde de l'arc double AB. Or, la corde est au demi-diamètre (rayon) comme la demi-corde est au rayon. Ainsi, quand on a un arc AC, au lieu de le doubler pour en chercher la corde AB, on peut s'en tenir à l'arc simple AC et considérer la demicorde AD ou DB, qui sont de part et d'autre du diamètre. C'est de ces demi-cordes que nous entendons nous servir dans nos calculs, où il est bien inutile de doubler les arcs. Ptolémée ne se servait de cordes entières que pour la facilité des démonstrations; mais nous, nous avons pris ces moitiés des cordes des arcs doubles dans toute l'étendue du quart de cercle, et nous avons écrit ces demi-cordes directement à côté de chacun des arcs, depuis 0° jusqu'à 900, de demi-degré en demi-degré; ainsi, la moitié de la corde de 60° se trouve vis-à-vis de 30°; la moitié de la corde de 120° vis-à-vis de 60°, et la moitié de la corde de 180°, ou le rayon, vis-à-vis de l'arc de 90°, et ainsi des autres; en sorte que, quand nous parlerons de corde, il faudra entendre la demi-corde de l'arc doublé, à moins que le contraire ne soit expressément déclaré. »

La demi-corde de l'arc double est exprimée en arabe par le mot djib, qui signifie pli; c'est la corde pliée en deux, comme pourrait l'être le pli d'une robe, qui se dit sinus, en latin : c'est de là que vient, suivant quelques-uns, le mot de sinus, appliqué à la demi-corde. Mais d'autres le font venir de l'abréviation latine s. ins., pour semis inscripta, le mot inscripta étant le nom de la corde entière, et semis inscripta celui de la demi-corde.

El-Battâni était également en possession de la formule fondamentale de la trigonométrie sphérique donnant le côté d'un triangle en fonction des deux autres côtés et de l'angle compris.

Avicenne.
Avicenne (980-1037) n'est pas un mathématicien, mais on peut noter ici qu'il avait une règle pour vérifier l'exactitude des résultats de l'addition et de la multiplication : c'est la règle qui est enseignée dans nos traités d'arithmétique sous le nom de preuve par 9.

Abu Al-Wafa.
Abu Al-Wafa (940-998) qui travaillait à Bagdad, a écrit, suivant Aboul-Faradj, sur l'arithmétique de Diophante. Il a connu les formules des tangentes et des cotangentes, et même celles des sécantes et des cosécantes, dont aucun auteur n'avait encore parlé. Il a calculé seulement des tables de tangentes et cotangentes; il s'en est servi pour simplifier le calcul des formules connues, mais il n'a pas trouvé les formules qui manquaient encore à la trigonométrie des Grecs et des Arabes. Il était célèbre non seulement comme astronome - ayant découvert les variations lunaires - mais comme l'un des mathématiciens les plus remarquables de son temps.

Omar Khâyyam.
Omar Khayyâm (ca. 1017-1123), qui vivait à Nichapour en Perse est surtout connu comme poète. Mais il est aussi à citer comme mathématicien à cause de la façon dont il a traité géométriquement les équations du troisième degré : il obtenait une racine en déterminant l'abscisse du point d'intersection d'une conique et d'un cercle. Les équations qu'il a considérées sont des formes suivantes dans lesquelles a et c représentent des entiers positifs. x³ + b²x = b²c, dont la racine, dit-il, est l'abscisse du point d'intersection de x² = by et y² = x(c - x). x³ + ax² = b²c, dont la racine est l'abscisse du point d'intersection de xy = c², et y² = c(x + a). x³ ± ax² + b²x = b²c ayant pour racine l'abscisse du point d'intersection de y² = (x ± a) (c - x) et x(b ± y) = bc. 

Il donna une équation du quatrième degré, à savoir : (100 - x²) (10 - x)² = 8100, dont la racine est déterminée par le point d'intersection de (10 - x)y = 90 et x² + y3 =100.

On a prétendu aussi que Khâyyam avait affirmé l'impossibilité de résoudre en nombres entiers l'équation x³ + y³ = z³ ; en d'autres termes, il aurait su que la somme de deux cubes ne peut jamais être un cube. En admettant qu'il ait énoncé cette proposition, il est maintenant impossible de dire s'il en a donné une démonstration exacte, ou bien s'il l'a reconnue par une induction hardie, ce qui serait plus vraisemblable; mais le fait qu'un pareil théorème lui ait été attribué, montre les progrès extraordinaires accomplis en algèbre par les Arabes.

Al-Karkhi.
L'autre mathématicien de cette époque que nous avons mentionné fut Abu Bakr Muhammad ibn al-Hasan al-Karkhi (vers 1000), d'origine persane, maus qui vivait à Bagdad. Il donna les expressions des sommes des première, seconde et troisième puissances des n premiers nombres entiers; il résolut diverses équations dont quelques-unes de la forme ax²^p ± bx^p ± c = 0; et s'occupa des quantités irrationnelles montrant par exemple que .

Ibn al Haytham.
Hassan Ibn al-Haytham (987-1038), connu en Occident sous le nom de Alhazen, a publié un Traité des connues géométriques, aux environs de l'an 1010. Cet opuscule donne une idée assez exacte des considérations métaphysiques répandues chez les géomètres arabes. Des deux parties qui le composent, la première et la plus originale renferme des questions de lieux, la seconde comprend une suite de propositions dans le genre de celles traitées dans les Data d'Euclide. Elles sont cependant différentes de ces dernières et souvent assez difficiles. Pour en donner une idée, citons les deux suivantes :

• Quand on a un triangle dont les côtés et les angles sont déterminés, et qu'on mène une ligne du sommet à la base, si le rapport du carré de la droite au rectangle formé sur les deux segments de la base est connu, la ligne sera donnée de position.

• Lorsqu'on a deux cercles connus de grandeur et de position, et qu'on trace une droite tangente aux deux cercles, cette droite est déterminée en grandeur et en position.

Al-Sindjar.
Ahmed ben-Mohammed ben Abd al-Gehl, dit  Al-Sindjar (vers 1100), est auteur d'un traité sur les Sections coniques (conservé dans les manuscrits arabes de la Bibliothèque de Leyde) et de trois opuscules, contenus dans le manuscrit n° 1104 de la Bibliothèque nationale de Paris. Parmi ces  opuscules, l'un traite des Règles géométriques, un autre Des lignes menées d'un ou de plusieurs points donnés à des cercles donnés, et le troisième d'une Réponse à des questions proposées sur le livre des Lemmes d'Archimède

Les derniers mathématiciens arabo-musulmans.
A partir du XII^e siècle, la culture arabo-musulmane décline, en même temps que ces centres se déportent de l'Orient la Péninsule ibérique ou le Maroc. Entre le XII^e et le XV^e siècle, les mathématiciens arabes notables sont rares et leurs apports restent modestes. C'est à peine si on encore nommer Nasir al-Din qui vivait au XIII^e siècle, à l'époque de la domination mongole. Al-Din a traduit des mathématiciens grecs et a cru pouvoir donner une "démonstration" du postulat d'Euclide. D'autres auteurs s'intéressent à la formation des triangles rectangles en nombres entiers, notamment Abou-Djafar Mohammed Ibn- Al-Hoçaïn. Son traité (sur la Formation des triangles rectangles ayant les côtés rationnels) renferme une importante donnée historique. On y voit qu'Abou-Mohammed Al-Khodjandj avait déjà démontré que la somme de deux cubes n'est jamais un cube. Citons encore Jabir Ibn-Aflah, qui se consacre à la trigonométrie sphérique, Ibn-Khaldoun (1332-1406), qui fait le lien entre l'Orient et l'Occident, entre Le Caire et Fès, et s'est intéressé à l'arithmétique, à la sommation de séries de cubes, etc.,  et, plus intéressant peut-être, Ibn al-Bannaâ :

Ibn al-Bannâ, etc.
Dans un ouvrage intitulé leTalkhys, Ibn Al-Bannâ, qui professait, en 1222, les mathématiques et l'astronomie au Maroc, a exposé lui-même son objectif en ces termes :

 « Le but, dans la composition de ce traité, est d'analyser succinctement les opérations du calcul, d'en rendre plus accessibles les portes et les vestibules, et d'en établir solidement les fondements et la bâtisse. Il comprend deux parties, la première sur les opérations du nombre connu, la seconde sur les règles qui permettent d'arriver à connaître l'inconnue demandée, à l'aide des connues, s'il existe entre elles la liaison que cela exige. »