Au cours de ce trajet, les positions des étoiles par rapport au Soleil changent lentement, si bien que d'un jour sur l'autre, elles se lèvent avec quatre minutes de retard sur la veille. Et il faudra au total que la Terre ait accompli une révolution, c'est-à-dire une tour complet autour du Soleil pour que la sphère céleste retrouve une même orientation relative. La durée de cette révolution est d'environ 365 jours et pendant ce temps, la Terre parcourt environ 936 millions de kilomètres. La vitesse orbitale moyenne atteint donc environ 29 600 m/s, ou encore 106 700 km/h. Ce mouvement, qui est celui qui sera dit de translation ou de révolution, et qui obéit aux lois de Kepler, s'ajoute au mouvement de rotation qui est d'importance presque égale, mais sans lien de dépendance avec lui, car il n'affecte  pas la position dans l'espace de son centre de gravité. 

La Terre accomplit cette rotation sur elle-même autour de  son axe, en un jour. La vitesse de rotation est beaucoup moindre que celle du mouvement de translation. A l'équateur, elle est de 465 m/s. Et, surtout, l'axe de rotation ne coïncide pas avec la perpendiculaire à l'écliptique: il fait, avec cette, ligne un angle, sensiblement constant dans l'espace d'une année, de 23° 27'. Tel est aussi et par suite l'angle que forme le plan de l'équateur terrestre avec le plan de l'écliptique et qui constitue, ce qu'on appelle l' obliquité de I'écliptique. Celle-ci a une importance particulière, car la combinaison de cette inclinaison avec le mouvement annuel de translation, produit les saisons, un peu de la même façon que  le mouvement diurne de rotation, engendre la succession des jours (naturels) et des nuits. 
 

Le long de son parcours sur son orbite, l'angle entre l'axe de rotation de la Terre et la ligne qui la joint au Soleil sert à définir des points de la sphère céleste et des moments de l'année, et dont la date exacte varie d'une année sur l'autre du fait des décalages introduits par le calendrier Grégorien, et qui jouent un rôle spécial, puis qu'ils sont les carrefours à partir desquels sera définie la succession des saisons. Il s'agit des solstices et des équinoxes.

Les solstices*.
Les solstices ou points solsticiaux sont deux points de l'écliptique diamétralement opposés, qui correspondent aux époques, également appelées solstices, où le Soleil se trouve quand  les jours naturels et les nuits ont des longueurs extrêmes. Le nom de solstice vient de ce qu'à leur époque, le Soleil paraît, pendant plusieurs jours, se lever et se coucher aux mêmes points de l'horizon. A ces moments de l'année, qui se placent l'un le 21 ou 22 juin, et l'autre le 21 ou 22 décembre, le Soleil  l'axe de la Terre est inclus sur un plan qui est perpendiculaire à l'écliptique et passe par la Terre et le Soleil. L'axe qui joint les deux points solsticiaux est appelé ligne des solstices; il est perpendiculaire à la ligne des équinoxes.

Les équinoxes*.
Les équinoxes ou points équinoxiaux sont les deux points de l'écliptique, qui correspondent aux époques, également appelées équinoxes, où, comme le suggère l'étymologie, le jour naturel est égal à la nuit (Les Jours et les nuits). A ces moment de l'année, qui correspondent au 20 ou 21 mars et  au 22 ou 23 septembre, le Soleil se lève exactement à l'Est et se couche exactement à l'Ouest et l'axe de la Terre est inclus sur un plan tangent de son orbite. Le point équinoxial de mars est aussi appelé point vernal.  Il sert de base à la définition des systèmes de coordonnées écliptiques et célestes. Le passage du Soleil par ce point marque aussi dans l'hémisphère Nord le début du printemps. L'axe qui joint les deux points équinoxiaux est appelé ligne des équinoxes. 

L'année*
On appelle année (du latin annus) une certaine période de temps, approchant la durée de la révolution de la Terre autour du Soleil, et adoptée comme unité. Lorque l'année s'applique plus spécialement  à des phénomènes célestes cycliques, impliquant directement la révolution de la Terre autour du Soleil, elle est dite astronomique. Et lorsqu'elle elle s'applique aux usages sociaux, on parle d'année civile ou encore  - puisque c'est la période de temps considérée dans les calendriers, d'année calendaire -. Année astronomique et année civile sont susceptibles de définitions diverses, chacune pouvant leur conférer une durée différente.

Les années astronomiques
En astronomie, on se sert généralement du mot année pour désigner le temps employé par le Soleil pour parcourir l'écliptique et ramener les mêmes saisons. Entendue dans ce sens l'année prend le nom d'année tropique. Mais les astronomes définissent également d'autres intervalles de temps entre deux passages consécutifs du Soleil par un même point du ciel, et dont la durée pourra être légèrement différente selon le choix que l'on aura fait de ce point de référence : il existera ainsi, à côté de l'année tropique, une année sidérale, définie par rapport à la position des étoiles, une année anomalistique, qui sépare deux passages de la Terre à son périhélie, etc. 

L'année tropique (aussi appelée année solaire). - C'est la durée entre deux passages successifs au point vernal g, autrement dit l'intervalle entre deux équinoxes de printemps consécutifs. Elle vaut 365,24218967 jours solaires moyens (365 jours 5 heures 48 minutes. 45 secondes). Après cette période, les saisons se reproduisent exactement dans le même ordre. Dans cette évaluation on ne tient compte que de la précession solaire, mais non de la nutation, ce qui a pour effet de rendre l'année tropique tantôt un peu plus courte, tantôt un peu plus longue que ne l'indique le nombre que l'on vient de donner. Par l'effet de la précession, l'année tropique est un peu plus courte que l'année sidérale. Si au lieu d'exprimer la durée de l'année tropique en jours solaires moyens, on voulait l'exprimer en jours sidéraux, il faudrait ajouter un jour de plus. 

La durée de l'année tropique n'est exactement connue que depuis Hipparque; cet astronome détermina le moment précis des équinoxes, tandis qu'avant lui, on avait observé les solstices, dont le moment est très difficile à apprécier. L'année tropique est aujourd'hui de 11 s plus courte que de son temps. Ce changement est dû aux inégalités séculaires. Voici les valeurs diverses qui ont été attribuées à l'année tropique par divers astronomes au cours du temps :-

Auteur et référence	Année tropique
Copernic (1543)	365 j 5 h 49 mn 16 s
Tycho (Progymnasmes)	365 j 5 h 48 mn 45 s 5
Kepler (Tables rudolphines)	365 j 5 h 48 mn 57 s 6
Boulliaud (Astronomie phillolaïque)	365 j 5 h 49 mn 4 s 33
Riccioli (Almageste)	365 j 5 h 48 mn 40 s
Riccioli (Astronomie réformée)	365 j 5 h 48 mn 48 s
Flamsteed et Newton	365 j 5 h 48 mn 57 s 5
Le Monnier (Institut ast.)	365 j 5 h 48 mn 57 s
Halley (Tables astronomiques)	365 j 5 h 48 mn 54 s 8
Cassini (Tables astronomiques)	365 j 5 h 48 mn 52 s 4
Mayer (Mém. Göttingen)	365 j 5 h 48 mn 54 s
La Caille (Tables)	365 j 5 h 48 mn 49 s
Lalande	365 j 5 h 48 mn 48 s
Le Verrier (Ann. de l'obs. de Paris)	365 j 5 h 48 mn 47 s 51

L'année sidérale - c'est le temps employé par le Soleil pour revenir au méridien d'une même étoile, c'est-à-dire pour parcourir 360° sur son orbite. Elle vaut 365,256363051  jours solaires moyens (365 j 6 h 9 mn). Comptée en jours sidéraux, la même durée comprendrait un jour de plus. Cette période est plus longue que l'année tropique, en raison des mouvements de précession et de nutation : le point équinoxial ayant un mouvement annuel de 50"1 en sens inverse du mouvement du Soleil, cet astre revient au nouvel équinoxe avant d'avoir décrit l'arc de 360°. L'effet de la nutation est beaucoup moindre. 

L'année platonique (ou Grande Année). - Cette période correspond à la durée au bout de laquelle le décalage des pendules tropique et sidérale est remis à zéro.La précession des équinoxes induit en effet un cycle au bout duquel, la longitude des étoiles avançant chaque année de 50" environ, finit par avoir parcouru un cercle complet de 360°. C'est ce temps, estimé à  environ 25800 ans qui fixe la durée l'année platonique ou Grande année.

L'année anomalistique - On appelle ainsi, classiquement, le temps que la Terre emploie à retourner à son périhélie; c'est-à-dire, en termes géocentriques, le temps qui s'écoule depuis le moment où le Soleil est dans son apogée jusqu'à celui où il y arrive de nouveau, après une révolution entière. Ainsi, l'année anomalistique est de 365,259635864 jours, soit 365 jours 6 heures 15 minutes 20 secondes. Cette année est donc plus longue que l'année solaire de 26 minutes 35 secondes, parce qu'il faut ce temps-là au Soleil pour parcourir les 65 secondes et demie, dont son apogée avance chaque année.  De la même façon, cette période est également plus longue que l'année sidérale, car le périhélie possède un mouvement annuel de 44 s 76 dans le sens du mouvement du Soleil, de telle sorte que cet astre doit, pour atteindre le périgée, parcourir un arc supérieur à 360°. 

On ajoutera  définition de l'année, qui repose sur une logique différente. Elle est due à Gauss, qui avait proposé d'exprimer les distances  (La distance des astres) et le durées en fonctions des caractéristiques du Système solaire  : 

L'année gaussienne - C'est la période de révolution T =  365,2568983 jours, qui est donnée par la troisième loi de Kepler : a³/T² = G (M_S+M_T)/4p², où a est le demi-grand axe de la Terre, G, la constante de la gravitation, M_S la masse du Soleil et M_T celle de la Terre.

L'année grégorienne. Cette année, qui sert de base au  calendrier grégorien (du nom de la réforme élaborée par Lilius et Clavius, notamment, et instauré en 1582, par le pape Grégoire XIII) est aujourd'hui en usage dans la plupart des pays. Dans le calendrier grégorien, on donne à l'année en cours une longueur qui varie selon les règles suivantes :

1°) Première règle : une année ordinaire, ou commune, possède  365 jours, comme l'année vague de l'ancien calendrier égyptien; mais

2° Deuxième règle : lorsque le numéro de l'année est divisible par quatre (autrement dit tous les quatre ans), on intercale  un jour supplémentaire pour former ce qu'on appelle une année bissextile. Une année sur quatre a donc 366 jours, ce qui définit une année moyenne longue de 365,25 jours. Cette longueur était celle de l'année dite julienne, définie par Sosigène à l'instigation de Jules César en 46 av. J.-C., et que la réforme grégorienne justement a abolie. L'année astronomique tropique étant de 365,242216 jours, l'année julienne est trop longue. D'où :

3° Troisième règle : les années séculaires (1700, 1800, 1900, etc.) sont communes (on renonce à l'intercalation d'une année bissextile), sauf quand le nombre de siècles est divisible par quatre (1600 et 2000 ont été bissextiles). La moyenne des durées des années civiles sur cette période tombe alors à 365,2425 jours, ce qui fournit la durée de l'année grégorienne. 

C'est mieux que rien, mais ce n'est pas encore ça : sur une période de 3000 ans, le calendrier grégorien comptera un environ jour de trop...

Année solaire - Lorsqu'on rapporte la durée de l'année civile au mouvement du Soleil, on parle d'année solaire et de calendrier solaire. La plupart du temps - c'est le en particulier cas de l'année grégorienne -,  l'année astronomique dont on cherche à se rapprocher le plus est l'année tropique. Mais certains calendriers (au Sri Lanka et en Afrique, notamment) visent plutôt à définir une année proche de l'année sidérale. 

Année lunaire - Quand rapporte la durée de l'année au mouvement de la Lune et à la durée de l'année astronomique lunaire, on définit ce qu'on appellera une année civile  lunaire.  L'année astronomique lunaire est la succession de douze lunaisons valant chacune 29 j 12 h 44 m 2,8 s, c.-à-d. 354 jours 8 heures 48 mn 34 s. L'année civile lunaire lui répond est pour sa part composée tantôt de 12, tantôt de 13 mois ou lunaisons. Comme on le voit, cette définition n'est pas complètement indépendante de la définition de l'année solaire dont on cherche à se rapproche en multipliant par 12 ou par 13 la durée de la lunaison. Les années musulmanes sont essentiellement lunaires.

Année Luni-solaire - Quand les mouvements de la Lune et du Soleil sont tous les deux pris en compte et que leurs périodes respectives jouent à égalité dans la définition de l'année, celle-ci est dite luni-solaire. Comme une année lunaire de 12 lunaisons est  plus courte de 11 jours que l'année solaire, au bout de trois ans, il se trouve 33 jours de trop, dont on en prend 30, pour former un mois lunaire, que l'on ajoute à l'année, qui se trouve par là composée de 13 mois. Ce treizième mois ajouté est appelé mois embolismique. Les divers calendriers luni-solaires peuvent choisir des années et des rythmes très variables pour intercaler ce mois supplémentaire. Les années juives et plusieurs des anciennes années en usage en Grèce et en Inde se rangent dans cette catégorie.

De la même façon que la Grande année platonicienne (Platon) définit la période au bout de laquelle est corrigé le décalage entre le temps mesuré par l'année sidérale et celui mesuré par l'année tropique, on a imaginé différents cycles au bout desquels le cycle solaire finit par coïncider (ou du moins se rapprocher) du cycle lunaire. Parmi ces  approches, de natures et de motivations différentes, on mentionnera le cycle de Méton, le cycle dyonisien (ou de Victorius) et la Grande année d'Hipparque : 

Le cycle de Méton - la définition de cette période est due aux astronomes Méton et Euctémon qui, au Ve siècle av. J.-C., se rendirent célèbres en Grèce, en proposant, pour rétablir un ordre convenable dans les Fêtes grecques, un cycle fondé sur ce que, au bout de 19 années comprenant 235 lunaisons, les nouvelles Lunes reviennent, à peu près, aux mêmes dates de l'année. Ces fêtes étaient réglées d'après le premier jour de l'année, et ce jour était celui de la nouvelle Lune qui suit immédiatement le solstice d'été. Mais, à cause de l'insuffisance des connaissances astronomiques, l'époque du retour de ce jour n'était pas bien déterminée, et il s'ensuivait une confusion dans la célébration des fêtes grecques. La table résultant du nouveau cycle, exposée d'abord à Athènes par Méton, fut adoptée un siècle plus tard par presque toutes les villes et colonies grecques et inscrite en lettres d'or sur les monuments publics; de là vient le nom de nombre d'or donné au nombre qui, dans ce cycle, marque le rang de l'année.

Le cycle Dionysien - Les églises chrétiennes de l'Orient et de l'Occident s'étaient, dès leur origine, efforcées de mettre le retour de leurs fêtes en accord avec le ciel astronomique. Vers l'an 465 le pape Hilaire recourut ainsi aux lumières de Victorius d'Aquitaine pour introduire de l'ordre dans le calendrier. Combinant le cycle lunaire (cycle de Méton), de 19 ans, avec un cycle solaire, de 28 ans, Victorius imagina la période de 532 ans, qui est le produit de 19 par 28. Cette période devait avoir l'avantage de ramener la Lune de Pâques au même mois et au même jour de la semaine après 532 ans. Cela serait vrai si l'année était rigoureusement de 365 jours et 6 heures, et que le cycle de Méton fût exactement de 19 ans. Or cela n'est pas. L'invention n'en était pas moins ingénieuse, et elle aurait mérité de porter le nom de Victorius. Mais ce fut Denys (Dionysius) le Petit, abbé romain, qui lui donna le sien, par suite d'une correction qu'il y introduisit.

La Grande année d'Hipparque. Cette Grande année, dont l'invention est attribuée à Hipparque, est composée de 304 ans, dans l'espace desquels il y a 1760 mois lunaires synodiques presque exactement. Cette période est plus exacte que celle de Méton. 

Les saisons

On peut parler des saisons au sens astronomique et au sens météorologique. Dans le premier cas, elles renvoient à une manière de diviser l'année en tenant compte de la position relative de l'axe terrestre et du Soleil, dans le second, qui d'ailleurs est une conséquence du premier, on parlera de saisons pour rendre compte des conditions météorologiques globales qui règnent en un lieu particulier de la Terre, au fil de l'année.

Les saisons astronomiques.
En astronomie, on appelle saison le temps employé par le Soleil pour passer d'un équinoxe à un solstice ou d'un solstice à un équinoxe. L'année est partagée en quatre saisons : le printemps, qui va de l'équinoxe de printemps au solstice d'été; l'été, qui va du solstice d'été à l'équinoxe d'automne; l'automne, qui va de l'équinoxe d'automne au solstice d'hiver; l'hiver, qui va du solstice d'hiver à l'équinoxe de printemps. Ces dénominations ne sont pas, d'ailleurs, absolues. Pour dès raisons sur lesquelles nous reviendrons, elles s'appliquent inversement dans les deux hémisphères terrestres : tandis que notre hémisphère boréal est en été, l'hémisphère austral est en hiver, et réciproquement. De même pour le printemps et l'automne. Il est donc préférable, à l'instar des astronomes, de dire, si l'on veut éviter les confusions, équinoxe de mars, de septembre, solstice de juin, de décembre, au lieu des appellations habituelles d'équinoxe de printemps, d'automne, de solstice d'été, d'hiver, qui correspondent, suivant les lieux, à des époques différentes.

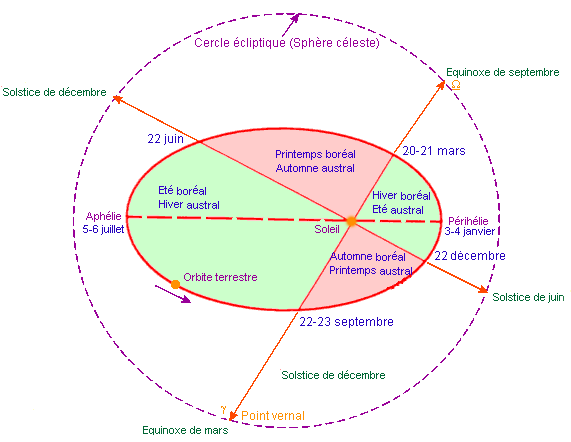
Saisons et position des solstices et des équinoxes sur la sphère céleste, 
rapportées aux positions de la Terre sur son orbite au cours d'une année.

Toutes les saisons n'ont pas la même durée. D'une part, en effet, l'orbite terrestre a, on le sait, la forme, non d'un cercle, mais d'une ellipse, dont le Soleil occupe un des foyers, et, comme conséquence de cette position excentrique du Soleil, notre planète a un plus long trajet à parcourir pour aller de l'équinoxe de septembre à l'équinoxe de mars que pour aller de l'équinoxe de mars à l'équinoxe de septembre. Sa vitesse est, en outre, plus grande de l'aphélie au périhélie, c.-à-d. de juillet à janvier, que du périhélie à l'aphélie, c.-à-d. de janvier à juillet. Enfin, le mouvement lent, mais incessant, du point vernal ou équinoxe de printemps et du périhélie l'un vers l'autre, détermine dans la durée des saisons une troisième cause de variation, qui influe, celle-là, non seulement sur la durée respective des quatre saisons, mais encore sur la durée de chacune, d'une année à l'autre. 

Actuellement, le printemps dure, en moyenne, 92 jours 21 heures, l'été 93 jours 14 heures, l'automne 89 jours 19 heures, l'hiver 89 jours. Vers l'an 1250 de notre ère, lorsque le périhélie et le solstice de décembre se confondaient, l'automne était égal à l'hiver, le printemps à l'été, et ces deux dernières saisons réunies donnaient déjà la somme de jours la plus élevée. Lorsque l'équinoxe de printemps et le périhélie se confondront, vers 6485, le printemps sera égal à l'hiver, l'été à l'automne, et ces deux dernières saisons seront les plus longues. Puis, vers le CXIX^e siècle, ce sera au tour du solstice de juin à être rejoint par le périhélie, et ainsi de suite, le mouvement de rapprochement étant de 61,9 s par an, correspondant à un cycle d'un peu moins de 21 000 ans, et l'ordre de longueur des saisons changeant à mesure. Dans l'hémisphère Nord,  en 1900, les saisons ont commencé (temps civil moyen) : le printemps, le 24 mars à 1,48 h; l'été, le 21 juin à 21, 49 h; l'automne, le 23 septembre à 0,29 heure; l'hiver, le 22 décembre à 6, 51 h. 

Le printemps - Il commence lorsque le Soleil, s'avançant vers le zénith, a atteint une hauteur méridienne moyenne; c'est-à-dire, lorsqu'il est arrivé au point de l'écliptique qui coupe l'équateur, et il finit lorsque le Soleil, continuant de s'approcher du zénith, a atteint sa plus grande hauteur méridienne, c'est-à-dire, lorsqu'il est arrivé au point de l'écliptique qui coupe le colure des solstices : ainsi pour les habitants de l'hémisphère boréal, au moins pour les habitants de la zone tempérée boréale, le printemps, qui suit l'hiver et précède l'été, commence le 20 ou 21 mars; et il finit le 21 ou 22 juin. Mais pour les habitants de la zone tempérée australe; le printemps commence le 22 ou 23 septembre; et il finit  le 21 ou 22 décembre. Au printemps dans un hémisphère correspond l'automne dans l'hémisphère opposé.

L'été- Il commence lorsque le Soleil, s'approchant de plus en plus du zénith, a atteint sa plus grande hauteur méridienne; c'est-à-dire, lorsqu'il est arrivé au point de l'écliptique, qui coupe le colure des solstices; et il finit, lorsque le Soleil, s'éloignant ensuite de plus en plus du zénith, est parvenu à une hauteur méridienne moyenne entre sa plus grande et sa plus petite; c'est-à-dire, lorsqu'il est arrivé au point de l' écliptique qui coupe l'équateur. Ainsi pour ceux qui habitent l'hémisphère septentrional, au moins pour les habitants de la zone tempérée et de la zone glaciale septentrionales, l'été commence le 21 ou 22 juin; et il finit  le 22 ou 23 septembre. Mais, pour les habitants de la zone tempérée et de la zone glaciale méridionales, l'été commence le 21 ou 22 décembre; et il finit le 20 ou le 21 mars. 

Le jour le plus long. - Le jour où l'été commence, correspond au jour naturel le plus long de l'année, et à la nuit la plus courte; c'est-à-dire, que le Soleil demeure au-dessus de l'horizon le plus longtemps et au-dessous le moins de temps qu'il est possible pour chaque lieu : et la différence de la longueur du jour à celle de la nuit est d'autant plus grande, que le lieu dont il s'agit, a une plus grande latitude.

L'automne - Dans l'hémisphère Nord, il commence au moment de l'équinoxe d'automne, qui termine l'été (le 22 ou 23 septembre), et s'achève au moment du solstice d'hiver, qui marque le début de l'hiver (le 21 ou 22 décembre). Les jours naturels sont égaux aux nuits, à l'équinoxe. Ils diminuent tout au long de l'automne, pour atteindre leur durée minimale au moment du solstice (Les Jours et les Nuits). Comme les saisons sont inversées dans l'hémisphère Sud, la saison correspondante est le printemps.

L'hiver - Il commence lorsque le Soleil, s'éloignant de plus en plus du zénith, est parvenu à sa plus petite hauteur méridienne, c'est-à-dire lorsqu'il est arrivé au point de l'écliptique qui coupe le colure des solstices; et il finit lorsque le Soleil, se rapprochant ensuite de plus en plus du zénith, a atteint une hauteur, méridienne moyenne entre sa plus grande et plus petite; c'est-à-dire, lorsque qu'il est arrivé au point de l'écliptique qui coupe l'équateur. Ainsi, pour ceux qui habitent l'hémisphère septentrional, l'hiver commence le 21 ou 22 Décembre; et il finit  le 20 ou 21 Mars. Mais pour les habitants de l'hémisphère méridional, l'hiver commence le 21 ou 22 Juin, et il finit  le 22 ou 23 septembre.

La nuit la plus longue. - Le jour où l'hiver commence, est celui qui est le plus court de l'année, et la nuit, plus longue, c'est-à-dire, que le Soleil demeure au-dessus de l'horizon le moins de temps, et au-dessous le plus longtemps qu'il est possible pour chaque lieu; et la différence de la longueur du jour à celle de la nuit est d'autant plus grande, que le lieu dont il s'agit a une plus grande latitude.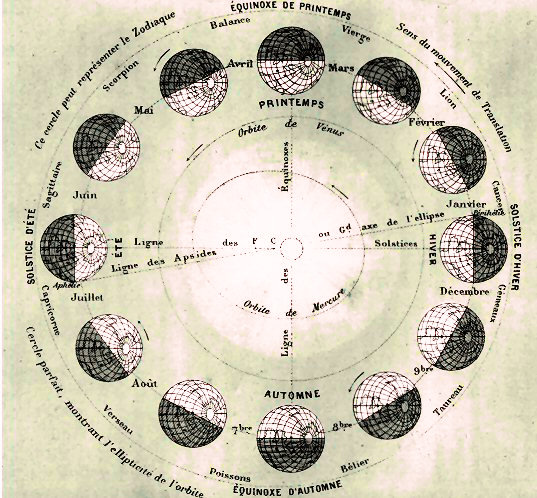

Les saisons météorologiques.
Le Soleil étant notre source de chaleur, il semblerait que la température dût être le plus élevée lorsqu'il est le plus près de la Terre, c.-à-d. lorsque celle-ci passe au périhélie, le 2 janvier. Or, dans  les régions septentrionales de latitudes moyennes et élevées, c'est justement l'époque de l'année la plus froide et pourtant la distance entre l'astre et sa planète n'est alors que de 145, 7 millions alors qu'au début juillet, au passage à l'aphélie, elle est de 154, 800 km, soit  environ 6 millions de kilomètres de plus. 

La cause déterminante des saisons météorologiques réside ailleurs. C'est l'inclinaison de l'axe de la Terre sur son orbite qui, en faisant varier, chaque jour, la hauteur méridienne du Soleil et l'intervalle de son lever à son coucher (jour naturel), produit, entre l'été et l'hiver, les différences observées. Dans l'hémisphère boréal, par exemple, la hauteur méridienne du Soleil va sans cesse en augmentant du solstice de décembre au solstice de juin, en même temps que la durée du jour surpasse de plus en plus la durée de la nuit. Les rayons solaires arrivent ainsi de plus en plus verticalement et pendant un temps de plus en plus long. Du solstice de juin au solstice d'été, l'inclinaison des rayons et le temps durant lequel ils frappent la terre vont au contraire sans cesse en diminuant et repassent, dans l'ordre inverse, par les mêmes valeurs. Il en résulte que notre hémisphère reçoit, de l'équinoxe de mars à l'équinoxe de septembre, une quantité de chaleur bien plus considérable que de l'équinoxe de septembre à l'équinoxe de mars : c'est l'été, ou saison chaude, et réciproquement, dans l'autre hémisphère, dans l'hémisphère austral, où les phénomènes sont d'ordre diamétralement opposé, l'hiver, ou saison froide. 
-

 

La canicule* Dans l'Antiquité, c'était le moment de l'année correspondant à la période du lever héliaque de la constellation soit du Petit Chien (Canicula), soit plus certainement du Grand Chien, marqué par l'apparition de l'étoile que les Grecs appelaient Sirius et les Égyptiens Sothis.  Cette étoile jouait un grand rôle dans l'astronomie égyptienne des temps reculés : son lever héliaque qui avait lieu vers le solstice d'été un peu avant les inondations du Nil, en était regardé comme le précurseur. L'annonce de cette heureuse invasion des eaux avait fait mettre Sothis au rang des divinités bienfaisantes de l'Égypte. Mais, comme le lever héliaque de Sirius était l'avant-coureur des grandes chaleurs et des maladies pernicieuses, pour les autres peuples, la canicule était regardée comme une divinité malfaisante. Suivant Hippocrate et Pline, « Le jour où la canicule se lève, la mer bouillonne, le vin tourne, les chiens deviennent enragés, la bile augmente et s'irrite, tous les animaux tombent en langueur et dans l'abattement; les maladies qu'elle cause le plus souvent sont les fièvres ardentes et continues, la dysenterie et les frénésies. »  Pour conjurer les influences malignes de la canicule, les Romains lui sacrifiaient tous les ans un chien roux. Suivant les anciens auteurs, la canicule passait pour la chienne d'Erigone, ou pour le chien donné par Zeus à Minos, qui en fit cadeau à Procris et ce dernier le transmit à Céphale. Les jours caniculaires sont ceux qui précèdent ou suivent le lever héliaque de la canicule : ce sont les plus chauds de l'année. On les comptait habituellement du 22 juillet au 23 août, pendant que le Soleil était dans le signe du Lion (Zodiaque). Ils indiquaient le commencement de l'année pour les Égyptiens et les Éthiopiens. (L. Barré).

Enfin, et à situation analogue, la température moyenne est plus élevée dans l'hémisphère boréal que dans l'hémisphère austral. Cela tient partie à ce que la surface baignée par les mers est moins grande dans le premier que dans le second, partie à ce que le temps durant lequel le soleil reste dans le premier est plus long de huit jours, chaque année, que celui durant lequel il reste dans le second. On a vu, en effet, plus haut que de l'équinoxe de mars à l'équinoxe de septembre (printemps et été de notre hémisphère), il y a eu tout 186 jours 11 heures et de l'équinoxe de septembre à celui de mars,178 jours 19 heures seulement. On a vu aussi que le rapport se trouvera, un jour, renversé. 

D'autres critères que la température peuvent également être pris en compte. Dans les régions tropicales, il est ainsi souvent plus pertinent de considérer les conditions pluviométriques et de parler de la saison des pluies et de la saison sèche, par exemple. On ne s'étonnera donc pas que selon les lieux et les époques les saisons aient des définitions différentes. Et cela sans rien dire de ce que les poètes peuvent aussi avoir dire des saisons à l'occasion...

Les anciens divisaient déjà l'année en saisons, d'après les variations de la température. Dans l'Inde, où cet usage semble avoir pris naissance, on n'en comptait que trois : le printemps, l'été, l'hiver. Les Grecs firent d'abord de même; puis ils ajoutèrent une quatrième saison, l'automne, et les Romains adoptèrent leur division. Dans le Nord de l'Europe, et sauf peut être chez les Germains, qui admettaient un printemps, ou ne connaissait que l'été et l'hiver. Chez les Arabes, on suivait la division tripartite des Indiens.

En librairie - Pierre Causevet et Liliane Sarazin, Les saisons et les mouvement de la Terre, Pour la Science, 2001; Jean-Paul Parisot, Françoise Suagher, Calendriers et Chronologie, Masson, 1996  (Une bonne introduction aux calendriers et au manières dont les astronomes définissent leurs différentes mesures du temps). - Marié-Davy, Les climats français au XIXe siècle.