On considérait généralement au XIX^e siècle comme démontré expérimentalement que la forme de la Terre est un ellipsoïde de révolution autour de l'axe des pôles; les éléments qui semblaient le mieux satisfaire aux diverses mesures géodésiques sont, d'après Bessel (1841) : 6 356 080 mètres, pour le petit rayon (demi-axe des pôles); 6 377 898 mètres pour le demi-diamètre de l'équateur; et donc, pour l'aplatissement, ou la différence des deux axes divisée par l'axe le plus grand : 1/299. Airy en 1848, trouve à peu près les mêmes nombres. De son côté James Clarke donnera en 1858 un rayon équatorial  de 6 378 249,2 m, un  rayon polaire de 6 356 515,0 m, soit une aplatissement de 1/293,46. Des chiffres désormais  proches de ceux qui sont adoptés aujourd'hui. Tout n'était pas réglé pour autant. 

Par exemple, Puissant, dans un mémoire lu à l'Académie des Sciences, avait déclaré en 1836 que Delambre et Méchain avaient commis une erreur dans la mesure de la méridienne de France; c'est pourquoi l'Observatoire de Paris fut conduit à déléguer Villarceau, de 1861 à 1866, pour vérifier les opérations géodésiques en huit points de la méridienne de France, au moyen de déterminations astronomiques de longitudes, de latitudes et d'azimuts. Quelques-unes des erreurs dont étaient entachées les opérations de Delambre et Méchain furent alors corrigées; en 1870, Perrier fut chargé de reprendre la triangulation entre Dunkerque et Barcelone. Il employa pour mesurer les angles des instruments plus parfaits, construits par E. Brunner, avec des microscopes au lieu de verniers; il remplaça la méthode de répétition par celle de réitération; il détermina les différences de longitudes au moyen de l'électricité; il supprima les sources d'erreurs sur la mesure des angles en se servant de signaux qu'il faisait construire, au lieu d'employer des signaux naturels, en modifiant d'une manière heureuse l'héliotrope de Gauss, en faisant de nombreuses vérifications. De 1870 jusqu'à sa mort, il dirigea les opérations. En 1879, celles-ci étaient terminées entre Perpignan et Melun.

Ces corrections et ses affinement ne constituent cependant pas l'essentiel des soucis de l'époque. T.-F. de Schubert émit l'idée que la Terre avait la forme d'un ellipsoïde à trois axes inégaux. Mais on comprit vite que les données disponibles étaient  insuffisantes pour résoudre définitivement le problème. II était nécessaire d'étendre le réseau des triangulations à la Terre entière, alors que jusque là, la plupart des mesures avaient concerné l'Europe. L'effort international nécessaire fut coordonné par le biais de l'Association géodésique internationale, fondée à Berlin en 1864 / 67, et au sein de laquelle se dérouleront ensuite tout les grands débats géodésiques. Il fallait aussi mesurer non seulement la longueur des arcs méridiens aux différentes latitudes, mais aussi mesurer les arcs de parallèles. Tâche, devenue théoriquement possible grâce, notamment aux progrès de l'horlogerie, qui permettaient désormais une bien meilleure connaissance des longitudes, mais que la géographie même de notre globe rendait en pratique bien difficile. 

Enfin, pour des raisons qui intéressaient aussi les militaires, désireux de posséder des cartes précises, il devenait opportun de déterminer les différentes irrégularités à la surface de la Terre (les variations d'altitude par rapport à l'ellipsoïde de référence, ou plutôt au géoïde, qui définit la forme moyenne de notre planète) à partir de mesures appelées des nivellements. Un programme d'autant plus compliqué, on avait remarqué qu'en certains endroits le fil à plomb était dévié de la position qu'il devrait occuper si la Terre avait été un corps homogène, et que cette déviation n'était pas toujours l'effet des masses montagneuses. Ce constat a conduit à l'idée de rechercher si les anomalies constatées n'étaient pas dues à des dépôts en ces endroits de métaux plus denses que la Terre ou à l'absence de matières dans de grandes cavités. Les préoccupations de la géodésie rejoignaient celles de la géologie. C'est ainsi d'ailleurs qu'en 1862, H. Faye signala au Bureau des Longitudes l'importance des travaux géodésiques anglais et russes dans ces domaines, et lui a proposé des conclusions tendant surtout à réunir les nivellements et les reconnaissances géologiques, afin de calculer les déviations produites par les attractions locales dans la direction de la pesanteur.

La réalité de l'aplatissement aux pôle de notre globe, étant accéptée dès la fin du siècle précédent (La géodésie aux XVII^e et XVIII^e siècles), l'objectif de la géodésie au XIX^e siècle va consister pour une large part à déterminer les irrégularités de la surface terrestre, par rapport à une surface ellipsoïdale moyenne ou surface osculatrice. Mais, pour atteindre à ce but, les opérations géodésiques devront pouvoir embrasser des arcs situés en nombre égal dans toutes les portions du globe. Or à cette époque tous les arcs méridiens mesurés sont localisés en Europe sur un espace de 20° en longitude, compris entre l'arc anglo-franco-espagnol et l'arc russe, si l'on excepte les arcs équatoriaux de l'Inde et du Pérou et l'arc du cap de Bonne-Espérance et quelques mesures en Inde ou aux États-Unis (mesure d'un arc d'un degré et demi en Pennsylvanie par Mason et Dixon). 

Jusqu'à 1850 - La triangulation des îles Britanniques, que Roy, Mudge et Kater commencèrent en 1784, fut terminée en 1802 par la mesure d'un arc de méridien; elle s'appuie sur beaucoup d'observations astronomiques, qui lui donnent une grande valeur au point de vue de la détermination générale de la forme de la Terre. La triangulation de l'Inde anglaise fut initiée par Kater, puis dirigée de 1802 à 1823 par Lambton et de 1823 à 1843 par G. Everest.

Au Danemark, Schumacher a donné en 1817 le programme des travaux géodésiques et Hansen a triangulé en 1821 le duché de Holstein.

La première triangulation des Pays-Bas a été faite de 1802 à 1814 par Krayenhoff, qui a publié à La Haye en 1827 un précis historique de ses opérations géodésiques.

Les triangulations ont été commencées en 1810 en  Bavière et dans le Palatinat, et en 1818 dans le reste de l'Allemagne. De 1821 à 1824, Gauss a mesuré un arc de méridien entre Göttingen et Altona et un arc de parallèle en Hanovre, en employant des méthodes originales et un instrument qu'il a inventé, l'héliotrope, pour viser les sommets éloignés des triangles.

En Russie, les travaux géodésiques ont été dirigés par W. Struve et T.-F. de Schubert respectivement à partir de 1816 et de 1820.

En Italie, une triangulation pour déterminer un arc de méridien entre Rivoli et la mer Adriatique fut commencée en 1785 par Oriani, continuée en 1803 par Puissant et achevée en 1811 par les ingénieurs-géographes français. Une autre triangulation fut faite de 1821 à 1821 pour mesurer l'arc de parallèle à 45° qui traverse la Savoie et le Piémont; mais les résultats des opérations géodésiques, qui furent difficiles dans les Alpes, a cause des neiges, ne s'accordèrent pas avec ceux des observations astronomiques faites par Carlini et Plana; et ce dernier attribue les différences à une irrégularité de densité des couches terrestres dans la chaîne des Alpes.

On voit d'après cela qu'il était encore indispensable, pour asseoir des conclusions solides, de mesurer un arc aux États-Unis aussi long que possible à l'Est des montagnes Rocheuses, un autre arc au Chili le long de la côte, un autre arc en Égypte dans la vallée du Nil, d'étendre celui du Cap et enfin de mesurer un arc en Australie et un autre en Indochine dans la vallée du Mékong. Un arc dans la vallée du Para et un autre au Brésil seraient également très bien placés estimait-on, mais l'entreprise n'est semblait plus difficile à réaliser. Quant à la triangulation de l'Afrique intérieure, elle semblait encore irréalisable avant de longues années. Les efforts effectués par la France, pour prolonger le méridien français au Sahara jusqu'à Ghardaïa, paraissaient réaliser tout ce qu'il est possible de tenter dans le Nord de l'Afrique, si ce n'était dans la vallée du Nil évidemment plus accessible. Malheureusement pour la paix européenne, les grandes puissances paraissaient avoir dans la vallée du Nil des préoccupations fort étrangères à la vérification du degré de Sennâar, et les savants plaçaient plutôt leurs espoirs dans la mesure de l'arc de méridien en Indochine.

Après 1850 - En France, pour la Carte de l'État-Major, initiée en 1818, la mesure de triangles de premier et de second ordre fut achevée en 1854, et celle des triangles de troisième ordre en 1863.

Dans les Îles Britanniques, les principaux travaux géodésique ont été faits par l'Ordnance Survey Office, qui date de 1791. La triangulation de l'Inde anglaise a été dirigée de 1843 à 1861 par A. Waugh, et de 1861 à 1878 par J.-T. Walker; elle comprend la mesure d'un arc de méridien de 21°.

En Belgique, les triangulations ont été faites de 1853 à 1873.

Au  Danemark, les triangulations ont été terminées en 1870. Andrae a fait achever en 1867 la mesure d'un arc de méridien et d'un arc de parallèle se rattachant à ceux que Gauss avait mesurés. II en a publié les résultats de 1867 à 1885 dans son ouvrage intitulé Den danske Gradmaaling (1867-1885), dont une partie rédigée en français a pour titre Problèmes de haute Géodésie (1881).

Aux Pays-Bas, les travaux ont été repris en 1861.

En Bavière et le Palatinat, les opérations géodésiques ont été achevées en 1854. Dans le reste de l'Allemagne, elles ont été continuées en 1847 par Baeyer. Elles embrassent la mesure, terminée en 1877, de l'arc du parallèle à 52° compris entre les frontières belge et russe.

En Autriche et en Hongrie, l'Institut militaire géographique de Vienne a fait mesurer, de 1862 à 1890, des chaînes de triangles dans la direction de trois parallèles et de six méridiens.

En Russie, W. Struve et T.-F. de Schubert terminèrent leurs travaux géodésiques respectivement en 1855 et en 1862.

Les triangulations de premier ordre dans les diverses parties de l'Italie furent faites surtout de 1836 à 1863; les autres travaux se sont continués depuis cette époque.

Les grandes triangulations de l'Espagne, commencées en 1859 à Madrid par une Commission militaire, avec des instruments précis, ont été terminées en 1877 à Ares par l'institut géographique, sous la direction d'Ibañez.

En 1895, Defforges a présidé, sur la demande du gouvernement de la Roumanie, à la mesure des trois bases fondamentales de la Carte militaire de cette contrée. Ensuite, sur la demande du gouvernement de la Porte, la France l'a envoyé en mission officielle pour organiser le service de la Carte militaire de l'Empire ottoman). En février 1897, la base centrale était mesurée, les coordonnées de départ déterminées astronomiquement et les triangulations commencées. Les opérations, interrompues par la guerre turco-grecque, se continueront ensuite.

Jusqu'en 1862, on avait mesuré dans l'Europe deux grands arcs de méridiens : l'arc hispano-franco-anglais de 22° 40', s' étendant de Formentera, dans les îles Baléares, à Saxavord, dans les îles Shetland, et l'arc russo-scandinave de 25°20', compris entre Hammerfest, sur les bords de la mer Glaciale, et Ismaïl, sur les bords du Danube; trois petits arcs de méridiens en Hanovre, en Danemark et dans la Prusse orientale; deux arcs de parallèles, l'arc franco-sarde-autrichien de Marennes à Orsova et l'arc franco-bavarois-autrichien de Brest à Vienne. En Russie, les observations furent faites par la méthode de W. Struve.

Le Bureau hydrographique des États-Unis a terminé en 1878, entre les États du Maine et de Géorgie, une triangulation ayant 18° de longitude et 12° de latitude.

De 1837 à 1849, Antoine d'Abbadie a fait des levés en Abyssinie par les méthodes de la Géodésie expéditive; il expose ces méthodes et donne les résultats de ses observations dans sa Géodésie d'une partie de la Haute-Éthiopie (1860-1874), publiée avec la collaboration de R. Radau pour les calculs et la construction des cartes.

Les Cartes marines étaient, jusque vers 1845, établies par des levés sous voiles, qui ne donnaient que des croquis, ou par des procédés géodésiques souvent impraticables dons les pays sauvages. Mouchez les établit par une méthode mixte consistant à employer des points fixes déterminés par des observations astronomiques faites à terre; et pour cela il avait fait modifier par J. Brunner, en 1849 et en 1856, la lunette méridienne pour la rendre portative. Il levait rapidement et avec assez d'exactitude les contours d'une côte ou d'une baie, en faisant avec le théodolite un petit nombre de stations sur des points culminants. Vers 1850, il introduisit dans la manière de faire le point une modification qui fut ensuite pratiquée sous le nom de méthode américaine. Il établit de 1867 à 1873, sur une étendue de 800 km, la Carte des côtes de l'Algérie, qui n'étaient connues que par le levé sous voiles fait de 1831 à 1835 par Bérard et de Tessan. Il est bon de remarquer que, dans les levés de reconnaissance des côtes, on commence à obtenir à cette époque les angles avec rapidité et une précision suffisante en employant la chambre claire de Wollaston modifiée par A. Laussedat en 1854.

La mesure d'un arc de parallèle en Algérie

Les mesures d'arcs de méridien ne sont pas les seules opérations que l'on puisse entreprendre pour déterminer les dimensions de l'ellipsoïde terrestre. Les arcs de parallèle pourraient être d'un grand secours, s'il était possible d'en déterminer l'amplitude avec sûreté.  Ainsi, alors que pour l'étude de la forme de la Terre, on n'avait employé jusqu'en 1864 que des arcs de méridiens, parce qu'on n'avait ni méthode, ni instruments permettant d'obtenir avec une précision suffisante les amplitudes célestes des arcs de parallèle, l'État-Major français chargea Perrier de diriger en Algérie les opérations de mesure d'un arc de parallèle terrestre; c'est dans ce pays qu'à partir de 1867, Perrier se servit, pour remplacer le cercle répétiteur, d'un cercle réitérateur qu'il avait fait construire par E. Brunner. Il fit mesurer deux bases ayant une longueur d'environ 10 km, l'une à Oran, l'autre à Bône, En 1869, la triangulation de l'Algérie était terminée dans la région du Tell et il ne restait plus, pour fixer la place de cette région sur le sphéroïde terrestre, qu'à mesurer la longitude, la latitude et un azimut en une station centrale, qui fut la ville d'Alger. La mesure de la différence de longitude entre Paris et Alger fut faite en 1874 par Perrier, qui resta dans la première ville, et par Loewy, qui se rendit dans la seconde. Pour cette mesure, sur la proposition de Le Verrier, l'enregistrement électrique fut appliqué à l'observation des passages et à l'échange des signaux. Le nombre ainsi trouvé concordait avec celui que Loewy et Stéphan avaient obtenu à la même époque au moyen de deux opérations, l'une entre Paris et Marseille, l'autre entre Marseille et Alger. Ensuite, Perrier, installé dans un Observatoire qu'il avait établi sur le plateau de Voirol, dominant les collines de Mustapha, trouva le latitude d'Alger par l'observation des distances zénithales méridiennes de 46 étoiles voisines du zénith. II détermina, en 1874 et en 1878, l'azimut d'un point de repère situé sur un mamelon élevé de l'Atlas et très voisin du méridien d'Alger, Ia latitude et l'azimut de Bône et de Nemours, villes voisines des extrémités de l'arc de parallèle mesuré, et les différences de longitude entre ces trois villes; il a apporté un soin tout particulier au calcul des positions géographiques, en faisant, pour obtenir la concordance des bases, des corrections sur les angles d'après une méthode que Laplace donne dans sa Théorie analytique des probabilités (1812). Des résultats que Perrier trouva en mesurant un arc de parallèle algérien de 9°36', il résultait que la courbure de la Terre devait être irrégulière dans la région où se trouve cet arc.

Malheureusement, il n'est pas encore envisageable, au XIX^e siècle, de répondre d'une différence de longitude à moins de 1"5, erreur double de celle que l'on peut craindre sur l'amplitude d'un arc de méridien. D'ailleurs, l'inégale distribution des terres dans les deux hémisphères ne permet pas, à de très rares exceptions, de mesurer des arcs de parallèle symétriques par rapport à l'équateur et compris entre les mêmes méridiens; une telle recherche perd le grand intérêt qu'elle présenterait en fournissant, dans le cas d'identité, la preuve expérimentale de la similitude des deux hémisphères. On cite quand même, comme pouvant servir à cette démonstration, des arcs de 50° N. et S. de latitude compris entre les méridiens de 70° et 80°, c.-à-d. à la hauteur de l'embouchure du Saint-Laurent dans l'Amérique du Nord et vers la pointe de l'Amérique du Sud, puis les arcs de 30° en Afrique s'étendant, d'une part, d'Alexandrie aux confins occidentaux de la Tripolitaine, le long de la Méditerranée et, de l'autre, des rivages de l'océan Indien à ceux de l'Atlantique à quelques centaines de kilomètres au Nord de ce qui est alors colonie du Cap (L'Afrique australe). Enfin, à la même distance de l'équateur, un petit arc de parallèle en Australie et un autre en Chine. mais dans ce dernier cas, les savants de l'époque se demandent  s'il leur sera jamais possible de pénétrer à l'intérieur de l'Empire Céleste, à quelque profondeur dans les terres...
-
Les jonctions géodésiques

La jonction géodésique de la France avec l'Angleterre.
Avant 1861, le travail de jonction des triangulations de la France avec l'Angleterre, par-dessus le détroit du Pas-de-Calais, avait été plusieurs fois entrepris par des géodésiens de ces deux pays, mais sans succès, parce que les signaux ordinaires ne pouvaient être nettement aperçus d'une rive du détroit à l'autre rive. Dans les années 1861 et 1862, cette jonction  fut opérée séparément et simultanément, en se servant de l'héliotrope de Gauss, par deux Commissions composées, l'une d'ingénieurs anglais, notamment H. James et M. Clarke, l'autre d'officiers français, dont le chef, Levret, eut Perrier pour collaborateur le plus actif. Des travaux de ces deux Commissions, il est résulté la mesure d'un nouvel arc de la méridienne de France, ayant 13° et s'étendant de Dunkerque aux îles Shetland.

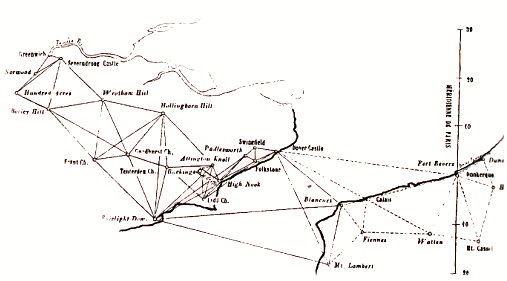
Carte de la la jonction des côtes françaises et anglaises,
publiée par Arago dans son Astronomie populaire (1859).

La jonction géodésique de l'Algérie avec l'Espagne. 
Levret avait prouvé en 1863 que la jonction géodésique de l'Algérie avec l'Espagne, par-dessus la Méditerranée, était théoriquement possible, parce que la courbure de la Terre n'intercepte pas la trajectoire des rayons visuels allant de l'Atlas aux sierras de Grenade et de Murcie. Perrier reconnut en 1868 sur le terrain même que cette jonction était matériellement possible. En 1873, Ibañez et Perrier, qui dirigèrent les opérations de cette jonction, choisirent les stations très élevées de Mulhacen et Tetica en Espagne, de Filhaoussen et M'Sabiha en Algérie, formant un quadrilatère dont chaque sommet est visible de chacun des trois autres. Comme les signaux devaient être perceptibles à des distances d'environ 300 km, ils durent avoir recours à la lumière solaire pendant le jour et à la lumière électrique pendant la nuit. Pour les signaux de nuit, ils se servirent d'appareils que venait d'imaginer A. Laussedat. Ce fut un travail très difficile que de faire transporter à de si grandes hauteurs une machine magnéto-électrique de Gramme, une machine à vapeur pour l'actionner et les instruments géodésiques. Malgré ces difficultés, malgré les attaques des tribus hostiles à la présence française, malgré la gêne apportée par le ciel brûlant de l'Algérie et par les neiges couvrant à la fin de l'été la montagne de Mulhacen, les observateurs réussirent pleinement à opérer la jonction projetée, grâce aux signaux électriques de nuit qui seuls furent aperçus. Les observations, commencées le 9 septembre, se terminèrent le 1^er octobre. L'opération géodésique fut complétée du 5 octobre au 16 novembre, par le rattachement des réseaux astronomiques de l'Espagne et de l'Algérie. Ainsi se trouvait réalisé, au moyen des plus grands triangles qui aient été mesurés, un voeu émis par Biot et Arago à leur retour d'Espagne.

L'Association géodésique internationale

Tous ces desiderata supposaient des actions concourantes bien diverses. Dans ce but, les géodésiens ont fondé l'Association géodésique internationale, dont la tâche était d'examiner en commun les moyens les plus propres à faire progresser la science géodésique, en assurant une direction aux travaux entrepris par chaque nation. 
Fondée à Berlin en 1864 sous l'initiative du général Baeyer, l'Association pour la mesure du degré dans l'Europe centrale prit en 1867 le titre d'Association géodésique internationale, après l'adhésion de la Russie et de l'Espagne. Pour comprendre dans son domaine toutes les mesures effectuées hors de l'Europe, l'Association géodésique internationale fut réorganisée; après la mort de son fondateur Baeyer : le Gouvernement prussien prit l'initiative de la réforme. Dans une Conférence tenue à Berlin en octobre 1886, les délégués des principales contrées de l'Europe, la Turquie et l'Angleterre exceptées, et de quelques contrées des autres parties du Monde, décidèrent que l'Association géodésique internationale avait pour but la mesure des degrés de toute la Terre; qu'elle aurait à Berlin un Bureau central de calculs; qu'une Commission permanente, composée de 11 membres, se réunirait tous les ans, dans une ville des États associés; que l'Association aurait tous les trois ans une réunion plénière où la Commission permanente serait renouvelée par moitié. Ibañez fut alors nommé président de cette Commission et R. Helmert directeur du Bureau central des calculs.

La conférence générale se réunira désormais dans l'une des capitales des États associés; une commission permanente composée de membres choisis parmi les délégués se réunit chaque année dans une ville différente; les délégués qui n'en font pas partie sont invités à assister aux séances, mais sans droit de vote. La commission permanente s'occupe de la publication des rapports communiqués par les délégués sur les travaux géodésiques exécutés dans leurs pays et sur leurs propres recherches. Un organe spécial de l'Association, appelé bureau central, classe et conserve les archives; il rédige en outre un rapport général et s'occupe des questions relatives à l'uniformité des mesures géodésiques et, astronomiques. L'Association possède un budget alimenté au moyen de cotisations annuelles versées par les États adhérents.

Les premières réunions - La Commission permanente, par les réunions annuelles et par les Congrès de Berlin en 1864 et en 1867, de Vienne en 1871, de Dresde en 1874, est arrivée à résoudre d'une manière jugée alors satisfaisante les questions que posaient la géodésie à cette époque. La France, qui avait été l'initiatrice des travaux de mesure de la Terre, étaient restée à peu près stationnaire, pendant que les autres pays couvraient leur sol de triangulations en employant de meilleurs instruments et procédés d'observation et de calcul. Elle hésita même longtemps avant de céder aux instances de l'Association qui lui demandait de prendre part à ses travaux. Ce fut seulement en 1871 qu'elle commença à en faire partie et désigna Delaunay pour la représenter au Congrès de Vienne. En 1874, H. Faye fut nommé membre de la Commission permanente. L'Association vint tenir à Paris, en 1875, sous la présidence d'Ibañez, un congrès, où fut décidée la construction d'une règle géodésique internationale pour la mesure des bases et où Perrier déclara que les observations de nuit sur les repères d'une triangulation "donnent une précision au moins égale, sinon supérieure aux observations de jour ".

A la réunion de la Commission permanente à Nice en 1887, l'empereur du Brésil Dom Pedro d'Alcantara déclara que le Brésil ferait partie de l'Association; cette accession présentait un grand intérêt, parce que l'on n'avait presque pas encore de mesures dans l'Amérique du Sud. Ch. Lallemand a démontré la nécessité d'apporter aux résultats des nivellements de précision une correction due aux variations de la pesanteur.

A la Conférence générale de Paris en 1889, G. Davidson a annoncé l'accession des États-Unis à l'Association géodésique et a demandé une nouvelle mesure de l'arc du Pérou avec toutes les ressources de la science moderne.

Plusieurs questions ont été discutées dans la réunion de la Commission permanente à Fribourg en 1890. Bouquet de la Grye et Ch. Lallemand ont lu chacun un mémoire sur le choix d'un zéro unique pour les nivellements. Comme les recherches de la géodésie exigent que les points soient rapportés à une même surface, l'Association s'était déjà occupée de la question difficile du zéro unique; elle avait d'abord conseillé d'installer dans les ports des instruments, appelés marégraphes, pour enregistrer les variations du niveau des mers, ce qui fut fait dans plusieurs ports; elle avait demandé que les nivellements fussent faits deux fois et en sens inverses pour s'assurer de leur degré d'exactitude. Dans son mémoire, Bouquet de la Grye, se basant sur ses nombreuses observations à Brest, est favorable au projet de prendre pour surface fondamentale le niveau moyen de l'Océan; il montre que l'on peut obtenir rapidement le niveau moyen de la mer et faire facilement les corrections dues aux marées et aux vents, en appliquant les formules qu'il donne. 

Ch. Lallemand a été porté par ses recherches à penser que toutes les mers ont le même niveau moyen : il en résulterait, précise-t-il, que la question du zéro unique perd de son importance. Defforges a parlé de ses recherches sur la loi de décroissance des amplitudes du pendule. Les membres ont discuté la question de la variation des latitudes. La détermination exacte des latitudes terrestres est importante en astronomie, parce que les latitudes servent à trouver les déclinaisons des étoiles, et en géodésie, parce que, pour calculer la forme de la Terre et obtenir les amplitudes des arcs de méridien mesurés, on détermine les différences des latitudes. En comparant les latitudes mesurées avec soin en 1889 et en 1890, à Berlin, à Potsdam et à Prague, le Bureau central il conclu que la latitude a une variation périodique d'environ une demi-seconde. Villarceau, de 1856 à 1861, avait aussi trouvé à Paris des variations annuelles de la latitude. Il paraissait dès lors probable qu'il s'agissait d'un phénomène général. La question de la variation des latitudes, qui préoccupait les astronomes, a été examinée avec soin en 1891 par R. Radau dans un des chapitres du Traité  de Mécanique céleste de Tisserand.

Dans la réunion de la Commission permanente à Florence en 1891, Hervé Faye a été nommé président de cette Commission en remplacement d'Ibañez. Les premiers résultats obtenus parla mission d'Honolulu relativement à la variation des latitudes ont été communiqués.  Ch. Lallemand annonça que les travaux de nivellement du réseau de premier ordre étaient presque terminés en France; R. Helmert lut un long Rapport sur la question générale des nivellements et conclut qu'il était actuellement impossible de transporter un zéro fondamental par un nivellement géométrique étendu.

Robert Helmert a déclaré dans la Conférence générale de Bruxelles, en 1892, que Chandler a pu démontrer la variation périodique des latitudes pour une longue série d'années, par la discussion de matériaux tirés des données de nombreux Observatoires. Il en résultait, ajoutait-il, que le déplacement de l'axe de la Terre dans celle-ci est la cause de cette variation, qui a une période annuelle en même temps qu'une période d'environ 14 mois  (Le Mouvement des pôles). Cette question a encore été agitée aux réunions de Genève en 1893, d'Innsbrück en 1894 et de Lausanne en 1896; H.-G. Van de Sande Bakhuyzen a présenté à Lausanne des considérations utiles sur le mode d'étude des variations périodiques de la latitude. R. Helmert a lu à Bruxelles la suite de son mémoire de Nice sur les déviations de la verticale. Ayant rapporté à l'ellipsoïde de Bessel et à celui de Clarke un grand nombre d'observations, il a reconnu que le premier s'adapte mieux aux résultats que le second et que les masses continentales exercent une attraction sur le fil à plomb.

A la Conférence générale de Berlin en 1895, Ch. Lallemand a lu, sur le rôle des erreurs systématiques dans les nivellements de précision, une note où il rappelle qu'il a indiqué en 1889, dans son ouvrage Nivellement de haute précision, une méthode graphique simple pour mettre en évidence ces erreurs et en mesurer la grandeur; il a trouvé qu'elles varient de 0,05 mm à 0,30 mm par kilomètre, dans les principaux réseaux des nivellements européens.

La Russie a apporté à l'Association la mesure, terminée en 1894, de la partie de l'arc du parallèle à 52° comprise entre Varsovie et Orsk, dans l'Oural. Cet arc de parallèle, prolongé jusqu'à l'île Valentia en Irlande, par des savants prussiens, belges et anglais, a une amplitude de 60°.

A la réunion de la Commission permanente à Stuttgart en 1898, Bakhuyzen a dit que les études de son frère et de lui-même ont confirmé l'existence d'une variation de la latitude soumise à deux périodes, l'une de 431 jours et l'autre de 365. Après une longue discussion sur la question des latitudes, les membres de la réunion ont décidé d'organiser, aux frais de l'Association géodésique, un service international de latitude avec six stations sur le parallèle à 39° 8', et ils ont proposé d'adopter la méthode de Horrebow. Notons que Moritz Loewy a proposé en 1885, pour déterminer la latitude, une méthode qui est fondée sur un autre principe que la précédente, et que l'on emploiera à l'Observatoire de Paris. Ensuite, on a examiné les Rapports des délégués de 14 Gouvernements sur l'état de la géodésie dans chaque pays. Le premier rang est occupé par l'Allemagne, où les officiers de la Landesaufnahme ont mesuré avec soin un vaste réseau de triangles. En Algérie et en Tunisie, les officiers que dirigeait Bassot ont mesuré, huit grandes bases et assurent qu'ils auront achevé dans les premières années du XXe siècle la triangulation de deux longues chaînes reliées par quatre lignes méridiennes. Enfin Bouquet de la Grye a lu son Rapport sur plus de 70 marégraphes qui fonctionnent en Europe; il a trouvé que la France emploie le type le plus simple de ces instruments, et que le niveau moyen de la mer, et par suite du sol, reste à peu près stationnaire aussi bien à Brest qu'au Havre.

Les nivellements

On appelle nivellement la suite d'opérations servant à déterminer le relief du sol relativement à la surface moyenne de la Terre. En d'autres termes, le but visé est d'obtenir les hauteurs respectives, ou altitudes, des divers points par rapport à l'ellipsoïde de révolution qui est le prolongement au-dessous des continents de la surface des mers. Les altitudes peuvent être fournies grosso modo par le baromètre. L'intervention de deux observateurs est nécessaire, l'un se tient dans une localité dont l'altitude est supposée connue et note à intervalles équidistants pression et température; l'autre se déplace et relève les mêmes données dans les endroits qu'il traverse. Les baromètres altimétriques, encore plus imparfaits, donnent l'altitude par une simple lecture; l'hypsomètre sert au même usage. Ces procédés, employés depuis le XVII^e siècle, sont encore parfois utilisés au XIX^e siècle, mais seulement faute de mieux, par exemple dans les ascensions en ballon ou sur des montagnes ou dans les explorations en pays inconnus. Désormais, la détermination des altitudes absolues dans le lever de la carte d'un grand pays reposent pour l'essentiel à des méthodes plus rigoureuses et fiables, basées ici encore sur des triangulations. 

Les anciens géodésiens se préoccupaient seulement de déterminer l'altitude des sommet des grands triangles et des points les plus importants. D'ailleurs, la construction des routes n'exigeait pas une grande exactitude, et des opérations topographiques assez grossières suffisaient pour leur tracé. Les grands travaux nécessités par les chemins de fer, tunnels, percements d'isthmes (Suez, Panama), etc., créèrent des besoins nouveaux, et une véritable science vit le jour. Le mouvement s'étendit progressivement à l'Europe entière; en France, les ingénieurs des mines et des ponts furent à la tête du progrès; ailleurs, la chose fut généralement rattachée aux services géographiques; partout l'effort fut considérable et les méthodes topographiques parvinrent rapidement à un haut degré de perfection. Il est juste d'ajouter qu'à la tête d'un personnel d'élite les ingénieurs possédaient des moyens d'action infiniment plus puissants que ceux mis à la disposition des anciens géodésiens. Bourdaloue, le premier, de 1857 à 1864, entreprit un nivellement général de la France; il couvrit le pays entier d'un réseau de polygones, leur développement atteignant 3000 km pour la partie de haute précision.

En face des résultats obtenus, l'Association géodésique internationale émit le voeu, suivi d'effet, que la chose fût étendue à l'Europe entière. La Suisse avait entreprit les premières mesures de nivellement dès 1863. L'Allemagne en 1864, la Russie en 1873 et l'Italie en 1876, imitèrent la France et la Suisse. Les méthodes furent perfectionnées par des ingénieurs, tels que Durand-Claye, le colonel Goulier, Charles Lallemand, Cheysson, etc., et il fut décidé que les mesures de Bourdaloue seraient refaites sur une échelle plus étendue. Le service du nivellement général de France, dirigé par Charles Lallemand, commença le travail en 1884; la partie principale fut terminée en 1892. 

Pour cette vaste entreprise, la surface du pays a été répartie en 32 polygones d'un développement total de 12 000 km; 17 000 repères métalliques ont été placés et serviront ultérieurement à étudier les mouvements du sol. Cet ensemble forme le réseau fondamental; dans les intervalles, 16 000 km, de cheminements secondaires fixent les altitudes et enfin un réseau de troisième ordre sera mis en place un peu plus tard. Tout cela n'est donc encore qu'un travail préliminaire; suivant l'expression de Cheysson, l'on n'a encore constitué à la fin du siècle que les grandes mailles du réseau, il reste à remplir le quadrillage, ce qui portera au cours des décennies suivantes le développement total du nivellement au chiffre énorme de 800 000 km. A ce moment, l'on pourra songer à construire des cartes d'ensemble à grande échelle, portant des courbes de niveau exactes; inutile, soulignait-on, de faire ressortir l'importance de la chose pour toutes les constructions de canaux, dérivations de rivières, etc.

Attractions locales
Les déterminations de l'intensité de la pesanteur aux différents points de la Terre étaient entrées dans le domaine de la géodésie seulement quelques années plus tôt. L'Ordnance Survey Office, dirigé par H. James, de 1854 à 1874, a déterminé les attractions locales dues au relief du sol autour des stations, pour corriger les latitudes observées. En Russie, T.-F. de Schubert proposa en 1860 de faire niveler, d'après la méthode anglaise, le terrain des stations astronomiques des principales mesures d'arcs de méridiens, non seulement en déterminant la déviation nord-sud du fil à plomb, mais aussi la déviation est-ouest. La comparaison entre les mesures astronomiques et les mesures géodésiques amena Villarceau à reconnaître que les attractions locales ont, selon une opinion qui commençait alors à se manifester, une influence sur les longitudes et les azimuts. II étudia la question d'une manière approfondie et parvint à établir en 1866 une relation qui a lieu, quelles que soient les attractions locales, entre leurs effets sur les longitudes et les azimuts. Le même Villarceau a en outre démontré en 1868 un autre théorème relatif aux attractions locales et en a tiré des conséquences qui facilitent la solution du problème de la détermination de la figure de la Terre : en 1871, il a donné une méthode de calcul pour déterminer la forme de la Terre, sans employer de nivellements proprement dits; enfin, en 1873, il compléta ses nombreuses recherches sur les attractions locales; ses travaux l'ont conduit à rejeter l'hypothèse que la Terre diffère notablement d'un ellipsoïde de révolution.

Mentionnons encore dans ce domaine les mesures de latitude et d'azimut, les déterminations télégraphiques de longitude qui sont devenus à cette même époque le complément indispensable de toute chaîne de triangles. Ajoutons encore les opérations si longues et si délicates que nécessite l'étalonnage des règles géodésiques . Signalons enfin que les divers angles qui entrent dans un réseau géodésique ne le rendent pas géométrique, ce qui revient à dire qu'un point n'occupe pas la même position, suivant qu'il est rattaché à un système de deux autres points ou à un autre, par suite des légères erreurs entachant les mesures angulaires. De là résulte la nécessité de compenser le réseau par le calcul d'un ensemble de corrections aux angles ayant pour objet d'ajuster tous les triangles, comme les pièces d'un jeu de patience. La solution du problème de la compensation dérive de l'application de la méthode des moindres carrés à la résolution des équations de condition fournies par le réseau, en nombre plus ou moins grand, suivant qu'il est plus ou moins riche, c.-à-d. que les points sont liés entre eux par un plus grand nombre de combinaisons de lignes. La compensation d'un réseau un peu compliqué comporte des calculs énormes extrêmement pénibles, malgré le secours que l'on peut tirer des toutes premières machines à calculer. Si l'on rapproche ces calculs de la masse de corrections qu'il faut faire subir aux observations de toute nature, avant d'en déduire un résultat quelconque, on voit que les travaux de cabinet poursuivis par les géodésiens sont plus longs et aussi importants que les travaux effectués sur le terrain. Une situation qui ne changera pas fondamentalement jusqu'à la seconde moitié du XX^e siècle. Elle bénéficiera alors des moyens que lui procureront d'une part les satellites, et d'autre part les ordinateurs. (Ch. de Villaedeuil / E. Lebon).