Les polynômes

Introduction

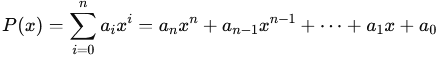 • x est l'indéterminée.

 • ai  R sont les coefficients, provenant d'un ensemble R (souvent un anneau ou un corps, comme  ou ).

 • an​ (le coefficient du terme xn) est appelé le coefficient dominant. Il influence la forme générale de la courbe représentative du polynôme.

 • n, le plus grand exposant de la variable, est un entier naturel ( n ≥0 ) appelé le degré du polynôme si an≠0.  Il détermine le comportement général du polynôme lorsque x devient très grand (positif ou négatif).

 • a0 est le terme constant , c'est-à-dire e terme sans variable, qui donne la valeur du polynôme lorsque x est égal à 0.

Exemple : Le polynôme P(x)=3x⁴ − 2x² + 5 a pour coefficients a4 = 3, a2=−2,  a0 = 5, et son degré est 4.

Égalité de polynômes.
Deux polynômes P(x) et Q(x) sont égaux si et seulement si : ils ont le même degré;  leurs coefficients correspondants sont égaux pour tous les i.

Types de polynômes.

• Polynôme constant. - Polynôme de degré 0, c'est-à-dire de la forme P(x) = a0​, où a0 ≠ 0. Exemple : P(x) = 7.

• Monôme. - Polynôme avec un seul terme non nul, de la forme P(x)=anxⁿ. Exemple : P(x) = 4x³. 

Un polynôme est donc une somme de monômes.

• Binôme : Polynôme avec exactement deux termes non nuls. Exemple : P(x) = x² − 3x.

• Trinôme. - Polynôme avec exactement trois termes non nuls. Exemple : P(x) = 2x² + 3x − 1.

• Polynôme unitaire. - Un polynôme est dit unitaire si son coefficient dominant an​ est égal à 1. Exemple : P(x) = x³ − 2x +1est un polynôme unitaire.

• Polynôme homogène. - Un polynôme est dit homogène si tous ses termes ont le même degré. Exemple : P(x, y) = x² + xy + y² (dans plusieurs variables).

• Le polynôme nul. - Le polynôme nul est le polynôme où tous les coefficients sont égaux à zéro : P(x) = 0. Le polynôme nul n'a pas de degré défini dans la plupart des conventions (parfois, on dit qu'il a un degré − ou non défini).

P(x) = 2/x + 1 (division par une variable)
Q(x) = √x - 3 (racine carrée d'une variable)
R(x) = x⁻² + 4x (exposant négatif)
S(x) = x^1/2 (exposant fractionnaire)

Un même polynôme définit une seule fonction polynomiale. L'ensemble des fonctions polynomiales est un sous-ensemble particulier de toutes les fonctions possibles. Elles ont la propriété d'être définies par une expression polynomiale. Les fonctions polynomiales sont continues et dérivables sur tout leur domaine de définition (généralement tous les nombres réels ou complexes). C'est une propriété importante qui les rend utiles dans de nombreux domaines. Les racines d'un polynôme (les valeurs de x qui annulent le polynôme) correspondent aux points où la fonction polynomiale croise l'axe des x (ses zéros).

Opérations sur les polynômes

La somme est donnée par : 

La soustraction fonctionne de la même manière, en soustrayant les coefficients :

 • Commutativité.

Addition : P(x)+Q(x) = Q(x)+P(x). 

Multiplication : P(x).Q(x) = Q(x).P(x).

• Associativité. 

Addition : (P(x) + Q(x)) + R(x) = P(x) + (Q(x) + R(x)).

Multiplication : (P(x).Q(x)).R(x) = P(x).(Q(x).R(x)).

 • Distributivité. - La multiplication est distributive par rapport à l'addition :
    P(x).(Q(x)+R(x)) = P(x).Q(x)+P(x).R(x)

sauf si les termes de plus haut degré s'annulent, auquel cas le degré diminue.

Exemple :

P(x) = 2x³+x+1, Q(x) = −2x³+5x; 
P(x) + Q(x) = (2x³−2x³)+x+5x+1 = 6x+1;
Degré : deg⁡(P(x)+Q(x)) = 1.

 P(x)=3x²+x+1, Q(x) = x⁴−2
 deg⁡(P(x)⋅Q(x)) = deg⁡(3x² + x+1) + deg⁡(x⁴−2)= 2+4 = 6

Le produit complet est : P(x).Q(x) = (3^x2+x+1)(x⁴−2). Le terme dominant est 3x⁶, confirmant que le degré est 6.

 • La division euclidienne, qui est une méthode de division de polynômes semblable à la division euclidienne d'entiers.

 • La factorisation, qui est l'écriture d'un polynôme sous forme de produit de polynômes plus simples.

Identités remarquables de base (degré 2).
Carré d'une somme : (a + b)² = a² + 2ab + b²

Exemple : (x + 3)² = x² + 2. x.3 + 3² = x² + 6x + 9

Exemple : (2y - 1)² = (2y)² - 2. 2y.1 + 1² = 4y² - 4y + 1

Exemple : x² - 16 = x² - 4² = (x + 4)(x - 4)

Exemple : (x + 2)³ = x³ + 3. x². 2 + 3. x. 2² + 2³ = x³ + 6x² + 12x + 8

Exemple : (y - 1)³ = y³ - 3.y².1 + 3. y.1² - 1³ = y³ - 3y² + 3y - 1

Exemple : x³ + 8 = x³ + 2³ = (x + 2)(x² - 2x + 4)

Exemple : 27y³ - 1 = (3y)³ - 1³ = (3y - 1)(9y² + 3y + 1)

Division euclidienne et racines

où  deg⁡(R(x)) < deg⁡(D(x)),  Q(x) et R(x) sont uniques.

Étapes de l'algorithme à la main :

Initialisation. - Écrire le dividende P(x) et le diviseur D(x).

Déterminer le premier terme du quotient : Diviser le terme dominant de P(x) par le terme dominant de D(x).

Calculer le sous-produit : Multiplier le terme obtenu par D(x) et le soustraire de P(x).

Répéter : Réitérer le processus avec le reste obtenu, jusqu'à ce que le degré du reste soit strictement inférieur à celui du diviseur.

 Résultat : Le quotient Q(x) est la somme des termes obtenus, et le dernier reste est R(x).

Esquisse de la démonstration : l'existence repose sur la construction algorithmique décrite ci-dessus. L'unicité vient du fait que si deux paires (Q1(x),R1(x)) et (Q2(x),R2(x)) satisfaisaient la relation, alors D(x).(Q1(x)−Q2(x)) = R2(x)−R1(x). Comme le degré de R2(x)−R1(x) est strictement inférieur à celui de D(x), Q1(x) = Q2(x) et R1(x) = R2(x).

Exemple.
Diviser P(x) = x³−4x²+6x−5 par D(x) = x−2.

Étapes :

1) Diviser le terme dominant de P(x) (x³) par le terme dominant de D(x) (x) :  x³/x=x².

Ajouter x² au quotient.

2) Multiplier x² par D(x) : x²⋅(x−2) = x³−2x²; soustraire de P(x) : P(x)−(x³−2x²) = −2x²+6x−5

3) Répéter avec le nouveau dividende −2x²+6x−5 : diviser −2x² par x : −2x²/x=−2x; ajouter −2x au quotient.

4) Multiplier −2x par D(x) : −2x⋅(x−2)=−2x²+4x; soustraire :−2x²+6x−5−(−2x²+4x) = 2x−5

5) Répéter pour 2x−5 : diviser 2^x par x : 2x/x=2; ajouter 2 au quotient.

 6) Multiplier 2 par D(x) : 2⋅(x−2) = 2x−4; soustraire : 2x−5−(2x−4) = −1

Résultat : Q(x) = x² − 2x + 2, R(x) = −1.

1) Écrivez les coefficients du polynôme P(x).

2) Faites une division par a en procédant comme suit :

a) Le premier coefficient est directement reporté.

b) Les coefficients suivants sont obtenus en multipliant le dernier résultat intermédiaire par a et en ajoutant le coefficient suivant.

Le dernier résultat est le reste, et les autres valeurs forment les coefficients du quotient.

Coefficients : 2, −6, 2, −4; diviseur : a=2a=2.

Étapes :

1) 2 (premier coefficient).
2) 2⋅2+(−6 )= −2.
3) −2⋅2+2 = −2.
4) −2⋅2+(−4) = −8

Racines d'un polynôme.
Définition d'une racine (ou zéro) d'un polynôme
Une racine (ou zéro) d'un polynôme P(x) est une valeur a telle que : P(a)=0. Autrement dit, substituer x par a dans P(x) donne un résultat nul.

Théorème du facteur.
Le théorème du facteur établit une relation entre les racines d'un polynôme et ses facteurs.

Si a est une racine du polynôme P(x), alors le polynôme P(x) est divisible par (x−a), c'est-à-dire : P(x) = (x−a).Q(x), où Q(x) est un autre polynôme de degré inférieur.

Exemple : Si P(x) = x³−3x²+3x−1 et P(1)=0, alors (x−1) est un facteur de P(x).

Multiplicité d'une racine.
Une racine peut apparaître plusieurs fois. La multiplicité d'une racine a est le nombre de fois où le facteur (x−a) apparaît dans la décomposition de P(x).

Si P(x) = (x−2)²(x+1) alors : 

x = 2 est une racine de multiplicité 2;

 x=−1 est une racine de multiplicité 1.

Exemples :

Si P(x)=x³−x²−2x, on peut tester x=0 : P(0)=0³−0²−2⋅0=0. Donc x=0 est une racine.

Si P(x)=x³+x2−x−1, on peut tester x=1 : P(1)=1³+1²−1−1=0. Donc x=1 est une racine. Par le théorème du facteur, (x−1) divise P(x).

Théorème fondamental de l'algèbre

n corps est dit algébriquement clos si tout polynôme non constant à coefficients dans ce corps admet au moins une racine dans ce corps. En d'autres termes, tout polynôme de degré supérieur ou égal à 1 peut être factorisé complètement en polynômes de degré 1.
Exemples :

    Le corps des nombres complexes (\mathbb{C}) est algébriquement clos, comme le stipule le théorème fondamental de l'algèbre.
    En revanche, le corps des nombres réels (\mathbb{R}) n'est pas algébriquement clos, car il existe des polynômes non constants à coefficients réels (comme (x^2 + 1)) qui n'ont pas de racines réelles.

Propriétés :

    Si un corps (K) est algébriquement clos, alors tout polynôme de degré (n) à coefficients dans (K) a exactement (n) racines (comptées avec leur multiplicité).
    Un corps algébriquement clos ne peut pas avoir d'extensions algébriques non triviales (c'est-à-dire, différentes de lui-même).

Importance :

La notion de corps algébriquement clos est fondamentale en algèbre, car elle permet de simplifier de nombreux problèmes en garantissant que tout polynôme peut être factorisé complètement.

Conséquences du théorème fondamental de l'algèbre.
Décomposition complète dans .
Tout polynôme P(x) de degré n à coefficients complexes peut être écrit comme un produit de nn facteurs linéaires (comptés avec leur multiplicité) : P(x) = an​(x−x1​)(x−x2​)...(x−xn​), où x1, x2, …, xnx sont les racines complexes de P(x) (certaines peuvent être égales si elles sont de multiplicité supérieure à 1).

Nombre de racines (multiplicité incluse).
Un polynôme de degré n a exactement n racines complexes dans , en comptant les multiplicités.

Lien avec les polynômes à coefficients réels.
Si P(x) a des coefficients réels, ses racines complexes non réelles apparaissent par paires conjugées. Ainsi : P(x)=an(x−x1)(x−x2)...(x−xn), où chaque racine xi\  implique la présence de son conjugué^​.

Applications et importance.
Résolution d'équations polynomiales.
Le théorème garantit qu'il est toujours possible de trouver une solution complexe pour tout polynôme non constant.

Étude des propriétés algébriques.
La complétude de  permet d'explorer des résultats comme la factorisation, la théorie de Galois et les systèmes dynamiques.

Lien avec la géométrie complexe.
Ce théorème montre que les racines d'un polynôme sont des points dans le plan complexe, et ces points peuvent être étudiés pour des structures géométriques ou analytiques.

Formules de Viète

Cas des polynômes de degré 2.
Un polynôme de degré 2 peut s'écrire sous la forme : P(x) = ax² + bx + c (a ≠ 0). Si x1​ et x2​ sont les racines de ce polynôme (réelles ou complexes), alors les formules de Viète sont :

Somme des racines : x1 + x2 = −b/a.

Produit des racines : x1.x2 = c/a.

Généralisation pour les polynômes de degré n.
Considérons un polynôme P(x) de degré n : P(x)=anxⁿ + an−1xⁿ⁻¹ + ... + a1x + a0 (an≠0), dont les racines sont x1, x2,…, xn​ (pas nécessairement distinctes). Les formules de Viète généralisées sont :

Somme des racines (prises avec multiplicité) : x1 + x2+...+ xn =(−an−1an)/an

Sommes des produits des racines (prises k à k) :

Produit des racines prises 1 à 1 : (an−1/an​​.
Produit des racines prises 2 à 2 : (an−2/an​​.​​.
        ...
Produit de toutes les racines : (−1)ⁿ.a0/a​​.

 • Résolution d'équations. - Les formules de Viète permettent de résoudre des équations en identifiant les coefficients et les racines.

 • Problèmes inverses. - Par exemple, déterminer un polynôme connaissant ses racines.

 • Études algébriques. - Utilisées dans les théorèmes de base de l'algèbre et la théorie de Galois.

Factorisation et relations coefficients-racines

Polynômes irréductibles.
Un polynôme est dit irréductible :

Sur  : s'il ne peut être factorisé qu'en produit de polynômes de degré 1 ou 2 à coefficients réels.

Sur  : s'il ne peut être factorisé qu'en produit de polynômes de degré 1 à coefficients complexes (grâce au théorème fondamental de l'algèbre, tout polynôme de degré n à coefficients complexes admet n racines complexes, éventuellement multiples).

Factorisation sur  et .

 Sur  : les facteurs sont des polynômes de degré 1 (racines réelles) ou de degré 2 (sans racines réelles, mais éventuellement deux racines complexes conjuguées).

Sur  : tout polynôme peut être décomposé en produit de polynômes de degré 1 (facteurs linéaires), car les racines complexes sont prises en compte.

Cas des polynômes de degré 2.
Dans le cas d'un trinôme du second degré de la forme P(x) = ax² + bx + c, il est souvent utile de calculer la valeur de l'expression : Δ = b² - 4ac. Δ est appelé le discriminant du trinôme. La valeur de ce discriminant fournit des informations cruciales sur les racines du polynôme :

Si Δ > 0, le polynôme a deux racine réelles distinctes. 

Si Δ = 0, il n'y a qu' une seule racine réelle (une racine double). 

Si Δ < 0, il n'y a pas de racines réelles; les solutions sont deux nombres complexes conjugués. 

Dans le cas où Δ = 0, on aura donc : x1 = x2 = -/b/2a.

Exemple :

P(x) = x²− 5x + 6. Δ = b²−4ac = 1 >0 . Deux racines réelles : x¹ = 2x¹ ​= 2, x² = 3x²​ = 3.  P(x)=(x−2)(x−3)

Q(x)=x²+ x+1 : Δ = b² − 4ac= −3 <0. Deux racines complexes :

​​Sur  : Q(x) est irréductible.

Sur  :

Cas des polynômes de degré 3.
 Exemple 1 : P(x) = x³ − 6x² + 11x − 6. Méthode : chercher une racine évidente x1=1 (par P(1)=0). Factorisation par division :   P(x) = (x−1)(x²−5x+6).  Le second facteur se décompose encore :  P(x)=(x−1)(x−2)(x−3).

Exemple 2 : Q(x) = x³ + x² + x + 1. Racines complexes x=−1 (multiplicité 2) et x=−i, ou factorisation directe :  Q(x)=(x+1)²(x−i).

Cas des polynômes de degré 4.
Exemple : P(x) = x⁴−1. Utilisation de l'identité remarquable a²−b² = (a−b)(a+b) : P(x) = (x² − 1)(x² + 1) = (x−1)(x+1)(x²+1).

Sur , x² + 1 est irréductible.

Sur , x²+1=(x−i)(x+i), donc : P(x)=(x−1)(x+1)(x−i)(x+i).

Polynômes à coefficients réels et racines complexes.
Si un polynôme P(x) a des coefficients réels, ses racines complexes apparaissent toujours par paires conjuguées. Exemple : 

P(x)=x⁴+ x³+x²+x+1

Sur , il a les racines ω, ω², ω³, ω⁴ (racines 5^e de l'unité, où ω=e^2iπ/5).

Sur , il se factorise en : P(x)=(x² + x + 1)(x² − x + 1).

Chercher les racines évidentes ou par des méthodes comme Δ pour des degrés simples.

Utiliser la division polynomiale pour réduire le degré.

Continuer jusqu'à obtenir des facteurs irréductibles (selon le corps de coefficients,  ou ).