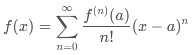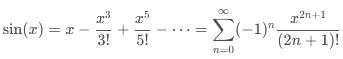-

La pensée et ses outils > Logique et théorie de la connaissance > Mathématiques > Analyse > Fonctions

La série de Taylor

La série de Taylor est une représentation d'une fonction (réelle ou complexe) en termes d'une somme de termes calculés à partir des dérivées de la fonction en un point a donné. Cela permet d'approximer des fonctions difficile à évaluer, mais facile à dériver, par des polynômes, qui sont beaucoup plus faciles à manipuler. Chaque terme du polynôme porte une partie de l'information sur la courbure de la fonction à travers ses dérivées. Cette série est nommée d'après le mathématicien britannique Brook Taylor, qui a formalisé cette idée au début du XVIII^e siècle.

Soit, par exemple une fonction f(x) qui est infiniment dérivable au voisinage de a, sa série de Taylor autour de a est :

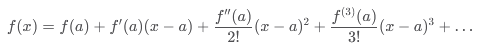Ou, de manière plus compacte :

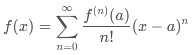
En principe, en prenant un nombre suffisamment grand de termes de la série, on peut obtenir une approximation aussi précise que nécessaire de la fonction dans un certain intervalle autour du point a. Mais, la série de Taylor ne converge pas nécessairement vers la fonction pour tous les points x, et la région où la série converge vers la fonction est appelée intervalle de convergence. La détermination de cet intervalle peut être un aspect important de l'analyse de la série. De plus, certaines fonctions ne peuvent pas être représentées exactement par une série de Taylor, soit parce qu'elles n'ont pas toutes les dérivées nécessaires, soit parce que leur série de Taylor ne converge pas vers la fonction en dehors du point a.

Une série de Taylor centrée en a = 0 est appelée série de MacLaurin. C'est un cas particulier de la série de Taylor.

Les séries de Taylor sont utilisées dans de nombreux domaines, comme l'approximation de fonctions, la résolution d'équations différentielles, l'analyse asymptotique, et bien d'autres.

Par exemple, la fonction exponentielle e^x a une série de Taylor très connue :

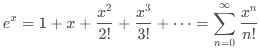
Cette série converge vers e^x pour tous les x réels et complexes.

De même, le sinus et le cosinus ont leurs séries de Taylor :

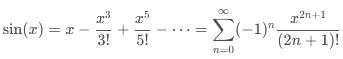
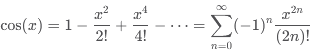
Ces séries sont particulièrement utiles en analyse numérique pour calculer des valeurs approchées de ces fonctions trigonométriques.

Dictionnaire Idées et méthodes