-

La pensée et ses outils > Logique et théorie de la connaissance > Mathématiques > Algèbre

La théorie de Galois

La théorie de Galois est une branche de l'algèbre qui traite de la relation entre les structures algébriques et les symétries de ces structures, et en particulier qui établit une connexion entre la théorie des groupes et la théorie des corps. Elle a été développée par Évariste Galois dans les années 1830, et elle fournit un outil puissant pour comprendre et résoudre les équations polynomiales. La théorie de Galois a révolutionné l'algèbre et a ouvert la voie à de nombreuses autres théories mathématiques, notamment en théorie des groupes, en géométrie algébrique, et en théorie des nombres. Elle a également des applications en cryptographie, en théorie des codes correcteurs d'erreurs et en physique théorique.

Le problème de la résolution d'équations polynomiales (trouver les racines d'un polynôme) est un problème central en mathématiques. Les équations du premier et du second degré ont des formules de résolution bien connues. Au XVI^e siècle, les formules pour les équations du troisième et du quatrième degré ont été découvertes. Cependant, les mathématiciens ont cherché en vain des formules générales pour les équations de degré supérieur à 4. La théorie de Galois apporte une réponse à cette question : elle détermine quand une équation polynomiale est résoluble par radicaux (c'est-à-dire, quand ses racines peuvent être exprimées à l'aide d'opérations arithmétiques et de racines n-ièmes).

Un corps est une structure algébrique qui généralise les nombres rationnels, réels et complexes. Il est muni de deux opérations (addition et multiplication) qui satisfont des propriétés similaires à celles des nombres usuels. La théorie de Galois utilise des extensions de corps : un corps E est une extension d'un corps F si F est un sous-corps de E. On note cela E/F.

Pour un polynôme donné, on peut considérer le corps de décomposition : le plus petit corps qui contient toutes les racines de ce polynôme.

Si un polynôme p(x) a des racines qui ne sont pas dans le corps de base F, on peut créer des extensions en adjoignant ces racines à F. Par exemple, si le polynôme x² + 1 n'a pas de racines dans le corps des nombres réels, on peut créer l'extension des nombres complexes en adjoignant i (tel que i² = -1).

Un automorphisme d'un corps E est une bijection de E sur lui-même qui préserve les opérations d'addition et de multiplication. Pour une extension E/F, on s'intéresse aux automorphismes de E qui laissent F invariant, c'est-à-dire qui ne changent pas les éléments de F. L'ensemble de ces automorphismes forme un groupe, appelé groupe de Galois de l'extension E/F, noté Gal(E/F). Ce groupe capture les symétries de l'extension de corps par rapport au corps de base.

Le coeur de la théorie de Galois est une correspondance biunivoque entre les sous-corps intermédiaires de l'extension E/F (les corps K tels que F 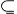K 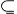E) et les sous-groupes du groupe de Galois Gal(E/F). Cette correspondance permet ainsi de relier les propriétés algébriques de l'extension de corps aux propriétés de symétrie du groupe de Galois. Elle est la clé pour comprendre la structure de l'extension de corps et résoudre le problème de la résolubilité par radicaux.

Le théorème fondamental de la théorie de Galois établit le lien suivant :

• Une équation polynomiale est résoluble par radicaux si et seulement si son groupe de Galois est un groupe résoluble.

Un groupe est dit résoluble s'il existe une suite finie de sous-groupes emboîtés, chacun étant distingué dans le suivant, telle que le quotient de deux sous-groupes successifs soit un groupe abélien.

La théorie de Galois permet de déterminer si les racines d'un polynôme peuvent être exprimées à l'aide de radicaux (racines carrées, cubiques, etc.). Par exemple, elle montre que les équations polynomiales de degré supérieur ou égal à 5 ne peuvent pas en général être résolues par radicaux, contrairement aux équations de degrés inférieurs.

Dictionnaire Idées et méthodes