Gnomon

Le gnomon était un instrument destiné à la détermination des hauteurs du Soleil et de la Luneau-dessus de l'horizon. Le gnomon des anciens se composait d'une tige verticale de longueur connue dressée sur un plan horizontal. On mesurait la longueur de l'ombre projetée par la tige, et, par une construction graphique, on déduisait la valeur de l'angle formé par le rayon lumineux avec le plan de l'horizon. Il est bien clair, d'ailleurs, que le rapport de la longueur du style à celle de l'ombre donne la tangente de l'angle cherché. Il convient de remarquer, tout d'abord, que le résultat obtenu était entaché d'une erreur égale au demi-diamètre de l'astre, car l'ombre mesurée se rapporte au bord supérieur de l'astre et non pas à son centre. 

La figure ci-dessous montre cet inconvénient sans qu'il soit besoin d'entrer dans aucune explication. Cette source d'erreur paraît avoir été connue de bonne heure; aussi, dans le but d'y remédier, donna-t-on au gnomon la forme d'un obélisque surmonté d'une boule. La longueur de l'ombre, prise depuis le centre de l'ombre de la boule jusqu'au pied de l'obélisque, se rapportait très sensiblement au centre de l'astre. Donc, pas de rectification à opérer.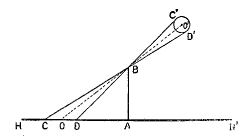 

On trouve cette disposition sur des médailles de l'époque de Philippe de Macédoine. Enfin, le gnomon permettait de déterminer assez exactement la direction de la ligne méridienne et, par suite, de la tracer sur le sol à partir du pied du style. Il suffisait pour cela de mesurer dans la même journée deux ombres d'égale longueur, circonstance qui se produit lorsque le Soleil occupe des positions symétriques par rapport au méridien. Cette méthode est d'une application plus rigoureuse, à l'époque des solstices, parce qu'à cet instant de l'année la variation de la déclinaison du Soleil est très faible (L'Année et les saisons). Ayant ainsi repéré, une fois pour toutes, la direction de la méridienne sur le sol, on pouvait prendre chaque jour la hauteur du Soleil en mesurant la longueur de l'ombre au moment où la pointe du style se projetait sur la ligne méridienne. 

Ératosthène construisit une sorte de gnomon connu sous le nom de scaphé, composé d'un style vertical dressé au fond d'une calotte sphérique creuse, de telle manière que la pointe coïncidait avec le centre de la sphère. L'ombre du style se projetait donc intérieurement sur la calotte sphérique; un cercle divisé d'égal diamètre s'appliquait à l'intérieur et donnait immédiatement l'angle formé par le rayon lumineux avec l'horizontale. On voit que cet appareil, s'il était d'un usage plus commode, comportait l'erreur d'un demi-diamètre signalée plus haut. La tradition a conservé le souvenir de gnomons de grande dimension. L'un fut établi à Rome à l'époque d'Auguste, dans le Champ de Mars, en utilisant dans ce but un obélisque de 105 pieds de hauteur rapporté d'Égypte; un autre de 165 pieds fut installé à Samarcande vers 1430.

Les savants du XVII^e et même du XVIII^e siècle remirent les gnomons en honneur, en les perfectionnant toutefois. Ils ne cherchèrent plus à mesurer l'ombre projetée par un style, mais, au contraire, ils déduisaient la hauteur du Soleil de la position de son image obtenue en laissant passer les rayons lumineux au travers d'une petite ouverture circulaire percée dans un mur élevé, à l'intérieur d'un édifice. Il est bien entendu que la distance de l'image était comptée depuis la projection sur le sol du centre de l'ouverture. On utilisait plus spécialement dans ce but les églises. Citons parmi les plus célèbres : le gnomon de l'église Santa Petrona à Bologne, installé par Cassini en 1655, dans lequel l'ouverture était située à 71 pieds au-dessus du sol; celui de l'église des Chartreux de Rome, réglé par Bianchini; celui de l'église Saint-Sulpice de Paris, organisé par Le Monnier; enfin, celui installé à l'observatoire de Paris en 1732, dans la grande salle du deuxième étage, par Cassini Il. Les cadrans du XVII^e et  du XVIIIe siècle, bien que beaucoup plus précis que ceux des anciens, puisqu'ils pouvaient donner à l'époque de leur installation les hauteurs méridiennes avec une approximation de 20" d'arc et les passages à 1 seconde de temps près, n'offrent guère qu'un intérêt historique, car depuis bien longtemps les instruments d'observation ont acquis une précision telle qu'il ne saurait être question d'utiliser les observations gnomoniques toujours douteuses, par suite des effets de tassement du sol ou des murs, postérieurs au tracé de la méridienne.

Ce qui fait que le gnomon ne peut servir, commodément au moins, à la détermination de l'heure, c'est que la variation incessante de la déclinaison du Soleil a pour effet de changer chaque jour la direction et la longueur de l'ombre du style sur le plan de l'horizon lorsque le Soleil traverse les mêmes plans horaires, c.-à-d. pour les mêmes intervalles de temps égaux avant ou après le passage au méridien aux différents jours de l'année. En effet, si z est la distance zénithale (Le repérage des astres) à un instant donné, AH l'angle horaire correspondant, A l'azimut de l'astre, D sa distance polaire, L la colatitude, la formule fondamentale (ci-dessous)  montre que pour des valeurs égales à AH, z varie si D varie :

Enfin, la formule suivante fait également voir que pour des valeurs égales de AH, A est différent si D n'est pas constant, comme il arrive au cours de l'année : :