Lorsqu'on considère les astres, on a affaire à de objets dont la position est définie dans un espace à trois dimensions. On a donc besoin de trois coordonnées pour définir leur position  (on peut même avoir besoin de six coordonnées, les trois coordonnées supplémentaires servant à définir la vitesse de l'astre). Cependant, avant avant d'avoir à dire où se trouve un astre (et quel est son déplacement dans l'espace), il faut commencer par dire où l'observer sur la sphère céleste. Toute fictive qu'elle soit, la sphère céleste possède comme toute sphère deux dimensions. Et donc ici encore deux coordonnées suffiront. 

Le principe est le même que celui utilisé pour repérer un point à la surface de la Terre. Ces coordonnées auront ainsi de grandes analogies avec la latitude et à la longitude qui servent à définir la position à la surface de la Terre; elles seront également rapportées à des grands cercles équivalents aux méridiens et aux parallèles utilisés pour notre globe. Simplement, la plupart du temps, ces différents  éléments auront d'autres noms, selon les choix qui seront faits pour les systèmes de coordonnées que l'on aura adoptés, c'est-à-dire pour les éléments de référence (plans et axes, directions, et autres conventions) auxquels on aura choisi de les rapporter. 

Les systèmes de repérage les plus souvent utilisés sont géocentriques (le centre supposé de la sphère céleste est le centre de la Terre) et locaux (le centre de la sphère céleste est l'observateur). On peut également recourir à des systèmes de repérage centrés sur le Soleil (systèmes héliocentriques) ou sur le centre de la Voie lactée (systèmes galactocentriques). Leur utilisation est fonction de contexte et des phénomènes que l'on étudie. Mais il convient de noter que tous souffrent d'un même inconvénient : les coordonnées que l'on peut y définir varient dans le temps, à des rythmes plus ou moins rapides. Les coordonnées locales, soumises à l'effet du mouvement diurne sont évidemment celles qui changent le plus vite. Les coordonnées équatoriales, qui sont des coordonnées géocentriques, utilisées dans les cartes célestes pour repérer les étoiles et les galaxies, subissent pour leur part l'effet de la précession des équinoxes, qui suit un cycle de près de 26 000 ans, etc. 

L'époque de référence* - Afin de tenir compte de la modification au fil du temps des coordonnées des astres du fait de la précession des équinoxes, ces coordonnées sont rapportées sur les cartes et les catalogues à une époque de référence. Le choix de la date a changé plusieurs fois dans le passé. Actuellement, on rapporte le plus souvent les coordonnées des astres aux valeurs qu'elles avaient (indépendamment de leur mouvement propre) le 1er janvier 2000 à midi (heure de Greenwich). Ce que l'on note conventionnellement J2000,0. Le J faisant référence à la période julienne, dans laquelle les années ont 365,25 jours.

Le terme géocentrique (du grec gè = Terre, et centron = centre) signifie qui a la Terre pour centre. Ainsi les systèmes de repérage géocentriques sont ceux qui font coïncider le centre de la sphère céleste avec le centre de la Terre. Ce choix laisse libre les autres éléments de références utilisés par le système de coordonnées choisis. 

Les éléments de référence.
Les trois premiers qui s'imposent sont l'équateur céleste, l'écliptique et le plan galactique (marqué par la trace de la Voie lactée dans le ciel), qui qui servent à définir respectivement, et en y jouant le même rôle, le système de coordonnées équatoriales, le système de coordonnées écliptiques et le système de coordonnées galactiques. 

L'équateur céleste*.
L'équateur céleste est le grand cercle de la sphère céleste, perpendiculaire à l'axe du monde, c'est à dire à l'axe de rotation de la Terre. Son intersection avec la Terre est l'équateur terrestre. Quant aux deux intersections de l'axe du monde avec la sphère céleste, ils constituent le pôle Nord céleste (près de l'étoile Polaire, dans la Petite Ourse) et le pôle Sud céleste (près de l'étoile Sigma de la constellation de l'Octant).

L'écliptique*. 
L'écliptique est la trajectoire apparente du Soleil au cours de l'année. Et par extension, c'est aussi le plan de l'orbite terrestre autour du Soleil. Comme la plupart des corps du Système solaire (à l'exception des comètes et des objets situés à sa périphérie) on des orbites proches de ce plan, on les trouve, sur la sphère céleste, toujours à l'intérieur d'une bande relativement étroite, centrée sur ce cercle, et recouverte par les douze constellations dites du zodiaque (ainsi que par Ophiuchus).

L'écliptique fait avec le plan de l'équateur terrestre (et donc avec l'équateur céleste) un angle de 23°27' environ, qu'on appelle l'obliquité de l'écliptique. 

La détermination de la valeur de l'obliquité de l'écliptique est l'un des plus anciens problèmes auxquels se sont confrontés les astronomes. Les premiers auteurs ont trouvé l'obliquité de l'écliptique de 24°; Ératosthène, 250 ans av. J.-C., de 23°50'; Albategnius, en 880, de 23° 35' 40"; Tycho Brahé, en 1587, de 23°31'30"; elle oscille aujourd'hui autour de 23° 23'. Euler et Laplace ont expliqué cette diminution par l'attraction mutuelle de toutes les planètes, dont les orbites, diversement inclinées, cherchent constamment à se confondre dans un même plan. Mais leur action (très puissante, puisque Vénus et Jupiter pourraient par leur attraction changer l'obliquité de l'écliptique de 10 à 20°) est combattue par la masse du Soleil. Delà, deux conséquences importantes que Laplace a déduites de ses calculs : l'une, que la variation de l'obliquité est périodique, de sorte que le Soleil, après s'être écarté de moins en moins de l'équateur, reviendra en sens contraire; l'autre, que l'obliquité ne pourra jamais varier que de 2 à 3 degrés.

La droite perpendiculaire au plan de l'écliptique et qui passe par le centre de la Terre intersecte la sphère céleste en deux points : le pôle Nord de l'écliptique (proche de la nébuleuse planétaire-NGC 6543 (l'Oeil de Chat), dans la constellation du Dragon), et le pôle Sud écliptique (dans la constellation de la Dorade, à proximité du Grand Nuage de Magellan). 

Les colures*. - On désigne ainsi deux grands cercles de la sphère céleste passant par les pôles célestes et par les points d'intersection de l'écliptique avec l'équateur céleste, et sont perpendiculaires à l'équateur. Ils sont aussi perpendiculaires l'un à l'autre; car ils se coupent tous deux à angles droits aux pôles du monde. L'un passe par les points équinoxiaux; c'est-à-dire qu'il coupe l'écliptique aux points où ce cercle est aussi coupé par l'équateur. On l'appelle, à cause de cela, colure des équinoxes. 

Le point vernal* - Le premier de ces points équinoxes, marque le début du printemps (dans l'hémisphère Nord), et il est appelé pour cette raison point vernal (du latin ver = printemps). 

L'autre passe par les points solsticiaux; c'est-à-dire, qu'il coupe l'écliptique aux points où ce cercle touche les tropiques. On l'appelle, pour cette raison, colure des solstices. Tous les astres placés sur le colure de solstices ont 90 degrés, ou 270 degrés d'ascension droite : et tous les astres placés sur le colure des équinoxes, ont 0, ou 180 degrés d'ascension droite.

La lignes des noeuds. - L'intersection de l'écliptique et du plan de l'orbite lunaire est la ligne des noeuds. De là la dénomination d'écliptique; car les éclipses ont lieu lorsque la Lune est voisine des noeuds, par conséquent voisine du plan de l'écliptique.

Le plan galactique.
Le plan galactique correspond au plan moyen de la Voie lactée. Son intersection sur la sphère céleste définit l'équateur galactique, et la direction perpendiculaire à ce plan indique celle des pôles galactiques. 

Les cercles horaires* -  Un cercle horaire est l'intersection avec la sphère céleste d'un plan qui passe par l'astre considéré et la ligne des pôles. C'est l'analogue d'un méridien sur le globe terrestre.

Les parallèles de latitude - Ces cercles de la sphère céleste sont analogues aux parallèles de la sphère terrestre. Dans le cas du système de coordonnées équatoriales, leur plan est perpendiculaire à l'axe du monde, et par conséquent parallèle au plan de l'équateur. Dans le cas du système de coordonnées écliptiques, leur plan est parallèle à l'écliptique.

Les coordonnées équatoriales*.
Si l'on veut fixer la position relative des étoiles sur la sphère céleste indépendamment du lieu et de l'heure de l'observation, il faut employer un système de coordonnées qui participe au mouvement diurne de la sphère céleste. On prend l'équateur céleste et le plan du méridien passant par le point vernal comme plans de référence, et on y rapporte l'étoile par deux coordonnées qui sont nommées déclinaison et ascension droite :

L'ascension droite*- C'est l'angle, noté a (alpha) ou AR (= Ascensio recta) que fait le cercle horaire d'un astre avec le cercle horaire du point vernal, intersection de l'écliptique et de l'équateur céleste. L'ascension droite se compte de l'ouest à l'est et de 0 à 360° ou de 0 h à 24 h. 

 
La déclinaison* - C'est la distance angulaire, notée d (delta), qui sépare un astre de l'équateur céleste. C'est dans le système de coordonnées équatoriales l'analogue de la latitude.  La déclinaison se compte de 0° à 90°; elle est boréale ou australe. 

Détermination de la déclinaison - La déclinaison est le complément de la distance polaire; il suffit par conséquent pour l'obtenir, d'observer, au moment où l'astre passe au méridien, la distance de cet astre au pôle.  On a observé préalablement une étoile circumpolaire à son passage supérieur et à son passage inférieur; la moyenne des nombres donnés dans ces deux cas par la graduation du cercle est le nombre qui répond à l'axe du monde; on note le nombre de la graduation du cercle auquel répond la direction de la lunette quand on observe l'astre dont on cherche la déclinaison; la différence entre ce nombre et celui qui répond à l'axe du monde, exprime la distance polaire de l'astre. Si elle est moindre que 90°, en en prenant le complément on obtient la déclinaison demandée, qui est alors boréale; si cette différence est plus grande que 90°, on en retranche 90°; le reste donne la déclinaison qui, dans ce cas, est australe. Lorsqu'il s'agit de la déclinaison d'un astre ayant un diamètre apparent comme le Soleil ou Lune, par exemple, il faut déterminer la distance polaire de son bord supérieur, celle de son bord inférieur, et prendre la moyenne pour avoir la distance polaire du centre, et par suite sa déclinaison. 

L'équatorial ou machine parallactique peut servir à mesurer par une seule observation la déclinaison et l'ascension droite d'un astre; mais il est ordinairement plus avantageux de déterminer séparément ces deux coordonnées, savoir : l'ascension droite par la lunette méridienne et la déclinaison par le cercle mural. Ces observations doivent être corrigées de la réfraction.

Les coordonnées écliptiques*.
Dans l'étude des mouvements du Soleil ou des planètes, on fait usage d'un autre système de coordonnées où le plan fondamental, au lieu d'être l'équateur céleste, est le plan de l'écliptique. Les deux coordonnées utilisées dans ce cas sont la latitude et la longitude écliptiques.

La latitude - Si, par une étoile, on mène un plan passant par l'axe de l'écliptique, la distance de l'étoile à l'écliptique, comptée sur ce cercle, est la latitude l ou l (Lambda);  La latitude se compte de 0 à 90° (soit de -90 à +90° entre les pôles écliptiques), elle est boréale ou australe; 

La longitude. La longitude b (Bêta) est l'arc compté sur l'écliptique, depuis le cercle de latitude jusqu'à l'équinoxe du printemps (le point vernal g); la longitude se compte, de l'ouest à l'est, de 0 à 180°, ou de 0 à 360°.

Angle de position, triangle de position. On appelle angle de position d'un astre l'angle formé à son centre par ses cercles de latitude et de déclinaison, on encore l'angle qui a pour sommet le centre de cet astre dans le triangle de position, ce triangle ayant lui-même ses trois sommets déterminés par l'astre, le pôle et le zénith du lieu d'observation.

Les coordonnées galactiques.
Le plan de référence est ici le plan galactique. La longitude l d'un point est comptée à partir de la direction du centre galactique (Sagittaire) et varie de 0 à 360° (l'anticentre - longitude galactique de 180° - se trouvant au sud de la constellation du Cocher, non loin de la limite avec le Taureau). La latitude b (comptée perpendiculairement au plan galactique) varie de 0° à + ou - 90°. 

Les régions les plus éloignées du plan galactique sont celles où la poussière interstellaire représente une gêne moindre pour l'observation. Aussi, c'est dans les directions proches des pôles galactiques (latitudes + ou - 90°) que l'on peut observer le plus facilement l'univers lointain. C'est par exemple dans des directions proches du pôle galactique nord, situé dans la constellation de la Chevelure de Bérénice que l'on peut observer divers amas de galaxies (Les grandes structures) tels que ceux de Coma (Chevelure de Bérénice) et de Virgo (Vierge). Le champ profond (nord) de Hubble, qui donne une vision de quelques uns des objets les plus lointains que l'on connaisse,  se situe également dans une direction proche, dans la constellation de la Grande Ourse. Pour sa part, le pôle galactique sud, situé dans la constellation du Sculpteur (non loin de l'amas globulaire NGC 288), donne accès dans son voisinage à certains autres champs riches en galaxies, à commencer par l'amas du Sculpteur.

Les repérages locaux.

En pratique, ce n'est évidemment pas depuis le centre de la Terre que sont conduites les observations astronomiques, mais généralement depuis sa surface. On fait alors comme si la sphère céleste était centrée sur l'observateur. La différence est négligeable quand il s'agit de fixer la position d'astres lointains (étoiles, galaxies). Elle peut être très importante quand on considère la position des corps du Système solaire. 

Nombre de techniques importantes ont d'ailleurs été élaborées dans le passé par les astronomes pour mettre à profit ce constat : déterminations des longitudes terrestres par l'observation de divers phénomènes (éclipses, occultations de satellites), détermination de parallaxes de divers corps du Système solaire (observations des passages de Vénus devant le disque solaire, notamment). 

L'horizon*.
Dans son acception première, l'horizon (du grec orizein, borner) est limite circulaire de la vue pour un observateur placé à petite distance de la surface de la Terre; c'est  l'endroit où se termine notre vue, où la Terre et le ciel semblent se toucher. Le mot désigne aussi l'étendue de la terre ou de la mer qu'on peut apercevoir en regardant autour de soi autant que la vue peut s'étendre.

L'horizon sensible - Dans un pays accidenté, la ligne d'horizon est sinueuse et irrégulière; mais quand on est au milieu des mers ou d'une vaste plaine, elle représente un cercle parfait. Ce cercle apparent est ce qu'on nomme l'horizon sensible, et l'on appelle horizon visible l'étendue de terre ou de mer comprise entre ce cercle et le lieu où se trouve l'observateur : l'horizon sensible divise le ciel en deux parties, l'une visible, l'autre qui ne l'est pas. 

L'horizon astronomique - Toutefois l'horizon sensible ainsi défini ne représente pas un plan horizontal, mais une surface conique, puisque l'oeil de l'observateur est situé à une certaine distance du sol. En pleine mer, lorsque l'oeil de l'observateur est seulement à 1,60 m de hauteur, le cône dont son oeil est le sommet va toucher la surface des eaux à plus de 4 500 m. Si l'oeil de l'observateur était placé à la surface même de la Terre, l'horizon serait un plan tangent à cette surface au lieu même de l'observation. Ce nouvel horizon, qui définit l'horizontale du lieu, et qui représente un plan tangent à la surface du lieu de l'observation, est ce qu'un nomme l'horizon rationnel ou horizon astronomique. C'est celui que l'on considérera ici. 

La dépression de l'horizon. - Horizon sensible et horizon astronomique font nécessairement entre eux un certain angle, lequel est d'autant plus grand que l'oeil de l'observateur est situé à une plus grande distance au-dessus du sol. Cet angle donne l'abaissement ou la dépression de l'horizon; il résulte de la forme sphérique de notre globe, et son observation fut le premier phénomène qui fit soupçonner la rotondité de la Terre aux astronomes de l'Antiquité.

L'horizon mathématique - Les astronomes admettent encore un troisième horizon, qu'ils appellent horizon mathématique, géométrique ou géocentrique, parce qu'il passe par le centre de la Terre. Ce nouvel horizon, qui divise exactement la sphère en deux hémisphères égaux, est parallèle à l'horizon rationnel. La distance entre ces deux horizons d'un même lieu est égale au rayon de la Terre. Les astronomes n'ont imaginé cet horizon géocentrique que pour rapporter toutes leurs observations au centre de notre globe. Lorsqu'il s'agit d'observations stellaires, ils prennent ces deux plans l'un pour l'autre, car une longueur de rayon terrestre est absolument insignifiante en raison de l'éloignement prodigieux des étoiles.

La verticale*.
On dit qu'une ligne droite est verticale lorsqu'elle est perpendiculaire au plan de l'horizon ou, ce qui revient au même, à la surface des eaux tranquilles. La verticale en un point se confond avec la direction de la pesanteur en ce point; comme elle, elle aboutit au centre de la Terre, et l'image en est donnée par le fil à plomb ou encore par la trace du centre de gravité d'une pierre qui tombe. 

Si l'on suppose la verticale qui passe par ce lieu prolongée indéfiniment, elle passera par le centre de la Terre, centre de l'horizon géocentrique, par le point de tangence de l'horizon rationnel, et par le sommet du cône de l'horizon sensible. Cette verticale sera donc l'axe commun de tous ces horizons, et elle ira rencontrer le ciel en deux points opposés. Le point qui se trouve au-dessus de l'observateur, c.-à-d. dans l'hémisphère visible, est appelé zénith, tandis qu'on appelle nadir celui qui est diamétralement opposé. Les deux mots sont empruntés à l'astronomie arabe : 

Le zénith* est le point de la sphère céleste où elle est rencontrée par la verticale du lieu. On l'appelle aussi pôle de l'horizon parce qu'il est éloigné de celui-ci de 90°. Le nadir est l'opposé du zénith. 

Le nadir* est la direction perpendiculaire au plan de l'horizon et diamétralement opposée à celle du zénith. Vers le bas, quoi.

Le méridien*.
Le méridien céleste est le grand cercle qui passe par la ligne des pôles et par la verticale du lieu considéré. Il divise en deux parties égales la sphère céleste ainsi que la courbe décrite par les astres dans leur mouvement apparent autour de la Terre, formant ainsi l'hémisphère oriental et l'hémisphère occidental. Le plan que définit ce cercle est le plan méridien. On peut se le représenter d'une manière familière par un grand carton vertical allant du Nord au Sud, et son intersection avec le plan de  l'horizon donne la méridienne. 

La méridienne* est l'intersection du plan méridien avec l'horizon. C'est une ligne qui va du Nord au Sud. Elle a été historiquement d'une  très grande importance. Voici les trois principales méthodes traditionnellement utilisées pour sa détermination. 

1° Par la boussole. La déclinaison magnétique étant occidentale à Paris et de 15°12' par exemple, si l'on prend une boussole de déclinaison munie d'une lunette, et si cette boussole est orientée, de manière à ce que l'aiguille aimantée soit dans la direction de 0-180°, comme la déclinaison de Paris est occidentale, on dirigera la lunette à 15°12' à l'Est, et cette lunette, étant assujettie à se mouvoir dans un plan vertical, permettra de jalonner une ligne en visant alternativement vers le Nord et vers le Sud, et donnera la méridienne.

2° Détermination de la méridienne par les hauteurs correspondantes du Soleil. Sur une table ou sur un terrain horizontal, on trace une ou plusieurs circonférence, au centre desquelles on place un gnomon ou une tige verticale qui porte ombre sur ces circonférences, d'abord avant midi, puis dans la soirée :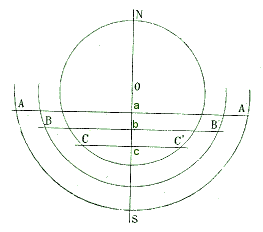 

Supposons que l'extrémité du gnomon ait son ombre en A vers neuf heures du matin et en A' vers trois heures du soir sur la même circonférence; comme le mouvement des astres est uniforme, le Soleil a mis le même temps pour passer de la position qu'il en,  ensuite employé pour aller de midi à la position qu'il occupait à trois heures de l'après-midi. Si donc du centre O n abaisse une perpendiculaire Oa sur la ligne AA', cette ligne Oa sera la méridienne. On répétera cette construction pour deux ou plusieurs autres circonférences qui seront rencontrées par l'ombre en B et B', C et C', et l'on obtiendra deux nouvelles directions Ob et Oc qui seront deux nouvelles méridiennes, que l'on trouvera confondues avec Oa. On aura donc ainsi la ligne Nord-Sud qui sera la méridienne géographique du lieu.

3° Détermination de la méridienne par la polaire. - Comme l'étoile polaire, celle de la Petite-Ourse n'est pas située exactement au pôle, mais bien à 1°15' du pôle environ, elle passe deux fois par jour au méridien et le rayon visuel mené à la polaire ne s'écarte jamais de la méridienne d'un angle supérieur à 1°15'. La Connaissance des Temps et l'Annuaire du Bureau des Longitudes permettent de trouver pour chaque jour de l'année les heures des passages de cet astre au méridien. On peut donc installer une lunette assujettie à se mouvoir dans un plan vertical, et viser l'étoile polaire avec cette lunette, que l'on abaisse ensuite jusqu'à un jalon qui se trouvera au Nord dans le méridien. On fait ensuite osciller cette lunette vers le S. et placer un second jalon qui se trouvera également dans le même plan. La ligne obtenue en joignant les deux jalons est donc la méridienne. On donne encore la méthode suivante : un premier fil à plomb étant fixé, un autre mobile, à un ou plusieurs mètres de distance, mais à peu près dans la direction de la méridienne, au commencement ou à la fin de la nuit, à l'heure du passage de la polaire au méridien, on déplace le second fil à plomb de manière que l'étoile polaire soit cachée par le plan des deux fils qui est lé plan méridien et la direction de ces deux fils donne la méridienne, déterminée fort exactement quand même il y aurait une erreur de quelques minutes dans l'évaluation du passage de l'étoile polaire. L'opération est beaucoup plus exacte quand on emploie la méthode des hauteurs correspondantes si l'on opère à l'époque des solstices. (L. Barré).

Le méridien géographique d'un lieu est le plan qui contient la verticale du lieu et qui passe par la ligne des pôles. 

Passage au méridien. - Moment où un astre rencontre le méridien. L'heure de ce passage au méridien, comptée en temps sidéral  qui marque 0h 0mn 0s quand le point vernal ou le point origine des ascensions droites passe au méridien, est l'ascension droite de l'astre. (L. B.).

Lorsque les seules techniques de la navigation astronomique étaient disponibles, l'observation de la hauteur des astres, planètes, étoiles au moment de leur passage au méridien, à l'aide du sextant, était d'un usage constant dans les calculs nautiques. On appelle premier méridien, un méridien de convention, dont le point de rencontre avec l'équateur terrestre forme le point de départ de la longitude. En France, on a longtemps adopté comme premier méridien celui de Paris, en Espagne celui de Tolède, en Suède celui d' Upsala, en Angleterre celui de Greenwich. C'est ce dernier qui désormais est adopté par tous. 
---

Les coordonnées horizontales*.
Le système de coordonnées horizontales constitue le système de coordonnées locales le plus utilisés.  Ses plans de référence sont l'horizontale du lieu d'observation et le plan méridien. On y défini la position d'un objet sur la voûte céleste par deux coordonnées, l'une est l'azimut a, l'autre la hauteur h. On remplace parfois la hauteur par l'angle complémentaire z = 90 - h, appelé distance zénithale. 

L'azimut* a (ou Az) est l'angle entre le cercle vertical passant par l'astre et le plan méridien. la mesure de l'azimut se fait de 0 à 360° à partir du Nord. Si l'objet est exactement au nord de l'observateur, son azimut sera nul. Il sera en revanche de 180°, s'il se trouve exactement au Sud. 

La hauteur* h est l'angle qui sépare l'astre du plan horizontal. Cet angle est mesuré selon la verticale de l'observateur. L'angle va de 0° à 90 de l'horizon au zénith et de 0° à -90° de l'horizon au nadir. Mais il faut encore distinguer la hauteur vraie de la hauteur apparente. Les astronomes appellent hauteur méridienne la hauteur d'un astre au moment où il passe au méridien; hauteur absolue, celle prise hors du méridien; et hauteurs correspondantes, deux hauteurs égales d'un même astre prises l'une à l'orient et l'autre à l'occident du méridien. 

A la hauteur de... - Dans le langage des marins, prendre la hauteur signifiait mesurer le degré de l'élévation du Soleil sur l'horizon, pour en déduire la latitude du lieu. Cette observation se faisait ordinairement à midi, lorsque le Soleil est dans le méridien du lieu de l'observation. De là est venue l'habitude de désigner la latitude sous le nom de hauteur, comme on dit :"nous étions à la hauteur des Açores, à la hauteur du cap Finistère, etc."

Les almicantarats (ou parallèles de hauteur) - On a donné ces noms à des cercles parallèles à l'horizon, qu'on imagine passer par chaque degré, par chaque minute et par chaque seconde du méridien, compris entre l'horizon et le zénith. Ces parallèles ont conséquemment leur pôle au zénith; ce sont eux qui déterminent la hauteur des astres : de sorte que tous les astres qui sont sous le même almincantarat ou le même parallèle de hauteur ont la même hauteur. 

La hauteur du pôle sur l'horizon est l'arc compris entre le pôle et le lieu de l'observateur la hauteur du pôle sur l'horizon d'un lieu n'est donc autre chose que la latitude de ce lieu. Quant à la hauteur de l'équateur, c'est également l'arc compris entre l'équateur et le point où se trouve l'observateur : elle est le complément de la hauteur du pôle. 

L'angle horaire* H est l'angle mesuré le long de l'équateur céleste entre le méridien local et le cercle horaire passant par cet astre. Cette mesure se fait à partir du Sud en tournant vers l'Ouest. Elle s'exprime le plus souvent en heures, minutes et secondes, mais parfois aussi en degrés (de 0° à 360°, dans le sens rétrograde).

 
La déclinaison* d, est, comme dans le système de coordonnées équatoriales, l'angle qui sépare un astre de l'équateur céleste. Ici encore, elle se mesure de 0° à 90° (positivement vers le nord et négativement vers le sud).

En librairie - Gianni Pascoli, Astronomie fondamentale, astronomie de position et mécanique céleste, Dunod, 2000. - André Caillemer et Catherine Le Cocq, Astronomie de position, géodésie, Technip, 1983.