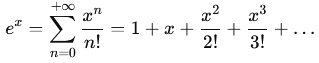La
fonction
exponentielle décrit une croissance ou une décroissance très rapide.
Son comportement de croissance rapide, sa simplicité de dérivation et
d'intégration, ainsi que sa présence dans de nombreux phénomènes naturels
et artificiels en font un outil indispensable dans de nombreux domaines
scientifiques et techniques. Elle se présente sous plusieurs formes. La
plus générale s'écrit f : x 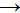 ax, ou a, appelée sa base, est un réel
non nul. Mais la plus courante est celle où la base est le nombre d'Euler
e. On parle alors d'exponentielle naturelle.
ax, ou a, appelée sa base, est un réel
non nul. Mais la plus courante est celle où la base est le nombre d'Euler
e. On parle alors d'exponentielle naturelle.
La fonction exponentielle
réelle
La fonction exponentielle
est définie par : expâ¡(x) = ex , où
e â 2,71828... est la base du logarithme naturel, appelée constante
ou nombre d'Euler. Elle associe à chaque réel x un réel strictement
positif.
Propriétés de
la fonction exponentielle.
Domaine
et image.
Le domaine de la
fonction exponentielle est l'ensemble de tous les nombres réels (-â
< x < +â).
L'image est l'ensemble
des nombres réels strictement positifs. La fonction ne prend jamais la
valeur 0 ou des valeurs négatives : autrement dit : expâ¡ : 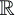 â â 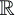 +*â;
l'image de la fonction est l'intervalle ]0,+â[. +*â;
l'image de la fonction est l'intervalle ]0,+â[.
Dérivée.
La fonction exponentielle
est égale à sa propre dérivée :
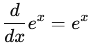
Primitive.
De même, sa primitive
est elle-même :
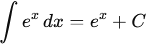
Valeur
en x = 0.
La valeur de la
fonction en x = 0 est 1 : e0 = 1.
Croissance.
La fonction exponentielle
est strictement croissante sur 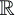 .
Plus x devient grand, plus ex grandit rapidement. .
Plus x devient grand, plus ex grandit rapidement.
Comportement
asymptotique.
Quand x tend
vers l'infini positif (x â +â), ex
tend également vers l'infini positif (ex
â +â). Quand x tend vers l'infini négatif (x â -â), ex
tend
vers 0 (ex â 0). L'axe des abscisses
(x) est une asymptote horizontale pour la fonction exponentielle quand
x tend vers -â.
Propriétés
algébriques.
La fonction exponentielle
suit les règles habituelles des exposants :
ea+b
=
ea.eb
eaâb
= ea / eb
(ea)b
= eab
Lien
avec les logarithmes.
La fonction réciproque
de ex est le logarithme naturel lnâ¡(x)
tel que :
lnâ¡(ex) = x et elnâ¡(x) =
x.
Lien
avec les séries.
La fonction exponentielle
peut être définie par le développement en série entière suivant :
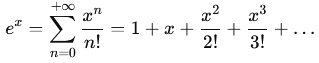
Cette série converge
pour tout réel x.
Représentation
graphique.
La courbe représentative
de ex reste toujours au-dessus de l'axe
des abscisses (strictement positive). Elle passe par le point (0,1) et
est strictement croissante.
La fonction exponentielle
et les équations différentielles.
La fonction exponentielle
intervientdans la résolution des équations différentielles linéaires,
qui apparaissent dans de nombreux domaines scientifiques comme la physique,
la biologie, l'économie ou l'ingénierie. Elle est la solution générale
de l'équation différentielle : yⲠ= ky, où k est une constante.
Ãquation
différentielle linéaire à coefficients constants.
L'une des formes
les plus courantes d'équation différentielle est :
yâ² = ky avec k 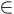 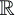 . .
où y est la
fonction inconnue dépendant d'une variable xx, yⲠreprésente la dérivée
de y et k est une constante réelle.
Résolution
de l'équation yâ²=ky.
Pour résoudre cette
équation, on cherche une solution de la forme y(x) = Cekx où
C est une constante à déterminer.
1) En dérivant
cette expression :
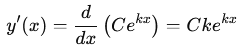 . .
2) En remplaçant
dans l'équation yⲠ= ky.
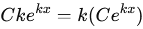
Cette égalité est
toujours vérifiée pour tout x, ce qui confirme que y(x)=Cekx
est
bien solution.
Exemple
de résolution avec condition initiale.
Considérons l'équation
différentielle suivante : yâ²=3y, avec la condition initiale y(0)=2.
La solution générale est y(x)=Ce3x. Pour
déterminer C, on utilise la condition initiale y(0)=2y(0)=2 : y(0)=Ce3.0
= C.1 = 2 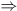 C=2. La
solution particulière est donc : y(x)=2e3x. C=2. La
solution particulière est donc : y(x)=2e3x.
Cas
d'une équation différentielle d'ordre supérieur.
Les équations différentielles
linéaires d'ordre supérieur font également intervenir la fonction exponentielle.
Exemple : équation
différentielle homogène d'ordre 2 :
Soit l'équation
: yâ²â²â4yâ²+4y = 0 (y" étant la dérivée seconde de y). On suppose
une solution de la forme y(x) = eλx où
λ est un paramètre à déterminer.
En dérivant
: yâ²(x) = λeλx , yâ²â²(x) = λ2eλx.
En remplaçant dans
l'équation : λ2eλxâ4λeλx+4eλx=0.
On factorise par eλx
(qui est toujours différent de 0) : λ2â4λ+4=0.
Résolvons l'équation
caractéristique : (λâ2)2 = 0 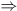 λ = 2.
λ = 2.
La solution générale
de l'équation différentielle est alors : y(x) = (C1+C2x)e2x,
où C1â et C2 sont
des constantes à déterminer à partir des conditions initiales.
Applications
dans les sciences.
Les équations différentielles
impliquant la fonction exponentielle modélisent une variété de phénomènes
dans les sciences :
⢠Croissance
exponentielle (biologie, économie). - Les modèles de croissance exponentielle
décrivent des phénomènes tels que la croissance des populations, les
intérêts composés ou l'accroissement des infections dans une épidémie.
yâ²=ky 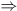 y(t) = y0ekt.
Si k > 0 : croissance (population, intérêts composés). Si k < 0 :
décroissance (radioactivité, refroidissement, élimination de médicaments
dans l'organisme), etc.. y(t) = y0ekt.
Si k > 0 : croissance (population, intérêts composés). Si k < 0 :
décroissance (radioactivité, refroidissement, élimination de médicaments
dans l'organisme), etc..
⢠Décroissance
radioactive (physique) . - La loi de désintégration radioactive est
donnée par : N(t)=N0.eâλt
où N0â est la quantité initiale et λ>0 est la
constante de désintégration.
⢠Circuit électrique
(RC). - Dans un circuit avec une résistance R et un condensateur C, la
charge q(t) du condensateur satisfait :

⢠Refroidissement
de Newton (thermodynamique). - La température d'un objet refroidissant
suit : T(t) = Tenv + (T0âTenv)eâkt,
où Tenvâ est la température ambiante.
La fonction exponentielle
complexe
La fonction
exponentielle complexe est une extension naturelle de la fonction exponentielle
réelle à l'ensemble 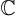 des nombres complexes et est intimement liée aux fonctions trigonométriques
grâce à la formule d'Euler. Elle
permet de décrire des rotations et des dilatations dans le plan complexe
et intervient en analyse complexe dans l'étude des fonctions analytiques.
des nombres complexes et est intimement liée aux fonctions trigonométriques
grâce à la formule d'Euler. Elle
permet de décrire des rotations et des dilatations dans le plan complexe
et intervient en analyse complexe dans l'étude des fonctions analytiques.
Définition de
l'exponentielle complexe.
Soit un nombre
complexe z défini par : z = x + iy,ou x 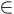 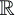 et y
et y 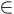 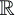 .
La fonction exponentielle complexe ez est
définie par la formule suivante : .
La fonction exponentielle complexe ez est
définie par la formule suivante :
ez
= ex+iy = ex.eiy
Ici :
⢠ex
est la partie réelle qui agit comme un facteur d'amplitude (un facteur
d'échelle),
⢠eiy
est la partie purement imaginaire, qui représente une rotation dans le
plan complexe.
Lien avec la trigonométrie
: formule d'Euler.
La partie eiy
est
donnée par la formule d'Euler : eiy =
cosâ¡(y) + isinâ¡(y), où cosâ¡(y) et sinâ¡(y) sont les fonctions trigonométriques
usuelles. Par conséquent, pour un nombre complexe z=x+iy, on obtient :
ez
= ex(cosâ¡(y) + i.sinâ¡(y)).
⢠Le terme
ex donne, ici encore, un facteur d'amplitude
(lié au module),
⢠Le terme cosâ¡(y)
+ i.sinâ¡(y) décrit une rotation d'angle y dans le plan complexe.
Représentation géométrique.
Dans le plan complexe,
ez représente une spirale logarithmique.
Le module de ez
est |ez| = ex.
L'argument de ez
est y.
Si x=0 (c'est-Ã -dire
z = iy), alors eiy représente une rotation
sur le cercle unité d'angle y.
Propriétés de
l'exponentielle complexe.
Continuité
et dérivation.
La fonction exponentielle
complexe est analytique sur 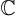 ,
et sa dérivée est donnée par ,
et sa dérivée est donnée par
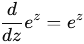
Multiplication
des exposants :
ez1+z2
= ez1.ez2 , 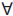 z1, z2
z1, z2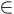 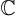 . .
Lien
avec les puissances et séries.
La fonction exponentielle
complexe est définie par sa série de Taylor
pour tout z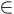 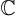 :
:
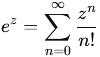
Exponentielle
purement imaginaire.
Si z=iy, alors :
eiy = cosâ¡(y) + i.sinâ¡(y). Autrement dit, l'exponentielle
purement imaginaire est une combinaison de rotations trigonométriques.
Exemple numérique.
Soit z = 1+iÏ.
Calculons ez :
1)
Appliquons la formule : ez = e1+iÏ = e1.eiÏ.
2) On sait que eiÏ
=
cosâ¡(Ï) + i.sinâ¡(Ï) = â1.
3) Donc : ez
= e1â
(â1) = âe.
|