 |
Le
terme variété est utilisé en mathématiques dans différents
contextes, mais il partage une idée commune : il s'agit d'un objet qui
est localement simple (généralement, ressemblant à un espace euclidien),
mais qui peut avoir une structure globale plus complexe.
Variété topologique.
La notion de variété
topologique est la plus fondamentale et celle sur laquelle les autres se
basent. Une variété topologique est un espace topologique qui ressemble
localement à un espace euclidien.
⢠Espace
topologique. - Un espace topologique est un ensemble muni d'une collection
d'ensembles appelés ouverts qui respectent certaines règles (l'union
d'ouverts est un ouvert, l'intersection finie d'ouverts est un ouvert,
l'ensemble vide et l'ensemble entier sont des ouverts).
⢠Localement
euclidien. - Pour chaque point de la variété, il existe un voisinage
de ce point qui est homéomorphe à un ouvert de l'espace euclidien 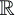 n
(où n est un entier positif appelé la dimension de la variété). Un
homéomorphisme
est une bijection continue dont la réciproque est également continue,
ce qui préserve la structure topologique. n
(où n est un entier positif appelé la dimension de la variété). Un
homéomorphisme
est une bijection continue dont la réciproque est également continue,
ce qui préserve la structure topologique.
Exemples de variétés
topologiques : l'espace euclidien 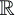 n
lui-même (est localement euclidien par définition), le cercle (S¹) (autour
de chaque point du cercle, vous pouvez trouver un petit arc qui ressemble
à un intervalle de n
lui-même (est localement euclidien par définition), le cercle (S¹) (autour
de chaque point du cercle, vous pouvez trouver un petit arc qui ressemble
à un intervalle de 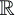 ¹),
la sphère (S²) (autour de chaque point de la sphère, vous pouvez trouver
une petite surface qui ressemble à un disque de ¹),
la sphère (S²) (autour de chaque point de la sphère, vous pouvez trouver
une petite surface qui ressemble à un disque de 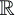 ²),
le tore, les grapphes des fonctions continues, etc.. ²),
le tore, les grapphes des fonctions continues, etc..
Ne sont pas des variétés
topologiques les espaces avec un point "pointu" ou une "arête": Par exemple,
un cône n'est pas une variété topologique car il n'est pas localement
euclidien au niveau de sa pointe. Même chose pour deux sphères qui se
touchent en un seul point. Ce point serait un problème.
Variété différentiable
(ou variété lisse).
Une variété différentiable
est une variété topologique avec une structure supplémentaire qui permet
de définir des notions de différentiation, de dérivation et de calcul
différentiel. Elle conduit à définir les notions suivantes :
â¢
Cartes
locales. - Pour chaque point de la variété, on a une carte (un homéomorphisme)
d'un voisinage du point vers un ouvert de 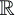 n. n.
⢠Transition
lisse. - Lorsque deux cartes se chevauchent, la transition entre elles
(c'est-à -dire la composée d'une carte et de l'inverse de l'autre) est
une fonction différentiable (de classe Cáµ, voire Câ).
Exemples de variétés
différentiables : tous les exemples de variétés topologiques mentionnés
ci-dessus, quand ils sont munis d'une structure différentiable adéquate
sont des variétes différentiables. Les surfaces dans 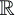 3
qui sont lisses. Les groupes de Lie (groupes
qui sont aussi des variétés différentiables). 3
qui sont lisses. Les groupes de Lie (groupes
qui sont aussi des variétés différentiables).
Variété algébrique.
Dans le cadre de
la géométrie algébrique, une variété algébrique est un ensemble de
points dans un espace affine ou projectif, qui est le lieu des zéros d'un
ensemble de polynômes. Ce sont des objets définis
par des équations polynomiales, par opposition aux structures lisses (fonctions
infiniment dérivables) des variétés différentielles.
Exemples de variétés
algébriques : les courbes et surfaces définies par des équations polynomiales
(par ex : paraboles, cercles, hyperboles, etc.); les grassmanniennes et
les variétés de drapeaux.
â¢
Une
grassmannienne est un espace qui paramètre les sous-espaces vectoriels
d'une dimension fixe dans un espace vectoriel donné. Plus précisément,
soit V un espace vectoriel de dimension n sur un corps K, et soit r un
entier positif inférieur ou égal à n. La grassmannienne Gr(r, V) est
l'ensemble des sous-espaces vectoriels de V de dimension r. La grassmannienne
Gr(r, V) peut être munie d'une structure de variété algébrique. Cette
structure est définie en utilisant les coordonnées de Plücker, qui sont
des fonctions polynomiales sur l'espace des sous-espaces vectoriels. Les
grassmanniennes sont notamment utilisées pour décrire les espaces de
modules de courbes algébriques, les espaces de configurations de particules
en physique et les espaces de données en informatique.
⢠Une variété
de drapeaux est un espace qui paramètre les suites de sous-espaces
vectoriels d'un espace vectoriel donné. Soit V un espace vectoriel de
dimension n sur un corps K, et soit (r1, ..., rk)
une suite d'entiers positifs tels que 0 ⤠r1
⤠... ⤠rk ⤠n . La variété de
drapeaux Fl(r1, ..., rk, V) est
l'ensemble des suites de sous-espaces vectoriels (V1,
... , Vk) tels que V1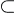 Vk et Vi = ri
pour tout i. La variété de drapeaux Fl(r1, ...,
rk, V) peut être munie d'une structure de variété
algébrique, définie ici encore en utilisant les coordonnées
de Plücker.
Vk et Vi = ri
pour tout i. La variété de drapeaux Fl(r1, ...,
rk, V) peut être munie d'une structure de variété
algébrique, définie ici encore en utilisant les coordonnées
de Plücker.
Autres
types de variétés.
Il existe d'autres
types de variétés, définies en fonction des structures supplémentaires
qu'on leur impose, comme par exemple :
â¢
Les variétés riemanniennes. - Variétés différentiables munies d'une
métrique Riemannienne qui permet de mesurer les distances et les angles.
⢠Les variétés
symplectiques. - Variétés différentiables munies d'une forme symplectique,
qui joue un rôle important en mécanique classique.
⢠Les variétés
complexes. - Analogue des variétés différentiables mais avec une structure
de nombres complexes.
|
|