-

La pensée et ses outils > Logique et théorie de la connaissance > Mathématiques > Analyse > Fonctions

Série et transformation de Fourier

Série de Fourier

Une série de Fourier est une manière de représenter une fonction périodique comme une somme infinie de fonctions trigonométriques (sinus et cosinus). L'idée centrale est qu'une fonction périodique f(t) peut être décomposée en une série de termes oscillants (sinus et cosinus) de différentes fréquences. Cette décomposition repose sur l'observation que les sinus et cosinus sont des fonctions orthogonales, ce qui permet de représenter n'importe quelle fonction périodique en termes de ces fonctions de base. Elle est nommée d'après Joseph Fourier, un mathématicien et physicien du XIX^e siècle, qui a étudié ce concept dans le cadre de son travail sur la propagation de la chaleur.

La série de Fourier d'une fonction f(t) périodique (de période T) est donnée par :

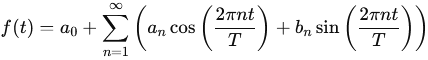
où a0 est le terme constant, représentant la moyenne de la fonction sur une période; an et bn sont les coefficients de Fourier, qui déterminent l'amplitude des termes cosinus et sinus pour chaque fréquence n.

Les coefficients a0, an, et bn sont obtenus en intégrant la fonction f(t) sur une période :

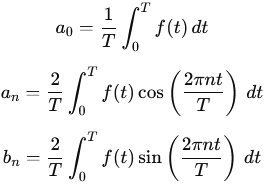
La convergence de la série de Fourier vers la fonction originale dépend des propriétés de cette dernière. Par exemple, si la fonction est continue et possède des dérivées continues, la série converge uniformément vers la fonction. Dans d'autres cas, elle peut converger au sens des moyennes ou presque partout.

Transformation de Fourier

La transformation de Fourier est un outil qui permet de convertir une fonction ou un signal du domaine temporel (ou spatial) au domaine fréquentiel. Contrairement aux séries de Fourier, qui décomposent les fonctions périodiques, la transformation de Fourier peut être appliquée à des fonctions non périodiques, en considérant ces fonctions comme périodiques avec une période tendant vers l'infini..

L'idée principale est que tout signal (ou fonction) peut être vu comme une somme infinie de fonctions sinusoïdales, ayant des fréquences, amplitudes et phases spécifiques. La transformation de Fourier exprime la contribution de chaque fréquence présente dans un signal.

Pour une fonction f(t) définie sur tout l’axe des réels (t 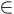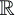), la transformation de Fourier F(ω) est donnée par :

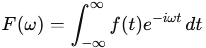
où F(ω) est la fonction dans le domaine fréquentiel; ω est la fréquence angulaire (en radians par seconde); e^−iωt est un terme complexe qui combine sinus et cosinus (par la formule d’Euler : e^iωt = cos⁡(ωt) −i.sin⁡(ωt)).

Transformation inverse.
La transformation inverse permet de revenir du domaine fréquentiel au domaine temporel :

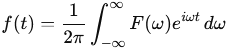Interprétation intuitive :

• Domaine temporel : le signal est décrit par ses variations en fonction du temps (ou de l’espace).
• Domaine fréquentiel : le signal est décomposé en ses composants en fonction de leurs fréquences. Chaque fréquence est associée à une amplitude (intensité) et une phase (décalage).

Applications.
La transformation de Fourier est utilisée dans une multitude de domaines :

• Traitement du signal : analyse audio (extraction de fréquences); compression de données (comme le MP3 ou JPEG); analyse des signaux radar ou biomédicaux (ECG, EEG).
• Physique : étude des vibrations et des ondes; diffraction et optique (théorie des ondes lumineuses);
• Résolution d’équations différentielles : conversion des équations dans le domaine fréquentiel pour les simplifier.
• Apprentissage automatique : extraction de caractéristiques dans des données complexes.
• Image processing : applications telles que les filtres pour améliorer ou transformer des images.

Variantes.

• Transformée de Fourier discrète (DFT). - La transformée de Fourier discrète est une version discrétisée de la transformation de Fourier. Elle s'applique à des signaux numériques échantillonnés (finis) au lieu de signaux continus. La DFT permet de passer du domaine temporel (ou spatial) au domaine fréquentiel pour des données discrètes. Avantages : calcul efficace grâce à l’algorithme FFT (Fast Fourier Transform), qui réduit le temps de calcul pour les grandes séries de données. Applications : traitement des signaux (analyse spectrale, compression MP3); analyse d'images (compression JPEG); résolution de systèmes dynamiques discrets.
• Transformée de Fourier à temps court (STFT). - La STFT (Short-Time Fourier Transform) est une adaptation de la transformée de Fourier qui permet d’analyser des signaux non stationnaires, c’est-à-dire des signaux dont les caractéristiques changent avec le temps. Elle découpe le signal en petites fenêtres temporelles et applique une transformée de Fourier à chaque fenêtre. Il existe un compromis temps-fréquence : une fenêtre large donne une bonne résolution fréquentielle mais une mauvaise résolution temporelle, et inversement. Applications : analyse audio (détection de changements dans le spectre); détection de défauts dans des signaux industriels; études biomédicales (EEG, ECG).
• Transformée en ondelettes. - La transformée en ondelettes est une méthode avancée qui surmonte certaines limites de la STFT. Elle décompose un signal en ondelettes, des fonctions localisées à la fois dans le temps et dans la fréquence. Contrairement à la STFT, la résolution varie : elle utilise des fenêtres étroites pour les hautes fréquences et larges pour les basses fréquences. Avantages : bonne résolution dans le temps pour les hautes fréquences; bonne résolution en fréquence pour les basses fréquences. Applications : compression et débruitage de signaux (ex. : images médicales); détection de transitoires ou d'événements rares dans des signaux (pannes, anomalies); analyse multirésolution en physique, traitement d’images, et géophysique.

Dictionnaire Idées et méthodes