 |
Lorsque dans une
série ou suite indéfinie de termes u0,
u1, l'un quelconque d'entre eux, un+p
peut s'exprimer en fonction des p qui le précèdent sous la
forme :
[1]
un+p =a1un+p+p-1
+ a2un+p+p-2
+ ... + apun
a1, a2...
ap étant des coefficients donnés
constants, on dit que cette suite est récurrente. La relation
[1] est appelée
relation de récurrence ou échelle de récurrence de
la suite, et celle-ci est dite de l'ordre p. Sous une forme symbolique,
la relation [1] peut
s'écrire :
un(up-a,
up-1 -...- ap)
= 0
et, si l'on pose :
f(x) = xp -
a, xp-1 -... - ap
la relation de récurrence devient
unf(u) = 0. L'échelle de récurrence
est alors f(u)=0, et peut être multipliée par un,
quel que soit l'entier n, toujours sous forme symbolique, les exposants
des lettres u devant être transformés en indices.
Une série récurrente du premier
ordre n'est autre qu'une progression par quotient, puisque un+1
= a1un,.
Une série récurrente d'ordre 2 est définie par :
un+2 =
a1un+1
+ 1 + a2un,
c.-à-d. que son échelle de
récurrence est :
f(u) = u2
- a1u - a2
= 0.
Toute suite récurrente d'ordre p
n'est complètement définie que si l'on donne ses p premiers
termes, en dehors de son échelle. Par exemple, la suite du 2e
ordre la plus
connue et la plus étudiée,
celle de Fibonacci, est définie par
ses deux premiers termes 0, 1, et par son échelle de récurrence
u2 - u - 1 = 0.. C'est donc 0, 1, 1, 2,
3, 5, 8, 13,...
Les suites récurrentes jouissent
de propriétés importantes et ont
fait l'objet de nombreux travaux. Elles intéressent à la
fois l'arithmétique et l'algèbre.
On peut les étendre aux quantités imaginaires.
Nous nous bornerons ici, à titre
d'exemple, à indiquer l'intéressante proposition que voici
: lorsque le rapport (un+1)/un
tend vers une limite, n augmentant indéfiniment, cette limite n'est
autre que la racine de plus grand module de l'équation f (x) =0,
f (u) = 0 étant l'échelle de récurrence. Ainsi, pour
la série de Fibonacci, l'échelle de récurrence conduit
à l'équation x2 - x - 1 =
0, dont les racines sont réelles, et la plus grande est :
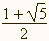 Il s'ensuit que les fractions 1/1, 2/1,
3/2, 5/3, 8/5, 13/8,... tendent vers :
Il s'ensuit que les fractions 1/1, 2/1,
3/2, 5/3, 8/5, 13/8,... tendent vers :
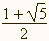 = 1,6180339..., un nombre connu sous le nom de nombre d'or.
= 1,6180339..., un nombre connu sous le nom de nombre d'or. |
|