Arbre de décision

Structure de l'arbre.
La structure d'un arbre de décision se compose de plusieurs éléments clés, organisés de manière hiérarchique. 

Noeud racine.
Le noeud racine est le point de départ de l'arbre de décision. Il représente la première décision ou question posée en fonction d'une caractéristique spécifique des données. Exemple : Dans un arbre pour classer des animaux, le noeud racine pourrait être "L'animal a-t-il des plumes?".

Noeuds internes.
Les noeuds internes sont les points de décision intermédiaires dans l'arbre. Chacun de ces noeuds pose une question basée sur une caractéristique des données. Chaque noeud interne a des branches qui représentent les différentes réponses possibles à la question posée. Chaque branche conduit à un autre noeud (interne ou feuille).  Exemple : Après "L'animal a-t-il des plumes?", un noeud interne pourrait poser la question "L'animal peut-il voler?"

Branches.
Les branches sont les chemins qui relient les noeuds entre eux. Elles représentent les résultats des tests effectués dans les noeuds. Exemple : Si la réponse à "L'animal a-t-il des plumes?" est "Oui", une branche pourrait mener au noeud suivant avec la question "L'animal peut-il voler ?".

Feuilles.
Les feuilles sont les noeuds terminaux de l'arbre, c'est-à-dire qu'ils ne mènent à aucun autre noeud. Chaque feuille représente un résultat final ou une décision basée sur les réponses aux questions précédentes. Exemple : Une feuille pourrait indiquer "L'animal est un oiseau" si toutes les conditions menant à cette feuille sont satisfaites.

Chemin. 
Un chemin est une séquence de branches allant du noeud racine à une feuille. Il représente la série de décisions prises pour arriver à une conclusion spécifique.  Exemple : Un chemin complet pourrait être "L'animal a-t-il des plumes?" → "Oui" → "L'animal peut-il voler?" → "Non" → "L'animal est un pingouin".

                             Schéma d'un arbre de décision (ultra-simplifié) :

                         [L'animal a-t-il des plumes ?]   ← Noeud racine
                             /                               \
                         Oui                            Non
                          /                                     \
       [L'animal peut-il voler ?]            [L'animal a-t-il des poils?]
              /                             \ 
            Oui                      Non                   ← Noeuds internes
           /                                   \
[L'animal est un oiseau]      [L'animal est un pingouin] ← Feuilles
 

Profondeur de l'arbre.
La profondeur de l'arbre est le nombre de noeuds depuis la racine jusqu'à la feuille la plus éloignée. Un arbre plus profond peut modéliser des décisions plus complexes, mais risque également de surajuster les données (overfitting).

Fonctionnement.
Le fonctionnement d'un arbre de décision consiste à prendre des décisions ou à faire des prédictions en passant par une série de tests sur les caractéristiques des données. 

Création de l'arbre de décision.
Le processus commence par la sélection de la caractéristique la plus discriminante pour être placée à la racine de l'arbre. Cette caractéristique est choisie en fonction de critères utilisés évaluer la qualité des divisions ou des scissions. Le jeu de données est ensuite divisé en sous-ensembles basés sur les valeurs de la caractéristique sélectionnée. Chaque sous-ensemble sera ensuite analysé de manière similaire dans les sous-noeuds. Le choix du critère dépend du type de données, du problème à résoudre et des objectifs spécifiques en termes de performance et d'interprétabilité, d'où divers modes de construction d'arbres de décision. Par exemple :

• Gain d'information (entropie). - L'entropie mesure l'incertitude ou le désordre dans un ensemble de données. Le gain d'information est la réduction de l'entropie obtenue après avoir divisé les données sur un attribut donné. L'objectif est de maximiser le gain d'information à chaque étape. 

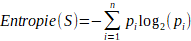
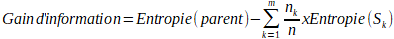
• Gain de Gini (indice de Gini pondéré). - L'indice de Gini mesure la qualité de la scission. Le gain de Gini mesure la réduction de l'impureté d'une distribution après une scission, et l'objectif est de minimiser l'indice de Gini pondéré. Cela signifie que la scission choisie maximise l'homogénéité des sous-ensembles par rapport à la variable cible. 

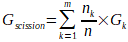
Gscission est l'indice de Gini de la scission, Gk est l'indice de Gini du sous ensemble k, nk est le nombre d'éléments dans le sous ensemble k, n est le nombre total d'éléments et m est le nombre de sous-ensembles résultants de la scission.

• Test du X². - Le test du X² (khi-deux) est utilisé pour évaluer si la distribution des classes dans les sous-ensembles obtenus après une scission est significativement différente de la distribution attendue. Une valeur élevée du test indique une bonne division.  χ² = ∑(O−E)² /E, où O est la fréquence observée et E est la fréquence attendue.

• Réduction de la variance (pour la régression). -  Utilisé dans les arbres de décision pour les tâches de régression, cette méthode cherche à réduire la variance des valeurs de la variable cible dans les sous-ensembles résultants d'une scission. L'objectif est de minimiser la somme des variances pondérées après chaque scission.

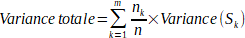
• Réduction de l'erreur de classification. - L'erreur de classification est  le pourcentage d'exemples mal classés dans un sous-ensemble. On cherche à réduire ce chiffre.  E(S)=1−max⁡(pi)  où pi​ est la proportion de la classe majoritaire. (Moins souvent utilisé car il est moins sensible que les au tres mesures, comme l'entropie ou l'indice de Gini, par exemple).

• Forêts aléatoires. - Les forêts aléatoires construisent plusieurs arbres de décision en utilisant des échantillons aléatoires du jeu de données (bagging) et en sélectionnant aléatoirement un sous-ensemble d'attributs à chaque noeud de chaque arbre. Cela introduit de la diversité dans les arbres et réduit le risque de surapprentissage.

• Boosting. - Dans le boosting, les arbres de décision sont construits séquentiellement, chaque nouvel arbre cherchant à corriger les erreurs commises par les arbres précédents. Les observations mal classées dans les arbres précédents sont pondérées davantage dans les arbres suivants.

• Arbres de décision obliques. - Contrairement aux arbres classiques qui utilisent des scissions perpendiculaires aux axes des caractéristiques (i.e., elles se basent sur un seul attribut à la fois), les arbres obliques utilisent des scissions linéaires qui combinent plusieurs attributs. Cela peut saisir des relations plus complexes entre les caractéristiques. Utilisé dans certaines variantes d'arbres pour la classification multi-dimensionnelle.

Arrivée aux feuilles.
L'algorithme s'arrête de créer de nouveaux noeuds quand l'une des conditions suivantes est remplie :

• Toutes les données dans un sous-ensemble appartiennent à la même classe (pour la classification).

• Aucune autre caractéristique n'est disponible pour la division.

• L'arbre a atteint une profondeur prédéfinie pour éviter le surajustement (overfitting).

• La feuille finale est assignée à la classe dominante dans ce sous-ensemble de données, ou à une valeur moyenne si c'est une tâche de régression.

Utilisation.
Les arbres de décision sont utilisés dans divers domaines pour la classification, la régression, la prise de décision, et même l'exploration de données :

Classification.
Un arbre de décision peut être utilisé pour classer des données en différentes catégories ou classes. Exemples : classer les patients en fonction de leurs symptômes pour prédire s'ils souffrent d'une certaine maladie; classer les emails comme étant du spam ou non en fonction de certaines caractéristiques comme le contenu, l'expéditeur, etc.

Régression.
Les arbres de décision peuvent également être utilisés pour la régression, c'est-à-dire pour prédire une valeur continue plutôt qu'une classe. Exemples : prédire le prix d'une maison en fonction de caractéristiques comme la superficie, le nombre de chambres, et l'emplacement; estimer la température ou les précipitations à partir de divers facteurs climatiques.

Prise de décision.
Les arbres de décision peuvent aider à prendre des décisions en entreprise en modélisant les différentes options et leurs conséquences. Exemples : évaluer les risques et les rendements attendus de différents projets d'investissement; décider quelles campagnes publicitaires lancer en fonction des données démographiques et des comportements des consommateurs.

Analyse prédictive.
Utiliser les arbres de décision pour prévoir des événements futurs ou des tendances en se basant sur des données historiques. Exemples : prédire les ventes futures en fonction des tendances passées et des facteurs saisonniers; identifier les clients susceptibles de quitter un service ou de résilier un abonnement en fonction de leur comportement.

Exploration de données (data mining).
Les arbres de décision peuvent être utilisés pour analyser et comprendre des ensembles de données complexes, en identifiant les relations et les patterns (motifs, régularités) cachés. Exemples : identifier différents segments de clients basés sur leurs comportements d'achat et d'autres caractéristiques; repérer les transactions suspectes ou les comportements frauduleux en analysant les données de transactions.

Systèmes de recommandation.
Utiliser des arbres de décision pour recommander des produits ou des contenus en fonction des préférences et du comportement des utilisateurs. Exemples : recommander des films à regarder en fonction des films précédemment visionnés et des évaluations données; suggérer des produits à acheter en fonction des articles déjà consultés ou achetés.

Planification et optimisation.
Les arbres de décision peuvent être utilisés pour optimiser des processus et planifier des ressources en évaluant différentes options. Exemples :  optimiser les chaînes de production en décidant quel produit fabriquer en fonction des demandes prévisionnelles; décider des meilleures routes de livraison en fonction des coûts, des temps de trajet et d'autres facteurs.