Parmi les plus anciens ouvrages connus on remarque le Zhoubi Suanjing (周髀算经) compilé à l'époque des Royaumes combattants (475-221 av. JC) qui contient des connaissances sur la géométrie et l'astronomie, incluant des méthodes pour calculer des distances astronomiques. Il contient en particulier des méthodes de calcul basées sur la mesure de l'ombre d'un gnomon (instrument utilisé pour déterminer la hauteur du soleil). 

Autre ouvrage, le Livre des Mutations (易经, Yìjīng), un texte classique. Bien qu'ésotérique, celui-ci utilise des concepts de numérologie et de symétrie qui influenceront la pensée mathématique chinoise. On y manipule, avec les trigrammes, la notion de permutation (Analyse combinatoire), mais sans la théoriser explicitement; on y trouve aussi une forme de numération binaire (sur la base du yin et du yang), mais qui est également très implicite. 

Dynastie Han (206 av. JC - 220 ap. JC)

A cette époque, les mathématiciens chinois utilisaient des bâtons de comptage pour représenter les nombres et effectuer des calculs arithmétiques. Cette méthode a permis de résoudre des problèmes complexes de manière pratique et efficace.

Les mathématiques étaient largement utilisées pour optimiser l'irrigation, la distribution des terres et la planification des cultures. Elles étaient appliquées à la construction de structures, de canaux et de routes. On recourait à des calculs complexes pour les échanges commerciaux (poids, mesures et conversions monétaires).

Les Neuf chapitres.
Les Neuf Chapitres sur l'art mathématique (九章算术, Jiǔzhāng Suànshù) est l'un des textes les plus influents de l'histoire des mathématiques chinoises. Il a été compilé progressivement entre le III^e siècle av. JC et le I^er siècle ap. JC. Contenu :

• 1 : Fangtian (方田, Mesure des champs). -  Introduction aux opérations arithmétiques de base : addition, soustraction, multiplication et division. Méthodes pour résoudre des problèmes impliquant des opérations arithmétiques : problèmes de division de terrains, de distribution équitable de ressources, etc. Calcul des aires de différentes formes géométriques, principalement pour l'agriculture.

• 2 : Sumi (粟米, Grain et céréales). - Problèmes d'arithmétique liés à l'agriculture et au commerce. Calculs de surface et de volume pour des formes géométriques simples telles que des rectangles, des cercles, des triangles, des parallélépipèdes, etc. Méthodes pour résoudre des problèmes pratiques impliquant des mesures de terrain, de construction, de stockage, etc.

• 3 : Cuihao (衰耗, Déchets et pertes). - Problèmes de proportions et de mélanges.

• 4 : Shaoguang (少广, Petit et grand). - Calculs de volumes et de proportions. Calculs des volumes des prismes, des cylindres et des pyramides

• 5 : Shangong (商功, Travaux de construction). - Problèmes d'ingénierie, incluant les volumes de divers solides.

• 6 : Junshu (均输, Répartition égale). - Distribution équitable de ressources et de travaux.

• 7 : Ying Buzu (盈不足, Excès et déficits). - Méthodes pour résoudre les équations linéaires à une ou plusieurs inconnues. Méthodes pour trouver des solutions aux problèmes impliquant des équations linéaires, souvent en utilisant des techniques d'équivalence, d'élimination ou de substitution.

• 8 : Fangcheng (方程, Équations). - Résolution de systèmes d'équations linéaires.  Des méthodes sophistiquées sont proposées, préfigurant des techniques modernes telles que celle par élimination de Gauss.

• 9 : Gougu (勾股, Le théorème de Gougu). - Problèmes de géométrie. Le théorème de Gougu, qui est l'équivalent du théorème de Pythagore, y est étudié au travers de ses applications.

Liu Hui  (刘徽) est un mathématicien du III^e siècle de l'ère commune. Il est l'auteur d'un commentaire détaillé des Neuf Chapitres. Il a amélioré et clarifié de nombreuses méthodes présentées dans les Neuf Chapitres et a proposé des méthodes plus rigoureuses et précises pour résoudre divers problèmes. Il propose  notamment une approche pour calculer le volume de solides, et on lui doit en outre une approximation de π. Il utilise pour cela une méthode basée sur les polygones inscrits et circonscrits. A partir de l'étude d'un polygone à 172 côtés il aboutit à une approximation de 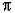égale à 3,14159. (Un peu plus tard, Zhu Chongzhi (429-500) parviendra pour sa part à l'encadrement 3,1415926 < 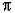 <3,1415927).

Le Classique de l'acupuncture et de la moxibustion.
Bien que principalement médical, le Classique de l'acupuncture et de la moxibustion (�'�灸甲乙经, Zhēn Jiǔ Jiǎ Yǐ Jīng) contient des concepts mathématiques utilisés pour les diagnostics et le traitement. Il utilise notamment des notions de symétrie.

Dynasties Sui et Tang (581-907)

Sunzi.
Le Sunzi Suanjing (孙子算经), attribué à Sunzi, a été compilé pendant la dynastie Wei du Nord (386-534). Il inclut des méthodes arithmétiques pratiques, comme la multiplication et la division, et la méthode de résolution des restes, qui est un précurseur du théorème chinois des restes. Ce théorème permet de résoudre des systèmes de congruences linéaires. Il est une des contributions importantes de Sunzi.

Wang Xiaotong.
Wang Xiaotong  (王孝通) est l'auteur du Jigu Suanjing (Continuation des classiques mathématiques). Il résout des équations cubiques de la forme x³+px²+qx=N, marquant une avancée significative dans l'algèbre.  Ses travaux concernent ar ailleurs  des solutions pour divers problèmes pratiques et théoriques.

Li Chunfen.
Li Chunfeng  (李淳风),  mathématicien et astronome, est connu pour ses contributions à la révision des classiques mathématiques. Il a édité et commenté plusieurs textes mathématiques classiques, et a ainsi contribué à leur préservation et à leur diffusion. Son travail en astronomie a influencé les calculs calendaires et les prédictions astronomiques.

Dynasties Song et Yuan (960-1368)

Jia Xian.
Jia Xian (贾宪) a été actif au XI^e siècle et a écrit sur les développements algébriques et les méthodes de calcul. Il a développé en particulier des méthodes pour extraire les racines carrées et cubiques, dont des mathématiciens ultérieurs comme Yang Hui sauront tirer profit.

Qin Jiushao.
Qin Jiushao (秦九韶) est un mathématicien du XIII^e siècle. Il est l'auteur du Shushu Jiuzhang ( 数书九章, Mathématiques en neuf chapitres) où il formalise l'utilisation théorème chinois des restes, permettant de résoudre des systèmes de congruences linéaires. Il a développ aussi des techniques pour résoudre des équations polynomiales de degré élevé et Qin traite de méthodes pour calculer les aires de figures complexes et les volumes de solides.

Yang Hui.
Yang Hui  (杨辉), actif lui aussi au XIII^e siècle, se signale par ses travaux en géométrie et pour la publication de plusieurs ouvrages mathématiques. On lui doit le triangle de Yang Hui, connu en Occident sous le nom de triangle de Pascal (un tableau triangulaire qui représente les coefficients binomiaux). Yang Hui a aussi travaillé sur des arrangements de nombres en carrés magiques. Il a également utilisé des diagrammes pour illustrer des problèmes géométriques et arithmétiques, facilitant la compréhension et l'enseignement des mathématiques.

Zhu Shijie.
Zhu Shijie (朱世杰, ca. 1280-1303) est l'un des plus grands mathématiciens de la dynastie Yuan. Il est, connu pour son Suanxue Qimeng (算学启�'�, Introduction aux mathématiques) et son Siyuan Yujian (四元玉鉴, Le miroir précieux des quatre éléments). Cet ouvrage contient un triangle de Yang Hui, mais où cette fois les coefficients du binôme sont disposés jusqu'à la puissance 8. Une méthode de résolution d'équations (jusqu'au 14^e degré) est également présentée. Elle est équivalente, mais antérieure de cinq siècles, à celle que proposera Horner. Zhu a développé en outre diverses méthodes pour résoudre des systèmes d'équations polynomiales à plusieurs variables, anticipant des concepts de l'algèbre moderne. Il s'est aussi intéressé aux carrés magiques et aux polyèdres, ainsi qu'à des applications pratiques de ces concepts.

Li Zhi.
Egalement connu sous le nom de Li Ye, Li Zhi  (李治) a travaillé sur les équations et les méthodes géométriques. Son Ceyuan Haijing (测圆海镜, Le miroir de la mer des mesures circulaires) contient des solutions géométriques pour des problèmes complexes. On y trouve en particulier une méthode pour résoudre des équations polynomiales en introduisant des variables inconnues (méthode de Tianyuan), ce qui est une avancée significative en algèbre. Ses travaux concernent aussi la recherche des solutions géométriques pour divers problèmes mathématiques et pratiques. 

Dynastie Ming (1368-1644)

Cheng Dawei.
Cheng Dawei (程大位, 1533-1606) est l'auteur d'un manuel mathématique intitulé Suanfa Tongzong (算法統宗, Compendium des méthodes de calcul), qui est une compilation exhaustive des techniques mathématiques chinoises, couvrant des sujets appartenant aussi bien à l'arithmétique, qu'à l'algèbre ou à la géométrie. L'ouvrage a été largement utilisé comme manuel d'enseignement.

Zhu Zaiyu.
Zhu Zaiyu (朱载堉, 1536-1611), également connu pour ses contributions en musique, a éa appliqué des principes mathématiques pour améliorer la théorie musicale, notamment en développant une division précise de l'octave en 12 intervalles égaux. Zhu a, par ailleurs, utilisé des méthodes numériques pour calculer les racines carrées et cubiques, anticipant des techniques modernes d'analyse numérique.

Les Jésuites et l'influence occidentale.
Les Jésuites ont dédaigné les avancées des mathématiques chinoises et se sont attachés à introduire en Chine les seules mathématiques qui valaient à leurs yeux, celles développées en Occident. Matteo Ricci (利玛窦), un missionnaire jésuite, a pu ainsi compter sur l'aide de  Xu Guangqi (徐光启, 1562-1633), un érudit chinois, pour introduire des concepts mathématiques occidentaux en Chine. Le Jihe Yuanben, traduction des Éléments d'Euclide a introduit la géométrie euclidienne en Chine,  et apporté une nouvelle perspective aux mathématiques chinoises traditionnelles.

Dynastie Qing (1644-1912)

Mei Wending.
Mei Wending (梅文鼎, 1633-1721) a travaillé à la fois sur les mathématiques classiques chinoises et sur l'intégration de concepts occidentaux. Il a édité et commenté de nombreux textes mathématiques classiques chinois, contribuant à leur préservation et à leur diffusion. Il a également amélioré les techniques de calcul et a travaillé sur des méthodes numériques avancées pour résoudre des problèmes arithmétiques et algébriques. Enfin, il a appliqué ses connaissances mathématiques à l'astronomie et à la révision des calendriers.

Dai Zhen.
Dai Zhen  (戴震, 1724-1777) est un érudit polyvalent dont les travaux en mathématiques ont apporté des contributions importantes à la géométrie et à l'arithmétique. Il a travaillé sur des méthodes pour calculer les aires et les volumes de formes géométriques complexes et a également abordé la  théorie des nombres, au travers des questions de congruence et de factorisation.

Li Shanlan.
Li Shanlan  (李善兰, 1811-1882) a accompli des efforts de synthèse entre les mathématiques chinoises et occidentales. Il a collaboré avec les missionnaires occidentaux pour traduire des œuvres mathématiques occidentales. Mais il a aussi travaillé sur les séries infinies et a abordé des concepts de calcul différentiel, utilisant des idées occidentales dans le cadre mathématique chinois.

Période moderne (depuis 1900)

Fondée en 1949, l'Académie chinoise des sciences a joué un rôle crucial dans le développement des mathématiques en Chine en fournissant un environnement propice à la recherche et à l'enseignement. Plusieurs instituts de recherche en mathématiques ont été créés à travers le pays, offrant des opportunités de recherche et de collaboration pour les mathématiciens chinois. Ceux-ci ont contribué à la résolution de problèmes classiques en théorie des nombres en développant de nouvelles méthodes algébriques et géométriques. Ils ont apporté des contributions significatives à la géométrie algébrique, en développant de nouvelles théories et en résolvant des conjectures célèbres. 

Parmi les mathématiciens chinois qui ont fait des contributions significatives au niveau international, on relève, par exemple, les noms de Hua Luogeng et de Chen Jingrun.
Hua Luogeng (1910-1985) est onsidéré comme le père des mathématiques modernes en Chine, il a apporté des contributions majeures à la théorie des nombres, à l'analyse fonctionnelle et à la géométrie. Chen Jingrun (1933-1996) est connu pour sa part pour son travail sur la conjecture de Goldbach. Il a fait des avancées importantes en théorie des nombres.

Les chercheurs chinois contemporains se sont également intéressés aux systèmes dynamiques complexes, étudiant les propriétés de la dynamique non linéaire et du chaos. Ils ont contribué à développer des techniques d'analyse avancées, notamment en analyse fonctionnelle et en théorie des opérateurs.

La Chine a mis en place un système d'éducation en mathématiques de haute qualité, produisant un grand nombre de diplômés en mathématiques chaque année.  Les étudiants chinois ont remporté de nombreux prix dans des compétitions mathématiques internationales. Plusieurs mathématiciens chinois ont remporté la Médaille Fields, l'une des plus hautes distinctions en mathématiques, démontrant le niveau élevé de recherche mathématique en Chine.