Leibniz montre ce rare exemple d'un génie dont la vocation pour les mathématiques ne s'est révélée qu'assez tard et qui a fait néanmoins dans ce domaine des découvertes capitales, tout en étant loin de s'y adonner complètement. Si dès l'âge de vingt ans, il avait écrit une dissertation, De Arte cornbinatoria (intéressante, mais contenant diverses erreurs), si cinq ans après il commençait à exposer ses idées sur le mouvement et entrait, à cette occasion, en relations avec Oldenbourg à Londres, avec Honoré Fabry à Rome, il savait en réalité encore assez peu de mathématiques quand il vint à Paris, en 1672, et y refit son éducation (il dit lui-même qu'alors Descartes lui paraissait obscur). Sa principale préoccupation paraît avoir été de bonne heure (en dehors de la construction d'une machine à calculer) la combinaison de nouveaux algorithmes pour faciliter la langue des calculs, peut-être pour constituer la science universelle qu'il rêvait dès 1663. Si c'est précisément dans cet ordre d'idées qu'il créa l'algorithme du calcul différentiel et du calcul intégral, il fit plusieurs essais semblables qui n'aboutirent pas. 

Ainsi le t. V de l'édition de ses oeuvres mathématiques par Gerhardt contient (pp. 141-171) une Characteristica geometrica, qui a pour but l'exposition d'un système de notations destiné à faciliter les raisonnements en géométrie. Leibniz le communiqua en 1679 à Huygens; mais, découragé par l'avis peu favorable de ce dernier, ne le publia pas. Le premier résultat important qu'il obtint fut le développement de 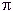 (Pi), suivant la série déjà trouvée par Gregory, mais non publiée. Il y arriva dès 1674, rédigea un traité qui fut prêt pour l'impression en 1676, mais que ses autres découvertes lui firent négliger, et il ne reprit l'exposition de ses travaux sur les séries qu'en 1682, dans les Acta eruditorum de Leipzig. Dans son traité primitif, il avait déjà fait la première application connue des indices; en 1693, il enseigne au marquis de L'Hôpital l'emploi de deux indices et en montre l'utilité pour les éliminations au moyen d'un algorithme qui se rapproche singulièrement de celui des déterminants. 

L'invention des signes du calcul différentiel et intégral est des mois d'octobre et novembre 1675 (les papiers de Leibniz, publiés par Gerhardt, sont heureusement datés); la première est celle du signe, qu'il employa quelque temps sans indiquer la différentielle; il désigna d'abord celle-ci par x/d, au lieu de la notation dx, qu'il finit par adopter. Il appliquait les signes pour retrouver les résultats déjà obtenus on exposés par Cavalieri, Grégoire de Saint-Vincent, Pascal, qu'il raconte lui-même avoir été ses maîtres par leurs livres, tandis qu'il ne fait aucune mention des Lectiones de Barrow, où l'on a voulu retrouver les sources de ses idées. En 1676, le 24 juillet, Oldenbourg, interrogé par lui sur les développements de sin x et arcsin x, qu'il avait su avoir été obtenus en Angleterre, lui apprend que ces résultats sont dus à Gregory; que, d'autre part, Newton lui a communiqué, en 1672, une méthode générale des tangentes et que cette méthode rentre dans une autre s'étendant aux quadratures, etc. 

Newton envoyait en même temps à Leibniz sa série du binôme, divers autres développements, mais sans preuves et rien de plus. En répondant, Leibniz laissa entendre qu'il était lui-même en possession du moyen de résoudre le problème inverse des tangentes. Il fit vers la même époque un court voyage à Londres (le second), où Collins lui communiqua le traité manuscrit de Newton, De Resolutione aequationum affectarum. Enfin le 24 octobre 1676, Newton écrivit à Leibniz une seconde lettre, où il développa son invention du binôme, et, pour s'assurer la priorité de son calcul des fluxions, inséra un anagramme, qui n'aurait certainement renseigné en rien Leibniz, s'il avait pu le déchiffrer. Le savant allemand répondit aussitôt après la réception de la lettre par une claire exposition de sa méthode des tangentes avec l'algorithme différentiel, montra comment il pouvait ainsi traiter le problème inverse (intégral) et exprima la conjecture que la méthode de Newton ne devait différer de la sienne. Newton, qui ne voulait pas publier sa méthode, encore trop imparfaite à ses yeux, ne répondit rien. Leibniz, de son côté, attendit jusqu'en 1682 pour faire connaître dans les Acta Eruditorum qu'il possédait une méthode particulière pour les problèmes de maximis et minimis, et en 1684 pour exposer dans le même recueil cette Nova Methodus. 

Dès 1685, Craig vulgarisa en Angleterre la découverte de Leibniz, qui s'était ainsi assuré la priorité de la publication, tandis que celle de l'invention d'une nouvelle méthode est due sans conteste à Newton, qui ne fit connaître qu'en 1686, dans son immortel livre des Principes, les fondements du calcul des fluxions et encore ne les exposa que synthétiquement (la première exposition réelle du calcul des fluxions fut donnée par Wallis en 1693, dans son Algèbre, d'après des lettres de Newton). La même année (1686), Leibniz développait ses découvertes dans deux nouveaux Mémoires des Acta Eruditorum; le second, De Geometria recondita, est de beaucoup le plus important, surtout au point de vue du calcul intégral. Newton, dans un scholie de la première édition des Principes, avait reconnu l'indépendance de l'invention de Leibniz tout en réservant ses propres droits. Dans la seconde édition (1743), ce scholie subit une légère modification, destinée à bien marquer la différence des deux méthodes. Dans la troisième (1726), il est remplacé par un autre, où il n'est plus parlé de Leibniz et où Newton attribue à ses communications à Collins (dont Leibniz avait pu avoir connaissance) une importance qu'elles étaient loin d'avoir. 

Pendant ce temps, Leibniz se créait une école; les Bernoulli, L'Hôpital en France apprenaient à se servir de sa méthode, et surtout les premiers rivalisaient bientôt avec le maître; mais ce dernier continuait à produire de brillantes applications de ses procédés, à la solution du problème des courbes isochrones (1689), à la conception des coordonnées curvilignes et des enveloppes, à la voûte quarrable de Viviani  (1692), à l'emploi des séries pour l'intégration des équations différentielles, à la tractrice (1693), à la brachistochrone (1697), etc. Cependant, ses relations avec les savants anglais se refroidissaient; le rôle politique important de Leibniz et son action jusqu'en Angleterre, dans le sens whig (Tories et Whigs),  en faveur de la ligne hanovrienne, déplaisaient aux torys et à Newton comme tel. 

Dès 1699, un esprit inquiet, Fatio de Duillier, se mettait à contester les droits de Leibniz à son invention. Cette attaque n'aurait probablement pas en de suite, si le savant allemand avait pu venir s'entendre franchement à Londres avec son rival de gloire. En tout cas, la querelle n'éclata qu'en 1704, à la suite d'un compte rendu dans les Acta Eruditorum de la dissertation de Newton sur les quadratures. Outré d'une violente attaque de Keill dans les Philosophical Transactions, Leibniz soumit la question à la Société royale de Londres. Une commission, nommée pour l'examiner, conclut, sur le rapport de Halley, à la publication d'une série de lettres de Newton, Barrow, Gregory, Leibniz, etc. C'est le Commercium epistolicum de 1712 (réédité en 1722, puis en 1856 par Biot et Lefort) qui est une oeuvre de parti et dont Leibniz se plaignit hautement; mais sa mort l'empêcha de présenter sa défense, et nombre d'assertions erronées ont, à la suite, eu cours sur l'histoire de la découverte des nouveaux calculs jusqu'à ce que la connaissance des originaux tronqués dans la première édition du Commercium, modifiés dans la seconde, et la publication des papiers de Leibniz aient permis, au XIX^e siècle, de rétablir la vérité. On ne peut que déplorer que Newton, sans se montrer, ait permis et même guidé contre son rival des attaques dont il connaissait pertinemment la fausseté; on doit peut-être regretter encore plus que Leibniz qui, de fait, avait le beau rôle, ait essayé, dans diverses de ses lettres, de pallier certains détails qu'il pouvait hautement avouer. (P. Tannery).