-

Cotes

Roger Cotes est un mathématicien né en 1682 à Burbach, dans le comté de Leicester, mort à Cambridge le 5 juin 1716. Son père, membre de l'Eglise anglicane, le destina d'abord au sacerdoce, mais le laissa bientôt suivre le penchant décidé qui l'entraînait vers les sciences et que l'un de ses parents le mit à même de cultiver. Dès 1706, il était choisi, à l'âge de vingt-quatre ans, pour occuper une chaire d'astronomie et de philosophie expérimentale que venait de fonder Thomas Plume à l'université de Cambridge.Tout en poursuivant ses travaux scientifiques, il continuait cependant, suivant le désir de son père, l'étude des langues et de la théologie, se faisait recevoir docteur de cette dernière faculté et entrait dans les ordres en 1713.

Sa mort prématurée ne lui permit que de publier, en dehors d'une seconde édition (1713) des Principia de Newton, pour laquelle il composa une remarquable préface, seulement deux mémoires qui furent insérés dans les Transactions philosophiques; le premier est un traité d'analyse intitulé Logometria; le second contient la description d'un météore observé en Angleterre, le 6 mars 1716. Pour qu'il se décidât à faire paraître son premier travail, il avait d'ailleurs fallu les vives instances d'un de ses amis, le docteur Bentley. Mais il laissait en manuscrit de plus importantes recherches; elles furent réunies par un autre de ses amis, Robert Smith, qui lui succéda dans sa chaire et les fit paraître sous le titre : Harmonia mensurarum sive Analysis et Synthesis per rationum et angulorum mensuras promota : accedunt alia opuscula mathematica (Cambridge,1722, in-4). Il publia également (Londres, 1737 et 1747) des Lectures de Cotes sur l'hydrostatique et la pneumatique. Ces deux ouvrages ont été traduits en français, le premier assez librement et avec des développements dus au bénédictin anglais Walmsley : l'Analyse des mesures, des rapports et des angles ou réduction des intégrations aux logarithmes et aux arcs de cercle (Paris, 1747); le second, par Lemonnier, sous le titre : Leçons de physique expérimentale sur l'équilibre des liqueurs (Paris, 1740). Le plus bel éloge de Cotes est dans le mot célèbre de Newton-:

« Si Cotes avait vécu, nous saurions quelque chose. »

Il fut prononcé à l'occasion de recherches sur l'optique que le jeune mathématicien avait commencées avant sa mort. On doit dès lors être d'autant plus surpris du pamphlet : Epistola ad amicum de Cotesii inventis, qui parut anonyme à Londres à la suite de la publication de l'Harmonia mensurarum et où l'on s'attache à réduire les inventions de Cotes à de simples déductions des théories de Newton. Il est certainement fâcheux pour l'illustre inventeur du calcul des fluxions qu'il ait eu des amis trop jaloux de sa gloire, non seulement vis-à-vis des étrangers, comme Leibniz, mais encore vis-à-vis de ses compatriotes : car si Cotes procède évidemment de Newton, s'il doit même sans aucun doute être considéré comme un de ses disciples, il n'en est pas moins réellement indépendant et l'idée mère qu'il a développée se retrouverait plutôt dans lés écrits antérieurs de Leibniz et de Jean Bernoulli que dans ceux de Newton. Cette idée mère se trouve au reste condensée dans l'énoncé du théorème auquel on a conservé le nom Cotes. (P. T.).

Théorème de Cotes. - Si, dans un cercle de rayon a, décrit sur un diamètre AB, on divise, à partir de l'origine A, cotée O, la circonférence en un nombre pair 2m de parties égales, aux points cotés 1, 2,... 2m-1; si de plus, on prend sur le diamètre un point O, (à une distance x quelconque, comptée du centre vers A) et qu'on le joigne à tous les points de division, le produit de toutes les droites menées aux numéros impairs est égal à x^m+a^m et le produit de toutes les droites menées aux numéros pairs est égal à x^m -a^m.
Si, en effet, on prend la droite menée de O au point de division coté n, il est aisé de voir que : [On]² = x² - 2ax Cos (n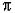/m) + a², et l'on reconnaît dès lors facilement que l'énoncé ci-dessus correspond à la solution complète de l'équation binôme, si l'on fait le produit des facteurs imaginaires conjugués au premier degré.
En d'autres termes, le théorème de Cotes représente la première forme donnée à la théorie développée plus tard par Moivre, tandis que l'origine première en remonte évidemment aux découvertes de Viète sur les sections angulaires. D'ailleurs, en partant de ce théorème, Cotes a obtenu l'intégration des fractions rationnelles ayant pour dénominateur x^m ± a^m; il a donc fait faire un pas décisif au calcul intégral, et l'on ne peut guère douter que, si sa vie se fût prolongée, il n'eût dignement rivalisé avec les Bernoulli.

Francis Cotes est un peintre anglais, né à Londres en 1726, mort à Londres le 20 juillet 1770. Elève de G. Knapton, il devint bientôt célèbre par ses portraits au crayon, au pastel et à l'huile. Membre de l'Incorporated Society of Artists, il fut l'un des fondateurs de l'Académie royale.

Brillant coloriste, il sut donner à ses portraits une vivacité d'expression et un charme vraiment remarquables. On peut citer parmi ses meilleurs ouvrages, le portrait de la Reine Charlotte, tenant la princesse royale sur ses genoux (1767, gravé par Rowland); à l'Académie royale, le portrait du Père de l'artiste, et à l'hôpital de Greenwich, le portrait en pied de l'Amiral Hawkes. (Ad. T.).

Samuel Cotes est un peintre né à Londres en 1734, mort à Londres le 7 mars 1818. Frère cadet du précédent. Il peignit en miniature, sur émail et sur ivoire, et fit des portraits au crayon. Son habileté ne tarda pas à le faire classer parmi les premiers artistes de son époque, et il exposa régulièrement des miniatures à l'Académie royale, à partir de la seconde exposition de cette société en 1769. Lorsqu'il mourut, il avait cessé de peindre depuis longtemps. (Ad. T.).

Dictionnaire biographique