Moivre

Après la révocation de l'édit de Nantes, il se réfugia en Angleterre, où il vécut comme professeur de mathématiques, se fit remarquer de Newton et de Halley et fut admis en 1697 à la Royal Society puis à l'Académie des sciences de Paris, et fut un des commissaires chargés de prononcer entre Leibniz et Newton au sujet de l'invention du calcul intégral. 

Moivre s'est surtout occupé du calcul des probabilités. Outre de nombreux mémoires insérés dans les Philosophical Transactions, il a laissé : The Doctrine of chances (1716, 1738, 1756); Annuities on lives (1724, 1742, 1750); Miscellanea analytica de seriebus et quadraturis (1730, in-4).  C'est dans ce dernier ouvrage que se trouve la formule connue sous son nom.

Théorème de Moivre. - Si i représente l'unité imaginaire 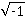 on a : (cos a + i=.sin a) (cos b + i.sin b)... = cos (a + b +...) + i.sin (a+b + ...). C'est cette identité qui constitue le théorème de Moivre, ou la formule de Moivre, l'une des plus fécondes propositions de l'analyse. Elle, donne en particulier, si on suppose a = b = ... : (cos a + i.sin a)^m = cos ma + i.sin ma, et c'est surtout cette dernière forme dont on a l'occasion de faire usage. C'est la formule de Moivre qui a conduit Euler à identifier cos a + i.sin a avec l'exponentielle imaginaire e^ia, et à donner au cosinus et au sinus les expressions bien connues : cos a = (e^ia + e^-ia)/2,  sin a = (e^ia - e^-ia)/2i.