Un arc-en-ciel.

Certaines  caractéristiques de l'arc-en-ciel (couleurs visibles, largeur) dépendent de la taille des gouttes d'eau impliquées. Mais d'autres sont constantes. Le centre de l'arc-en-ciel est ainsi toujours le même : si l'on suppose des rayons visuels autant de l'oeil du spectateur et aboutissant aux divers points de l'arc, l'ensemble de ces rayons constitue un cône circulaire droit dont le demi-angle au sommet, toujours le même, est de 40° environ. Le sommet de l'arc se trouve donc à une distance de 180° - 40° =  140° du Soleil, cette distance étant comptée sur l'arc du grand cercle céleste passant à la fois par le sommet de l'arc et par le Soleil. En fait, on observe souvent deux arcs : l'arc intérieur ou principal, que l'on vient d'évoquer, est celui dont les couleurs sont les plus vives et les plus pures; le violet s'y montre sur la frange interne, le rouge à l'extérieur. La disposition inverse s'observe dans l'arc extérieur ou secondaire,  d'un diamètre apparent un peu plus grand (correspondant à 52° environ), qui manque souvent et est toujours plus pâle. Parfois des arcs dit surnuméraires encore plus pâles et dans lesquels on remarque surtout le rouge et le vert, sont également observables, en particulier près le bord interne du premier arc. Ils sont dus à des phénomènes d'interférences, comparables à ceux qui sont responsables des irisations observées sur les nuages. 

La théorie explique l'existence de ces deux arcs et même celle d'un plus grand nombre, bien que dans la nature on n'ait pas eu lieu d'observer d'arc d'ordre supérieur au troisième; mais on a pu, dans des expériences disposées convenablement, vérifier les conclusions de la théorie et observer jusqu'à quatorze arcs concentriques. 

L'arc-en-ciel marin.
L'arc-en-ciel marin paraît assez souvent lorsque la mer est extrêmement agitée, et que le vent, soulevant ses vagues, fait que les rayons du Soleil qui tombent sur leur surface, se réfractent et y peignent les mêmes couleurs que dans les gouttes de pluie ordinaires. Les couleurs de l'arc-en-ciel marin sont cependant moins vives, moins distinctes, et de moindre durée que celles de l'arc-en-ciel ordinaire. En général, on y distingue à peine plus de deux couleurs : du jaune du côté du Soleil, et un vert pâle du côté opposé. 

L'arc-en-ciel par réflexion.
Quand les rayons solaires se réfléchissent à la surface d'un lac, ils semblent partir d'une image du Soleil symétrique de cet astre par rapport au plan de la surface de l'eau. Ces rayons sont capables, comme les rayons directs, de donner lieu au phénomène de l'arc-en-ciel : ils produisent des arcs de même diamètre, ayant les mêmes couleurs que les autres, ils ont pour centre un point situé sur la droite qui joint l'oeil de l'observateur à l'image du Soleil; ils sont plus élevés que les arcs directs qu'ils coupent souvent. Aux points d'intersection on n'aperçoit quelquefois que de la lumière blanche, par suite de la recombinaison des couleurs. Les sommets des arcs formés par les rayons réfléchis s'écartent d'autant plus des autres que le Soleil est plus élevé au-dessus de l'horizon. Les marins sont assez souvent témoins de ce phénomène. 
-

Arc-en-ciel par réflexion. Gravure tirée de Meteorological Optics, de
Pernter (1906). En médaillon : une photographie de M. Zscharnack.
(Source : Atmospheric Phenomena Page; © Matthias Zscharnack, Dresde).

L'arc-en-Terre.
Quand le Soleil est assez haut au-dessus de l'horizon on aperçoit quelquefois un arc-en-ciel se projetant sur terre (on l'appelle alors un arc-en-terre) et dû à des gouttelettes de rosée. Le phénomène est le même et l'arc se trouvant à la fois sur le cône visuel dont nous avons parlé et sur l'herbe a l'apparence d'une section conique, ellipse, parabole ou branche d'hyperbole selon la hauteur du Soleil au-dessus de l'horizon. Lorsque cette hauteur est plus grande que la déviation des rayons efficaces, soit 40° pour les rayons violets, la section du cône est une ellipse. Pour 40°, c'est une parabole; si la hauteur du Soleil est plus petite on apercevra une hyperbole, c'est le cas le plus fréquent parce que la rosée nécessaire à la production du phénomène disparaît en général avant que le Soleil ait atteint la hauteur de 40°. 

Le cercle-en-ciel, l'arc-en-ciel inversé.
Quand le Soleil est assez élevé au-dessus de l'horizon, les arcs dus à la réflexion des rayons solaires peuvent former des cercles complets (cercles-en-ciel); il arrive parfois que la partie supérieure de ces cercles manque, de sorte que l'on aperçoit un arc-en-ciel renversé. 
-

Une curiosité, le cercle-en-ciel ou arc-en-ciel circulaire.
(Source : Mountain Light, © Galen & Barbara Rowell).

L'arc-en-ciel lunaire.
Beaucoup plus rare et bien moins spectaculaire, l'arc-en-ciel lunaire est pour le reste similaire à l'arc-en-ciel solaire. C'est un arc coloré qui ne se présente à l'observateur qui tourne le dos à la Lune, lorsqu'il a devant lui un endroit où il pleut. Comme la cause de ce phénomène est la même que celle de l'arc-en-ciel solaire, on comprend qu'il soit beaucoup plus faible, du fait du peu d'intensité de la lumière que la Lune nous renvoie; aussi paraît-il ordinairement blanchâtre, et très peu d'auteurs disent y avoir distingué une ou deux couleurs. Ou voit aussi que c'est au moment de l'opposition de la Lune avec le Soleil (pleine lune), qu'on un doit le plus espérer de l'apercevoir, parce qu'alors la Lune est le plus brillante. 

Aristote dit qu'on ne l'avait pas remarqué avant lui, et qu'on ne l'aperçoit qu'à la pleine Lune. Sa lumière dans d'autres temps est trop faible pour frapper la vue après deux réfractions réfractions et une réflexion. Ce philosophe nous apprend qu'on vit paraître de son temps un arc-en-ciel lunaire dont les couleurs étaient blanches. Gemma Frisius dit aussi qu'il en a vu un coloré; ce qui est encore confirmé par Verdries, et par Sennert qui en a observé un semblable en 1599. Snellius dit en avoir vu deux en deux ans, et R. Plot en a remarqué un en 1675; en 1771, on en signala un, dans la province de Darbyshire en Angleterre. Thoresby qui a donné la description d'un arc-en-ciel lunaire dans des Transactions Philosophiques n° 331, dit que cet arc était admirable par la beauté et l'éclat de ses couleurs; il dura environ 10 minutes, après quoi un nuage en déroba la vue. Weidler a observé, en 1719, un arc-en-ciel lunaire, lorsque la Lune était à demi-pleine, dans un temps calme, où il pleuvait un peu : mais à peine put-il reconnaître les couleurs; les supérieures étaient un peu plus distinctes que les inférieures; l'arc disparut aussitôt que la pluie vint à cesser. Musschenbroëck dit en avoir observé un le premier d'octobre 1729, vers les 10 heures du soir : il pleuvait très fort à l'endroit où il voyait l'arc-en-ciel : mais il ne pu distinguer aucune couleur, quoique, précisait-il, la Lune eût alors beaucoup d'éclat. Le même, auteur rapporte que, le 27 août 1736, à la même heure, on vit à Yffelstein un grand arc-en-ciel lunaire, très éclatant; mais cet arc-en-ciel n'était partout que de couleur jaune. (Brisson).
-
Arc-en-ciel double.  A noter, la trace d'arc surnuméraire visible à droite 
de l'arc intérieur, ainsi que l'obscurcissement de la zone située entre les
deux arcs principaux, déjà décrit par Alexandre d'Aphrodisie, et  qui
porte le nom de bande sombre d'Alexandre. (Source : Site d'Andrew Revering).

Les philosophes de l'Antiquité se sont préoccupés de l'explication du phénomène de l'arc-en-ciel; ils ont remarqué tout d'abord, d'après les positions relatives de l'arc, de l'observateur et du Soleil, qu'il devait y avoir réflexion de la lumière, telle est la seule idée exacte qu'ils ont eu de ce météore. Malgré les études ultérieures, il faudra le début du XVII^esiècle pour que soit découverte la cause du phénomène, et qu'on en propose une théorie qui, pour l'essentiel, peut encore être retenue aujourd'hui. 
-

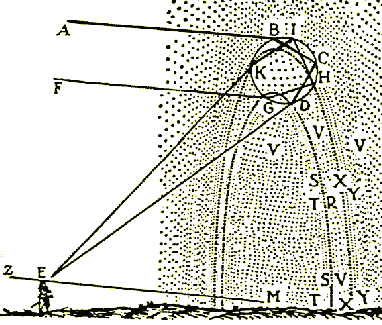
La théorie de l'arc-en-ciel dans le Traité des Météores de Descartes.

Aristote 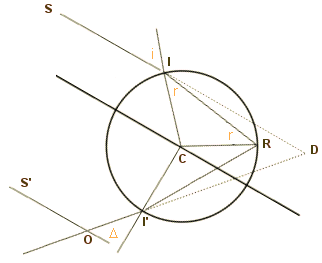supposait que la réflexion a lieu sur la surface convexe des gouttes d'eau; Posidonius et Sénèque pensaient que le nuage formait miroir sphérique concave. Maurolycus (1494-1575) paraît être le premier qui ait observé la constance du diamètre apparent de l'arc, chercha à l'expliquer en admettant la réflexion à la fois sur la partie extérieure et convexe et sur la partie intérieure et concave de la goutte d'eau. Vitellus fit faire un pas de plus à la question en remarquant que, puisqu'il y avait coloration, il devait y avoir réfraction et dispersion par suite; mais à cette époque les lois de la dispersion étaient mal connues et c'est ce qui empêcha Kepler de donner une explication plus précise du phénomène, comme on le voit par les lettres qu'il écrivit à Béranger en 1605 et à Harriot en 1606.; cependant il indiqua la vraie marche du rayon qui pénètre dans la goutte en se réfractant, éprouve la réflexion totale, puis sort en se réfractant de nouveau. Antonio de Dominis, archevêque de Spalatro (Split), est le premier qui ait tenté d'expliquer le phénomène de l'arc-en-ciel par une réflexion de la lumière à l'intérieur des gouttes de pluie, dans son traité De radiis visus el lucis (Venise, 1611). Il réussit assez bien la théorie du premier arc-en-ciel, mais il se trompe complètement pour le second; en 1637, dans le huitième discours de son Traité des météores, Descartes qui a suivi l'explication de Dominis, a corrigé celle de l'arc extérieur; mais, comme ces deux auteurs n'entendaient pas l'origine des couleurs, l'explication qu'ils ont donnée de ce météore est défectueuse à quelques égards. Newton, complétant les travaux de Descartes, donna enfin la théorie élémentaire.

Les paramètres de la théorie.

Considérons une goutte d'eau de centre C et des rayons solaires parallèles SI, SO. Supposons l'observateur placé en O. Le rayon lumineux rencontrant la goutte d'eau tombe en un point I, il se réfracte en ce point en suivant la direction IR, en R il éprouve la réflexion totale et se dirige suivant RI', symétrique de RI, par rapport au rayon CR; en I' il sort en se réfractant de nouveau et prenant la direction I'O symétrique de IS, par rapport au même rayon CR. L'oeil aperçoit donc la rayon venant du Soleil suivant SI dans la direction OI'; appelons D (Delta) l'angle que fait cette direction avec la direction S'O des rayons solaires. Remarquons que de tous les rayons parallèles à SI qui tombent sur la goutte d'eau, seul le rayon SI arrive dans l'oeil après réfractions et réflexion, ou plutôt, comme l'oeil n'est pas un point unique, un pinceau lumineux très étroit, ayant pour axe SI, pénètre seul dans l'oeil par l'ouverture de la pupille, après la marche qui vient d'être indiquée. Mais si la goutte d'eau considérée fait voir le rayon SI dans une direction OD, faisant un angle D avec la direction S'O du Soleil, une autre goutte, située plus bas ou plus haut, plus près ou plus loin, va renvoyer les rayons du Soleil dans une direction faisant un angle autre que D, de sorte qu'il semblerait tout d'abord que chaque goutte doit donner un arc-en-ciel et que tous ces arcs élémentaires se superposant les uns les autres devraient produire du blanc; mais il n'en est rien parce que leur éclat est très différent selon leur position, de sorte que, parmi tous les rayons, certains seulement sont efficaces. Pour le comprendre, supposons tout d'abord que le rayon solaire soit d'une seule couleur, le rouge, par exemple; tous les rayons solaires tombant sur la goutte d'eau la rencontrent suivant des angles différents, y pénètrent et sortent suivant des angles qui sont de même différents. Nous appellerons déviation du rayon solaire l'angle que fait le rayon solaire incident avec le rayon émergent. Cette déviation est différente pour les divers rayons solaires que frappent la goutte d'eau : elle varie depuis 180° jusqu'à une valeur minima qui est de 42° pour les rayons rouges et de 40° pour les rayons violets.

Il suit de là que si les rayons solaires étaient rouges et si la voûte céleste ne nous renvoyait pas par diffusion la lumière du Soleil, alors on apercevrait dans le ciel un disque coloré en rouge; ce serait la base d'un cône ayant notre oeil pour sommet et 42° pour angle. Ce disque aurait-il une teinte uniforme? non, et c'est là le point important, car tous les rayons solaires tombant sur la goutte d'eau y sont dispersés et distribués d'une façon inégale. L'intensité de la coloration serait beaucoup plus vive sur les bords parce que ces points correspondent au minimum de la déviation et que l'on sait qu'au voisinage d'un minimum les fonctions varient peu pour des valeurs assez différentes de la variable; il en résulte que les rayons solaires qui rencontrent la goutte d'eau sous un angle assez voisin de celui qui correspond au minimum de déviation ont leur image très voisine du bord du disque, tandis que des rayons solaires très voisins entre eux, mais rencontrant la goutte d'eau sous un angle un peu différent de l'incidence correspondront au minimum, sont fortement déviés; il passe donc, pour ainsi dire, beaucoup plus de rayons sur les bords du disque que sur tout le reste de sa surface, les bords sont donc bien plus vivement éclairés. Au lieu de nous placer dans le cas où la lumière du Soleil ne contiendrait que des rayons rouges, plaçons-nous dans celui où il ne nous enverrait que des rayons violets. Tout ce qui vient d'être dit s'appliquerait encore, mais le disque violet, concentrique au premier, au lieu de correspondre à un angle de 42°, ne correspondrait qu'à un angle de 40°. Pour les autres couleurs, les angles correspondants seraient intermédiaires. Que va-t-il arriver si nous supposons, ce qui est le cas réel, que la lumière solaire contient toutes les couleurs. Au lieu d'un seul disque nous en aurons une série, le plus large sera de 42°, le plus étroit de 40°. Ces disques concentriques empiéteront les uns sur les autres et leur couleurs se combineront pour former du blanc presque partout, parce qu'elles auront une intensité sensiblement égale; mais pas sur les bords, parce que le bord du jaune, par exemple, qui correspond à 41° environ, contient du jaune, de l'orangé et du rouge, mais avec des intensités très différentes, le jaune possédant en cet endroit son éclat maximum, qui n'est atteint pour l'orangé et le rouge que par des angles un peu plus grands; le jaune dominera donc. Nous aurons ainsi une série de cercles concentriques où le violet, l'indigo, le bleu, le vert, le jaune, l'orangé et le rouge domineront successivement, nous aurons l'arc-en-ciel.

Cette théorie explique seulement la présence de l'arc primaire; mais on peut montrer l'existence, non seulement d'un second arc, mais même d'un nombre quelconque d'arcs. Supposons, en effet, un rayon lumineux éprouvant non plus une réflexion totale, mais bien deux, ou en général un nombre quelconque à l'intérieur de la goutte d'eau, on pourra avoir de cette façon autant d'arcs que l'on considérera de réflexions successives, le premier arc correspondant à une réflexion, le second à deux et ainsi de suite; mais les arcs successifs seront de plus en plus difficiles à observer et ils ne pourront être visibles que dans des cas particuliers que l'on n'a pas rencontrés encore dans la nature, soit que la grosseur des gouttes de pluie soit trop faible en général, soit que l'illumination du ciel sur le fond duquel se détachent les arcs-en-ciel soit trop forte pour qu'on puisse distinguer les moins éclairés. Au contraire, dans des expériences de laboratoire Babinet a pu apercevoir 14 et Billet jusqu'à 19 arcs, dont les positions correspondaient bien à celles quels théorie leur assignait. 

Les premières expériences sur ce sujet sont dues à Robant, élève de Descartes : il suspendait dans une chambre noire un ballon de verre mince rempli d'eau.

On faisait tomber sur cette sphère un petit faisceau de rayons lumineux et l'on plaçait l'oeil de côté, de façon que la droite allant de l'oeil à la sphère fit un angle de 42° environ avec la direction du faisceau lumineux employé; on apercevait alors, en déplaçant légèrement l'oeil, successivement, toutes les parties de l'arc-en-ciel. On pouvait aussi recevoir les rayons lumineux sur un écran percé d'un trou à travers lequel passait le faisceau lumineux. Si l'on employait de l'eau un peu trouble on pouvait suivre la trace de la lumière à l'intérieur de l'eau par suite de l'illumination des particules solides contenues dans l'eau qui se trouvaient sur le parcours des rayons solaires.

Babinet a repris ces expériences avec des cylindres de verre et il a pu distinguer les rayons efficaces après quatorze réflexions successives; il a aussi employé un let liquide cylindrique pour ces expériences. Billet a pu aller encore plus loin et apercevoir dix-sept arcs. Précisons cependant que ces arcs ne correspondent pas aux arcs surnuméraires effectivement observés. Pour comprendre l'origine  interférentielle de ces arcs, il faudra attendre le début du XIX^e. Pemberton, contemporain de Newton, l'avait soupçonnée, mais, après qu'aient été émises diverses autres théories, comme celle de Venturi, ce sont Young, en 1804, puis Arago et Babinet qui en feront la théorie, puis Airy, qui a fourni une solution analytique du problème (Trans. of the Society of Cambridge, VI, p. 379).  Elle est très compliquée, mais elle explique parfaitement les arcs surnuméraires observés dans les arcs-en-ciel, comme l'ont montré les expériences qu'elle a inspirées à Miller. 

Il n'a pas été tenu compte dans tout ce qui précède de la grosseur des gouttes de pluie; dès qu'elles atteignent un certain diamètre, dépassé la plupart du temps dans les pluies ordinaires, elles produisent les phénomènes de l'arc-en-ciel; les gouttes très petites produisent, au contraire, des phénomènes de diffraction dont les effets se superposent à ceux de la réfraction. ils sont responsables des arcs surnuméraires. (Joannis, Kaemtz).--