-

La pensée et ses outils > Philosophie > Métaphysique / Mathématiques

Infini

Le fini et l'infini en philosophie

En philosophie, le mot fini exprime l'idée d'une chose qui a des limites; ainsi, toute figure est limitée ou finie dans l'espace, toute durée est limitée dans le temps. Tout ce que perçoivent les sens et la conscience est conçu comme fini; mais, en concevant ainsi des êtres et des faits, nous ne pouvons assigner de limites à l'espace et au temps qui les contiennent.

A côté et à l'occasion de l'idée du fini, apparaît dans l'esprit celle de l'infini, c'est-à-dire de ce qui est sans bornes, de ce qui n'a ni commencement ni fin. L'infini, d'après le mot même, c'est ce qui n'a pas de limites. La première question à se poser, à propos de cette notion, consiste à se demander si nous l'entendons véritablement, si ce mot ne cacherait pas une absurdité. Il faut distinguer deux cas, l'un où on appliquerait cette notion à un objet dont l'existence est posée par ses limites, l'autre où cette notion se contente d'indiquer la suppression des limites dans un objet qui peut exister sans elles.

Dans le premier cas, il est clair que l'attribution de l'infinitude est absurde. C'est le cas de tous les objets mathématiques. Dire d'un triangle qu'il est infini est absurde, car un triangle n'existe que par la position de ses trois cotés qui le limitent; l'affirmer infini, c'est dire à la fois :

1° qu'il a des limites, puisqu'il est triangle;
2° qu'il n'en a pas, puisqu'il est infini.

C'est l'absurdité même. Toute quantité réelle infinie est ainsi absurde et le concept d'un infini de quantité l'est également. En est-il de même de la qualité? Oui, pour certaines qualités qui enferment essentiellement en elles de la quantité. Par exemple, une vitesse infinie est absurde, car la vitesse infinie serait celle où un espace quelconque serait parcouru en un temps nul, mais la formule de la vitesse étant V = E/T , si l'on écrit V= E/0 , ce qui serait l'expression de la vitesse infinie, la formule n'offre plus aucun sens. Le mouvement a disparu de la vitesse et qu'est-ce qu'une vitesse sans mouvement?

Mais il est des qualités comme l'intelligence, la bonté, la force, qui ne sont pas conçues par leurs limites, mais sans lesquelles, au contraire, on ne comprendrait pas les qualités négatives qui leur correspondent.

Les limites de l'intelligence sont l'ignorance et l'erreur. Or, ce n'est pas par l'ignorance, par l'erreur, que nous savons ce que c'est que l'intelligence, c'est au contraire par l'intelligence que nous savons ce que c'est que l'ignorance et l'erreur. Si donc, nous pensons une intelligence sans borne, infinie, c.-à-d. sans ignorance, sans erreur, nous pensons une intelligence pleinement intelligente; nous n'introduisons donc aucune absurdité dans le concept; nous le purifions, au contraire, de tout ce qui, dans l'expérience, peut le contredire et le contredit, en effet.

De même, ce n'est pas par la faiblesse que nous concevons la force (au sens philosophique), mais nous concevons la faiblesse par la force. Une force infinie, une force sans faiblesse, est donc une force qui n'est que force, une force pure, pleinement intelligible. Si on trouve quelque difficulté à concevoir la force infinie, c'est qu'on introduit dans l'idée de force quelque représentation de mouvement et par là de quantité, ainsi qu'on le fait en mécanique où le mot force désigne le produit de la masse par la vitesse. La force pure, ou, ainsi que parlait Aristote, l'acte pur exclusivement qualitatif, ne renferme aucune contradiction, quand il n'est soumis à aucune limitation.

De même, encore, c'est la bonté qui permet de concevoir la méchanceté et non la méchanceté qui permet de concevoir la bonté. Une bonté infinie n'est donc pas absurde, mais, au contraire, pure de toute contradiction. La force, l'intelligence, la bonté sont dites infinies quand on les purifie en les séparant de la faiblesse, de l'ignorance et de la méchanceté qui, dans l'expérience, les bornent et les limitent. Le concept d'infini exprime la manière dont nous arrivons à former ces conceptions; c'est une expression logique.

Il ne faut donc pas confondre la notion mathématique de l'infini représentée par le symbole 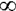et qui est proprement la notion de l'indéfini, avec la notion métaphysique d'infini. (G. Fonsegrive).
-

Différence de l'infini et de l'indéfini

« Nous ne nous embarrasserons jamais dans les disputes de l'infini; d'autant qu'il serait ridicule que nous, qui sommes fini, entreprissions d'en déterminer quelque chose, et par ce moyen le supposer fini, en tâchant de le comprendre; c'est pourquoi nous ne nous soucierons pas de répondre à ceux qui demandent si la moitié d'une ligne infinie est infinie, et si le nombre infini est pair ou non pair, et autres choses semblables, à cause qu'il n'y a que ceux qui s'imaginent que leur esprit est infini qui semblent devoir examiner telles difficultés. Et pour nous, en voyant des choses dans lesquelles, selon certains sens, nous ne remarquons point, de limites, nous n'assurerons pas pour cela qu'elles soient infinies, mais nous lee estimerons seulement indéfinies. Ainsi, parce que nous ne saurions imaginer une étendue si grande que nous ne concevions en même temps qu'il y eu peut avoir une plus grande, nous dirons que l'étendue des choses possibles est indéfinie; et parce qu'on ne saurait diviser un corps en des parties si petites que chacune de ces parties ne puisse être divisée en d'autres plus petites, nous penserons que la quantité peut être divisée en des parties dont le nombre est indéfini; et pas ce que nous ne saurions imaginer tant d'étoiles que Dieu n'en puisse créer davantage, nous supposerons que leur nombre est indéfini, et ainsi du reste.

Et nous appellerons ces choses indéfinies plutôt qu'infinies, afin de réserver à Dieu seul le nom d'infini; tant à cause que nous ne remarquons point de bornes en ses perfections, comme aussi à cause que nous sommes très assurés qu'il n'y en peut avoir. »

(Descartes, extrait des Principes de la Philosophie, I, 26).

L'infini en mathématiques

Infiniments grands.
En termes de mathématiques, une quantité 'variable est dite infinie, ou est un infini, un infiniment grand, quand il est possible de la faire croître au delà de toute limite, de la prendre plus grande que toute quantité donnée fixe. Ainsi une quantité infinie est :

1° essentiellement variable (une quantité fixe très grande n'est jamais infinie);
2° une valeur particulière d'une quantité infinie peut être très petite, nulle par exemple, pourvu qu'on puisse la prendre plus grande que toute quantité fixe donnée, elle sera qualifiée infinie.

Donnons quelques exemples de l'emploi du mot infini : un nombre et le double de ce nombre deviennent infinis en même temps, cela veut dire que quand un nombre peut être pris plus grand que tout nombre donné, il en est de même du double de ce nombre. En ajoutant successivement les deux premiers, les trois premiers, les quatre premiers... nombres, on obtient un résultat infini, cela veut dire que l'on obtient un résultat qui peut dépasser tout nombre fixe donné. Quelquefois le langage prend une forme plus elliptique et l'on dit d'une quantité qu'elle est infinie dans une circonstance donnée : il faut entendre par là qu'elle peut devenir plus grande que toute quantité donnée quand cette circonstance tend à se produire; par exemple, on dit que le quotient d'une division est infini quand le diviseur est nul et quand le dividende est différent de zéro. Il faut traduire cette phrase ainsi en langage ordinaire : en prenant le diviseur suffisamment petit, on petit rendre le quotient plus grand que toute quantité donnée. On dit quelquefois que deux droites parallèles menées par des points fixes A, B, se rencontrent à l'infini, cette phrase n'a de sens que si les droites considérées ne sont pas parallèles; elle doit être traduite ainsi en langage ordinaire: lorsque l'angle des deux droites devient de plus en plus petit, leur point de rencontre se trouve à une distance de A ou B que l'on peut rendre de plus en plus grande de manière à lui faire dépasser toute quantité donnée fixe.

Infiniment petits.
Une quantité variable qui a pour limite zéro est ce que l'on appelle un infiniment petit ou une quantité infiniment petite. Une quantité fixe n'est donc jamais infiniment petite. Zéro lui-même étant fixe n'est pas infiniment petit, mais il peut être une valeur particulière d'un infiniment petit, comme tout autre nombre d'ailleurs. Infiniment petit ne veut pas dire très petit, il veut seulement dire variable, qui a pour limite zéro, ou qui peut être pris aussi petit que l'on veut.

Des divers ordres des quantités infinies et infiniment petites.
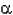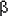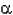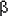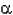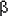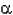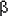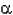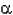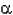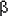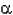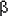Soit une quantité infinie, soit une autre quantité infinie. Si le rapport / tend vers une limite différente de zéro, quand et croissent indéfiniment, on dit que et sont de même ordre. On dit que ^m est d'ordre m par rapport à ; tout infini de même ordre que ^m sera dit d'ordre m. Enfin si croît indéfiniment avec , on dit que est d'ordre supérieur à 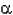, et cela quand même il ne serait d'aucun ordre, c.-à-d. quand même il n'existerait pas de nombre m tel que lim 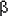/ 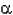^m soit différent de zéro et fini. 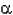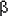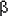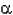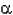De même si est un infiniment petit ainsi que , ces infiniment petits sont dits du même ordre, si / tend vers une limite différente de zéro quand et 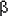tendent vers zéro. 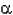^m et les infiniment petits de même ordre que 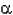^m sont dits d'ordre m par rapport à 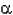; enfin si lim 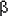/ 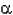est nul, on dit que 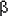est d'ordre supérieur par rapport à 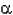, bien qu'il puisse être impossible de lui assigner un ordre déterminé.

Point associés à l'infini.
En géométrie trilinéaire, lorsque les coordonnées barycentriques d'un point sont 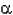, , 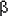, 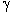le point qui a pour coordonnées 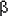-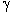, 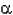- 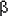est dit associé à l'infini du premier. (GE).

David Foster Wallace, Tout et plus encore : Une histoire compacte de l'infini, Ollendorff et Desseins éditions, 2011.
2918002070

Michel Blay, Penser avec l'infini, Vuibert, 2010.

Joel Biard, De la théologie aux mathématiques : l'infini au XVIe siècle, Les Belles Lettres, 2005. - Au XIVe siècle la croyance en la puissance illimitée de Dieu conduit à un intérêt renouvelé pour l'infini, particulièrement à partir de Duns Scot qui pense Dieu comme étant infini et introduit les raisonnements mathématiques en théologie. Une grandeur ou une multitude infinies sont-elles pensables? Un infini pourrait-il être plus grand qu'un autre? Dieu aurait-il pu faire que le monde soit éternel? Aurait-il pu créer une puissance infinie? Ces questions, et d'autres qui leur sont liées notamment sur la structure du continu, sont posées, discutées et résolues avec des arguments logiques, mathématiques ou philosophiques. Des textes (Bradwardine, Grégoire de Rimini, etc.) sont présentés qui montrent la variété des arguments utilisés et mettent en évidence la progression des discussions. Cet ensemble de traductions a ainsi pour ambition de présenter à un public non spécialiste un aspect de la richesse de la pensée du XVIe siècle (couv.).

Joseph Silk, L'univers et l'infini, Odile Jacob, 2005.
2311001469
En bibliothèque - V. Cousin, Cours de l'histoire de la philosophie moderne, 5 vol. in-12, Paris, 1846, t. IV, 12e leçon.

Dictionnaire Idées et méthodes