Cercle.

-

Cercle. - La définition mathématique du cercle en fait l'ensemble des points situés sur un même plan, à la même distance (le rayon du cercle) d'un point donné (le centre du cercle).

Cercle inscrit, celui dont la circonférence est tangente intérieurement à tous les côtés d'un polygone; le rayon du cercle est appelé souvent apothème du polygone, qui est dit circonscrit au cercle.
Cercle circonscrit, cercle dont la circonférence passe par tous les sommets d'un polygone que l'on dit inscrit dans le cercle.

Les surfaces des cercles sont entre elles dans le même rapport que le carré des rayons; ainsi le rayon devenant 2, 3, 4 fois plus grand, la surface devient 4, 9, 16 fois plus grande.

La surface d'un cercle s'obtient en multipliant le nombre 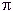(Pi) par le carré du rayon, ce qui s'exprime en posant :

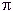S = .R²

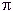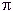Dans cette formule S représente la surface du cercle, R son rayon, et le rapport de la circonférence au diamètre, soit = 3,14159269...

La circonférence du cercle se calcule pour sa part en multipliant le rayon R par 2 :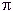

P = 2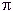.R

Quand on coupe une sphère par un plan, l'intersection est un cercle. Lorsque le plan passe par le centre de la sphère, on a ce qu'on appelle un grand cercle; si le plan ne passe pas par le centre de la sphère, on a un petit cercle.

Dictionnaire Idées et méthodes