Lambert (Johann Heinrich), savant universel né à Mulhouse (alors en Suisse) le 26 août 1728, mort à Berlin le 25 septembre 1777. Fils d'un tailleur protestant que la révocation de l'édit de Nantes avait forcé de quitter la France pour une ville alsacienne où son culte était encore toléré. Lambert étudia à peu près seul, outre les langues anciennes et modernes, presque toutes les sciences, la physique, la mécanique, l'astronomie, la philosophie, et s'exerça même dans la poésie et l'éloquence. Puis ils entra à dix-huit ans, comme secrétaire, à Bâle, chez le docteur Iselin. Il y trouva une bibliothèque qui l'aida à compléter son instruction, et appelé en 1748 à diriger l'éducation du petit-fils du comte de Salis, il redoubla d'ardeur pour se mettre à la hauteur de sa mission. Il commença dès lors à se faire connaître par des articles scientifiques, et, dans les voyages qu'il fit à partir de 1756 avec son élève, entra en relations avec les savants de divers pays. 

En 1769, Johann Lambert obtint un traitement de professeur à Augsbourg et, en 1764, Frédéric Il l'attacha à l'Académie de Berlin dont il fut, jusqu'à sa mort, un des membres les plus actifs et les plus brillants. Il s'y distingua surtout dans les mathématiques et la métaphysique. Lambert a prouvé l'incommensurabilité du rapport de la circonférence au diamètre, a perfectionné les méthodes géodésiques, la théorie des comètes et a trouvé en astronomie un théorème fort simple, qui porte son nom. Lambert fut au nombre des amis de Kant. On signalera aussi parmi les plus célèbres de ses contributions aux mathématiques  sa démonstration de l'incommensurabilité de 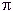(mémoires de 1768), sa conception de la trigonométrie hyperbolique (1770), ainsi que la série qui porte son nom (1772), et qui a été l'objet des travaux d'Euler et de Lagrange. (T.).

Principaux ouvrages - Lambert a beaucoup écrit et sur les sujets les plus divers. Ses ouvrages publiés à part sont : les Propriétés remarquables de la route de la lumière dans les airs, etc. (La Haye, 1758, en allemand; réed.,Berlin, 1773), travail très important qui devait plus tard servir de point de départ à Arago; Die freie Perspective, etc. (Zurich,1759; rééd.,1774), remarquable par le non-emploi du géométral; Photometria (Augsbourg, 1760); lnsiqniores orbitae cometarumproprietates (Augsbourg, 1761) qui, entre autres propositions sur les coniques, contient la formule sur la relation entre le temps employé par un astre le parcourir un arc de son orbite, la corde de de cet arc et les deux rayons vecteurs extrêmes, formules dont l'énoncé est connu sous le nom de Théorème de Lambert; Cosmologische Briefe (Augsbourg, 1761), traduites par Mérian sous le titre de Système du monde (Berlin, 1770), puis par d'Arquier (Amsterdam, 1801); Beschreibung und Gebrauch der logarithmischen Rechentafeln (Augsbourg, 1761 et 1772); Neuer Organon (Leipzig, 1763), ouvrage philosophique encore très remarquable sur la théorie de la connaissance; Beitraege zum Gebrauche der Mathematik (Berlin, 1765, 1770, 1772, 3 vol.); Beschreibung und Gebrauch einer neuen und allgemeinen ekliptische Tafel (Berlin, 1764); Anmerkungen weber die Gewalt des Schiesspulvers (Dresde, 1766); Ueber die Branderschen Mikrometer (Augsbourg, 1769); Kurzgefasste Regeln zu perspektivischen Zeichnungen (Augsbourg, 1768 et 1770); Zusoetze zu den logarithmischen und trigonometrischen Tabellen (Berlin,1770); Anlage zur Architectonik (Riga, 1771, 2 vol., suite importante du Neuer Organon); Beschreibung einer mit calau'schem Wachse ausgemalten Farbenpyramide (Berlin, 1772); Pyrométrie (posth., Berlin, 1779); sa correspondance (Deutscher-Gelehrter-Briefwechsel) a été publiée en 5 vol. (Berlin, 1781-1787) par Jean II Bernoulli. On a de plus, de Lambert, une cinquantaine de mémoires dans le Recueil de l'Acad. de Berlin, et de nombreux articles dans L'Annuaire de Bode, l'Archiv d'Hindenburg, dans le Leipziger Magazin, les Mémoires de l'Acad. de Bavière.